The recommendations in the National Council of Teachers of Mathematics (NCTM) standards documents call for teachers to relinquish their roles as the sole authority in the mathematics classroom to help students build mathematics knowledge through the use of problem solving, to orchestrate classroom discourse in ways that facilitate students’ learning, and to use various tools (e.g., manipulatives, technology) to enhance the learning and teaching of mathematics (NCTM, 1989, 1991, 2000). Although many teachers acknowledge the virtues of the espoused ideas, they may not be readily able to translate ideas in ways that allow them to alter their classroom practices (Cohen, 1990; Eisenhart et al., 1993). In other cases, teachers may take risks but discontinue the use of reform methods because they lack appropriate feedback or support (Carter & Richardson, 1999; Ensor, 2001; Knapp & Peterson, 1995).
Ultimately, teachers may find meeting and addressing the challenges of the reform effort difficult if they do not have markers with which to gauge their level of success after attempting an innovation. Simply stated, the standards documents encourage teachers to teach mathematics in ways that many of them have not experienced firsthand. As a result, they have to imagine a classroom they may have never witnessed. In fact, for many teachers the classroom environments and interactions encouraged in the standards are a far cry from the kinds of experiences they had as students. Therefore, it becomes important to engage teachers in activities requiring them to examine what it means to learn and teach in environments encouraged by the reform effort (Loucks-Horsley, Hewson, Love, & Stiles, 1998; Smith, 2001).
As mathematics teacher educators, we have grappled with ways to help elementary teachers create a vision for a standards-based classroom as they examine their content knowledge and their beliefs about learning and teaching mathematics. One major difficulty is that preservice teachers are wary of the innovative methods introduced in methods courses, especially when they have not seen them applied in schools. Typically, preservice teachers enter teacher education programs with pre-existing notions about mathematics classrooms. This may be a result of what Lortie (1975) referred to as the “apprenticeship of observation.” In other words, they believe that the mathematics instruction they have observed as students represents how mathematics instruction should be delivered.
Many teacher education programs incorporate the use of field experiences to help preservice teachers begin to learn what it means to teach. Although the benefits of these experiences are many, they can also be problematic. For example, preservice teachers may be in placements that do not support or encourage the ideas suggested by the reform effort. In fact, although preservice elementary teachers at our institutions are often involved in field-based experiences throughout their teacher education program, at the elementary level there is no guarantee that they are observing teachers as they teach mathematics. As a result, it has been difficult to help teachers create a vision for (a) the depth of understanding that can be developed when students are given opportunities to explore mathematics topics in an active way, and (b) the implementation of innovative mathematics activities or teaching strategies with an actual group of students.
In particular, individuals without “profound understanding of fundamental mathematics” (Ma, 1999) find exploring mathematics from the conceptual basis difficult. As a result, they believe it would be difficult for pupils to investigate topics on their own, to reason mathematically, and to present their ideas to their peers. They, in effect, cannot envision a classroom where students are encouraged to work together to develop and share multiple strategies and where authority for mathematical knowledge is shared with the students and not relegated to the teacher.
Online Video as a Source of Reflection for Preservice Mathematics Teachers
This article describes our attempt to combat years of “apprenticeship of observation” by requiring preservice teachers to observe mathematics classrooms that are closer in alignment to the recommendations of the standards than what they may have experienced. No claims are made about the long-term effects of using online videos nor is our rationale for using them directly connected to research findings. Instead, this article describes how and why we have incorporated the use of these videos in our elementary methods courses and describes the reflections of elementary preservice teachers after viewing selected videos. Specifically, the ways online videos are used to encourage preservice teachers to examine their beliefs about how students learn mathematics and what it means to teach mathematics are discussed. With the help of readily available online videos, preservice and in-service teachers can be provided opportunities to examine classrooms that have successfully implemented many of the ideas espoused in the standards.
First, approaches will be described that were used with preservice elementary teachers. Then, preservice elementary teachers’ reflections after viewing a particular video are shared. Finally, some of the challenges of incorporating online videos into an elementary methods classroom are discussed.
Using Online Videos in Elementary Methods Courses
Currently, there exist many sources of videos that can be used to help teachers examine mathematics teaching and learning (e.g., video tapes, video discs; Friel & Carboni, 2000). These videos can be used in various ways; however, they typically require facilitation by an instructor during face-to-face interaction. For example, in an elementary methods course, instructors can show the Cognitively Guided Instruction (CGI) classroom videos during a course session and engage students in a discussion related to teaching and learning (Carpenter, Fennema, Franke, Levi, & Empson, 1999). However, this structure may require that (a) the instructor has access to a copy of the commercially available videos, and (b) the instructor uses class time to show the videos and facilitate the class discussion. Although important and useful, both of these activities require the use of in-class time that may limit opportunities to engage in other activities.
Because each of our classes includes many activities we deem important and do not want to eliminate, we opted to use videos that are accessible on the Internet. This accessibility allows the incorporation of video in our courses without consuming limited class time for viewing them. Additionally, preservice teachers may view these videos at a time convenient for them, and the conversation is extended beyond established class time. It also provides preservice teachers an opportunity to reflect upon the material and add to their discussion at their own pace. To that end, we opted to use PBS Mathline videos, although we acknowledge that others exist (see the appendix).
We use PBS Mathline videos for the following reasons. PBS Mathline provides searchable videos of mathematics teaching and learning at each of the grade bands K-2, 3-5, 6-8, and 9-12. (Editor’s note: See the Resources section at the end of this paper for a list of website URLs.) The videos of mathematics classrooms found at this site address a wide variety of topics, including numeration, computations, algebra, geometry, measurement, and problem solving. Furthermore, each broad topic is further categorized according to more specific mathematics topics. Individuals may view a clip (a small segment of the lesson), watch the entire lesson, and read the lesson plans for the observed lesson. In addition to whole class interactions, some of the video segments include small group or one-to-one interviews with students to reveal their understanding about particular mathematics topics. Other video segments include teacher reflections about changes in instruction and goals for the lesson.
Video Assignments in Elementary Methods Courses
The focus of our courses is to offer teachers many opportunities to engage in and examine the teaching of mathematics using various methods (e.g., discovery learning, cooperative learning, alternative assessments) and various tools (e.g., manipulatives, technology). Class time is spent exploring mathematics conceptually and discussing the practical implementation of such activities by examining the roles of the teacher and students in such settings. Overall, the goal is to familiarize preservice teachers with the recommendations in the NCTM (2000) Principles and Standards for School Mathematics and provide them opportunities to experience teaching and learning that adhere to these standards.
Several assignments are given to help prospective teachers reflect on their potential role as teachers. Viewing and reflecting on online videos represents one such assignment and accounts for approximately 10% of the course grade. Preservice teachers are required to view several PBS Mathline videos that highlight ideas presented in our methods courses (e.g., use of technology, classroom discourse). They are asked to view the entire lesson and contribute to a discussion about what they observed. The goal of this assignment is to have preservice teachers view various mathematics classrooms so they can identify the characteristics that make them effective, to examine the reasoning of students, and to begin to consider and examine those behaviors they may emulate; thus, the videos provide alternatives to traditional mathematics classrooms they have experienced or observed.
The expectation is that, while viewing the video lessons, preservice teachers reexamine their deeply held beliefs regarding what it means to learn and teach mathematics. A secondary purpose for requiring preservice teachers to view these videos is to make them aware of a resource they can use for ongoing professional development once they complete the teacher preparation program.
The PBS Mathline site contains many videos that address precise aspects of both NCTM content and process standards for grades K-12. For our viewing assignments, we each select specific videos to support ideas addressed during the course. For example, while the topic of problem solving is being covered, a video depicting the use of problem solving in the classroom would be assigned.
Although we share a common view regarding the use of online videos, the implementation at our respective institutions differs. Kellogg teaches at a private liberal arts college that has a network designed to facilitate creating websites to accompany courses (see Figure 1). His methods classes usually average from 10 to 16 preservice teachers each semester, providing opportunities for all to participate in class discussions. Typically, six online videos are assigned for viewing throughout the semester to complement course content and address specific NCTM (2000) standards, including such topics as assessment, technology, number and operations, algebra, geometry, measurement, data analysis, and problem solving.
For example, while discussing alternative assessment, the preservice teachers are asked to complete Web Video Assignment #2 by viewing the online video Bead-Dazzling (click on “Watch Entire Lesson”). This video shows a teacher interviewing students in real time. To accomplish this assignment, the students log into the course website, and proceed to click on the “Web Video 2” link in the “New Announcement” portion of the web page. After clicking on that link, a page opens with general instructions about viewing the video and what mathematical content will be addressed (for example, see Figure 2). The preservice teacher then simply clicks on the appropriate link found in the “Manage Links” portion of the same Course Website.
After viewing the online videos outside of class, preservice teachers are asked to complete a form to help initiate class discussion and promote personal reflection. They are asked to list ways in which the teacher’s actions and the activities offer students opportunities to experience standards-based instruction. Additionally, preservice teachers are asked to provide evidence of student behaviors indicating that the goals of the standards are being realized. During the next class session, the preservice teachers are engaged in a discussion of the video assignment.
In contrast, Kersaint teaches at a large public research institution where Blackboard, a web-based tool to help the instructor make instructional material available to course participants, is provided to facilitate online discussion. Thus, she has the infrastructure to post information online, allowing preservice teachers to link to videos directly from the course and to respond to an online discussion about the viewed lesson. The class size for an elementary methods course is typically 35 preservice teachers, which impacts the amount of class time that can be devoted to extended discussion about the videos. As a result, the discussions of the videos are relegated to ongoing conversations using the discussion board outside of class time.
In her course, preservice teachers are asked to view videos that address the following content areas: problem solving, numbers and number sense, fraction concepts, and proportions. (The preservice teachers in this case are taking the first course in a two-part elementary mathematics methods course sequence. The first course focuses on number concepts and operations. The second course deals with geometry, probability, and data analysis. Algebra is addressed to some extent in both courses.) However, the discussions typically address the process standards observed. In most cases, preservice teachers are presented with options they can view at each of the levels—K-2 and 3-5. For each of the lessons viewed, preservice teachers are required to (a) identify the lesson that was viewed and indicate how (and what) NCTM standards are being implemented; (b) describe how the viewed lessons differ from the mathematics lessons they have participated in or have observed; and (c) describe what they have learned about becoming a mathematics teacher from viewing the videos.
Additionally, preservice teachers are given the option to discuss other important issues that were not addressed in the three categories identified. For example, they often discuss how the class was organized (e.g., classroom management). To encourage dialogue, they are required to respond to comments provided by at least two of their peers. This requirement has resulted in ongoing discussion, as preservice teachers reply to comments provided about their particular reflections.
Preservice Elementary Teachers’ Reflections
After viewing these online videos, preservice teachers in each of our courses have commented that it is helpful to view the ways teachers apply the reform recommendations that they studied in the methods class. The videos help validate the instructional approaches presented in the course, as well as present mathematics in an intriguing manner. In fact, preservice teachers often report that they learn mathematics while viewing the videos. For many, the online videos provide their first exposure to standards-based mathematics instruction, and their responses have been positive.
To view the video prior to reading the reflections of preservice teachers, go to To Half or Half Not and click on “Watch entire lesson.” This particular video was assigned toward the latter part of Kersaint’s course after the preservice teachers had opportunities to discuss pertinent mathematics content and pedagogical issues related to developing students’ conceptual understanding of rational numbers. The preservice teachers reacted to the lesson and described how the NCTM standards were reflected in the lesson. For this particular assignment, preservice teachers were given great flexibility regarding the nature of their responses.
Individual teachers focused on different aspects of the mathematics classroom as they viewed the lesson. (All names used are pseudonyms.) Some reacted to the global features of the lesson:
This video shows just how much fun you can have with math and that you don’t need to just place a worksheet full of fractions in front of your students. (Tristen)
The children seemed to feel confident and enjoyed the activity a lot. This activity provided students with a very neat way to understand fractions and it stimulated interest in the topic. (Kelly)
Other preservice teachers discussed particular components of the lesson, such as the use of multiple representations, the use of writing in the mathematics classroom, or the use of real-world applications.
Multiple representations:
- By seeing the different ways that one slice can be made into two equal parts or by using the…geoboards they [the students] are able to notice that a shape is not required to stay in one aspect of view. When you ask them to cut a square in half they most likely have one line of symmetry in mind but by demonstrating the different possible ways he [the teacher] opened their thinking the next time they face a similar task. (Kelly)
Writing in the mathematics classroom:
- I also liked the way that he asked the students to write a letter to the customers about the problems with the ribbons. This gave the students a chance to practice their writing skills as well as an opportunity to practice communicating their mathematics understanding. (Ken)
Real-life applications: “I liked how this teacher incorporated a real life situation into a math problem” (Tristen).
Still other preservice teachers focused on the teacher’s behavior and commented on his rationale for teaching the way that he did and the students’ engagement in the process of learning.
Allowing students to explore mathematics:
- It also caught my attention when the teacher said that he rarely gives the students answers. That he just lets them figure it out on their own. I think this is something that I really need to work on. When I am working with a student I am so tempted to tell them that they have the answer right or that it is wrong, etc. I want to cut in and finish their sentence or complete their thought and show them how to do the problem. I know that I really need to work on being patient and hold my tongue and let the student figure things out on his own. (Ken)
- The students were asking questions among themselves and not relying on the teacher to give the answers. They were actively engaged in the learning process. (Stan)
- The children were very creative in figuring out how to make halves without duplicating the work of other children. (Bob)
- By having students reason and justify their answers they were really required to think about what they were doing. (Karen)
Student presentations and communication:
- The students had to orally explain their ideas to the class and the reasons for what makes something half. They eventually discovered that the two parts had to be equal, without being told by the teacher. Then a student reasoned that the line dividing the halves did not have to be straight, as long as the pieces were the same size. (Nicole)
- It was a creative way to get the children to see how many different ways they could show 1/2. It got the children to communicate their understanding about fractions. It was fun for the students and it can help the teacher assess which students understand the concepts. (Kamara)
Questioning: “I like the idea that he asks a lot of questions to get the students engaged in the lesson” (Freda).
Use of manipulatives:
- I had no idea what geoboards were when we began this class. Learning about manipulatives and what a powerful tool they can be in reaching students and enabling them to understand and explain math concepts has really made me think about other day-to-day objects that could also be used as manipulatives. It was also exciting for me to see a young teacher in a position using creative and exciting ways to teach math. (Danielle)
Others reflected on their own experiences as learners of mathematics:
- When I learned fractions, I had thought to myself, “When will I have to use these?” But the teacher did a marvelous job showing the students and having them act out various situations that do use fractions. I liked how the teacher cut out the bread into the halves. The students explained also. I was getting stumped for a bit after he asked are there any other ways to cut the bread in half because I had never thought to cut a zigzag in the bread. But as long as both parts of the bread were equal it worked. (Daria)
- This type of classroom setting was very different than when I learned fractions. We did not play any games. We just worked from the textbook. I learned from this video to be creative when teaching mathematics. This makes it more fun for the students to learn math and they are more interested in learning. (Nevia)
The comments provided by the preservice teachers reveal how they began to examine key aspects of mathematics teaching and learning. In fact, they were commenting on methods that many initially thought were impossible to do with students. Moreover, several preservice teachers reported that they viewed other videos that were not assigned and looked forward to viewing more.
Instructors’ Reflections
Prior to using these videos, the instructors agreed that they faced a higher level of resistance regarding the use of reform methods than presently occurs. Although the preservice teachers typically engaged in activities that were part of the course, the level of reflection regarding such activities was lacking. Preservice teachers often assert that many of the discovery approaches used would be difficult for students, particularly when they themselves found the pertinent mathematics challenging. This often meant that they rejected the possibility of using such approaches. However, after viewing the videos of students doing mathematics, talking mathematically, and presenting their findings, preservice teachers are more able to understand alternative approaches and consider their use.
Class discussions about course activities, as well as possible students’ responses to those activities, have always been incorporated into our elementary mathematics methods courses. However, we find that preservice teachers respond differently when they are able to make personal connections to the content presented in the online videos. Rather than making claims about what may or may not be possible in the classroom, the conversation has shifted to include what needs to occur to help facilitate reform recommendations.
Although preservice teachers’ reflection improved in both courses, there was a marked difference in the level of reflection provided by the preservice teachers in the two courses. One possible explanation for differences in teachers’ reflections could be the method used to facilitate the discussions: in class vs. online format. During in-class discussions, preservice teachers may be reluctant to share their perspectives regarding a topic or occurrence because of immediate reactions by peers with opposing views. Some may find their peers’ emotional or passionate responses stifling. Additionally, reticent individuals may not contribute to the class discussion because other more vocal individuals may dominate the discussion.
In contrast, using the online discussion board gives every preservice teacher an opportunity to reflect and share his or her point of view. Kersaint finds that preservice teachers who are reluctant to participate during in-class discussions often provide insightful comments during the out-of-class, online discussion. Using an online discussion board enables individuals to share thoughts and comments that they may generate long after a particular discussion or in reaction to something someone had written but they had not originally considered (see McDuffie and Slavit, 2003, for an extended discussion about the potential that discussion boards provide). No matter the format, discussions are an important aspect of incorporating online videos into elementary methods courses.
Thus far, this article has focused primarily on sharing the potential benefits of using online videos. However, as we refine the implementation of online videos in elementary methods courses, we have had to address several challenges. For example, the availability of appropriate technology is often an issue. In early implementation, preservice teachers with only dial-up Internet service attempted to view the videos at home. However, a high-speed Internet connection is necessary to view the streaming video contained in the video clips. Consequently, preservice teachers have been encouraged to view the videos on campus. Additionally, problems with campus networks can wreak havoc with individuals trying to access the video assignments, especially when deadlines are involved.
Other issues extend beyond the technology or format used for discussion. As an example, should teacher educators establish the context for viewing a video prior to asking preservice teachers to view it or should preservice teachers be asked to view the videos without such contextual information? The former may lead preservice teachers to respond in ways they perceive are expected by the instructor. In contrast, in the latter approach preservice teachers may not make anticipated links. A related issue is the placement of videos in the sequence of course activities. Should the video be used to introduce specific concepts that will be addressed or should the video be a culmination of previous interactions? Which approach might result in improved reflection? With each question we pose, we find that there are other related questions to be addressed.
Although we do not claim to have all the answers to these questions, we do feel strongly about the use of such videos in our courses. We find that preservice teachers are attentive and reflective in class because they see the application of course topics taking place in classroom settings. Although instructors may identify videos that suit their own particular purposes, the use of online videos seems most appropriate when the videos are selected to support specific teacher development activities and reflection is facilitated in some way.
Embedding these videos as part of elementary teachers’ preservice mathematics education has helped them appreciate alternatives to traditional methods for learning and presenting mathematics ideas. The intent is not for preservice teachers to blindly emulate the behaviors of the teachers they observe, but instead to examine the type of learning possible when students are asked to engage in mathematics, to reason mathematically, and to communicate their ideas to their peers. The online videos offer an accessible and affordable learning experience, which lends itself to discussion and reflection.
References
Carter, R., & Richardson J. (1999). Dilemmas of constructivist mathematics teaching: Instances from classroom practice. In B. Jaworski, T. Wood, & S. Dawson (Eds.), Mathematics teacher education: Critical international perspectives (pp. 69-77). Philadelphia, PA: Falmer Press.
Carpenter, T. P., Fennema, E., Franke, M. L., Levi, L., & Empson, S. B. (1999). Children’s mathematics: Cognitively guided instruction. Portsmouth, NH: Heinemann.
Cohen, D. K. (1990). A revolution in one classroom. The case of Mrs. Oublier. Educational Evaluation and Policy Analysis, 12, 327-47.
Eisenhart, M., Borko, H., Underhill, R., Brown, C. Jones, D., & Agard, P. (1993). Conceptual knowledge falls through the cracks: Complexities of learning to teach for understanding. Journal for Research in Mathematics Education, 24, 8-40.
Ensor, P. (2001). From preservice mathematics teacher education to beginning teaching: A study in recontexualization. Journal for Research in Mathematics Education, 32, 296-320.
Friel, S. N., & Carboni, L. W. (2000). Using video-based pedagogy in an elementary mathematics methods course. School Science and Mathematics, 100, 118-127.
Knapp, N. F., & Peterson, P.L. (1995). Teachers’ interpretation of “CGI” after four years: Meaning and practices. Journal for Research in Mathematics Education, 26, 40-65.
Lortie, D. C. (1975). Schoolteacher. Chicago: The University of Chicago Press.
Loucks-Horsley, S, Hewson, P.W., Love, N., & Stiles. (1998). Designing professional development for teachers of science and mathematics. Thousand Oaks, CA: Corwin Press.
Ma, L. (1999). Knowing and teaching elementary mathematics. Mahwah, NJ: Lawrence Erlbaum.
McDuffie, A. R., & Slavit, D. (2003). Utilizing online discussion to support reflection and challenge beliefs in elementary mathematics methods classrooms. Contemporary Issues in Technology and Teacher Education [Online serial], 2(4). Retrieved March 19, 2004, from https://citejournal.org/vol2/iss4/mathematics/article1.cfm
National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (1991). Professional standards for teaching mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
Smith, M.S. (2001). Practice-based professional development for teachers of mathematics. Reston, VA: National Council of Teachers of Mathematics.
Other Sources & Online Videos
MMM — The Modeling Middle School Mathematics
“Modeling Middle School Mathematics is a professional development program using video lessons and Web-based Internet materials to examine each of the five NSF-funded middle school math initiatives: Connected Mathematics, MathThematics, MathScape, Math in Context, and Pathways” (MMM, 2003; http://www.mmmproject.org/video_matrix.htm). In addition to other information, this site contains video clip examples from each of the curricula. The clips address a variety of ideas, including student/teacher discussion, student activity, student dialogue, student work, student presentations, group work, group discussion, interviews with teachers using the materials and their reflections.
FCAT Staff Development Tools
This staff development tool is a program that was developed to help teachers prepare students for Florida¡¯s high stakes assessment, the Florida Comprehensive Assessment Test. Regarding mathematics, two sites were developed, one at the 5th grade level and one at the 8th grade level. Each of these sites includes video of Florida teachers teaching mathematics.
FCAT 5th Grade Math (http://www.fcit.usf.edu/FCAT5m/DEFAULT.HTM)
FCAT 8th Grade Math (http://www.fcit.usf.edu/FCAT8m/DEFAULT.HTM)
PBS Mathline – http://www.pbs.org/teachersource/math.htm
Grades K-2 – http://www.pbs.org/teachersource/mathline/lessonplans/search_k-2.shtm
Grades 3-5 ¨C http://www.pbs.org/teachersource/mathline/lessonplans/search_3-5.shtm
Grades 6-8 ¨C http://www.pbs.org/teachersource/mathline/lessonplans/search_6-8.shtm
Grades 9-12 – http://www.pbs.org/teachersource/mathline/lessonplans/search_9-12.shtm
Author Note:
Matt Kellogg
Clearwater Christian College
Email: [email protected]
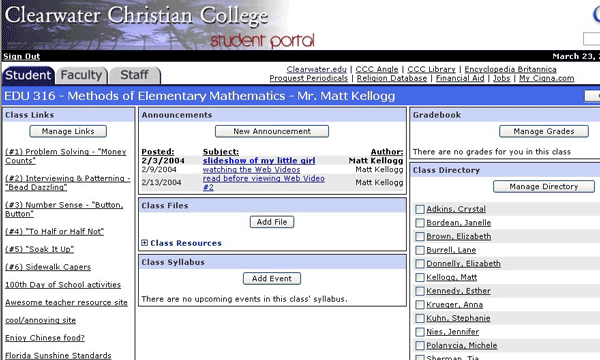 Figure 1. Screenshot of Kellogg’s website.
Figure 1. Screenshot of Kellogg’s website.
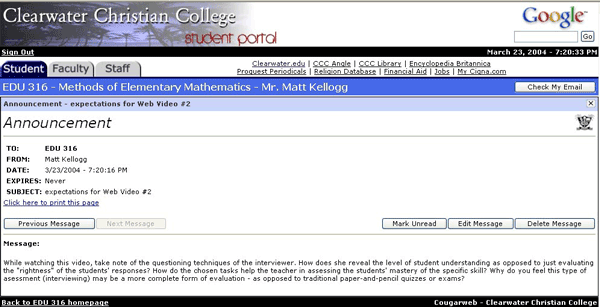 Figure 2. Screenshot of Kellogg’s assignment to watch the Bead-Dazzling video.
Figure 2. Screenshot of Kellogg’s assignment to watch the Bead-Dazzling video.
![]()