The phrase “technologies of writing” was coined at Harry Ransom Humanities Research Center (2005) at the University of Texas at Austin. The term does “not refer to the script alphabet, the calligraphic or marking system that a text employs, but to the practical methods by which these systems are applied — pencil, brush, quill, ink, paint, print, machine key and pixel — and to the material surfaces and sites of the writing itself — clay, animal skin, parchment, linen, wood pulp and cyberspace” ( p. 1). These methods, systems of application, and material surfaces have been changing throughout the years. The tablet PC (sometimes referred to as tablet) is one modern example making changes to all three of these areas.
Tablets have come a long way from once being made of smooth clay or papyrus. Some of the oldest tablets of this nature date back to 3000 BCE and still exist due to their kiln-dried hardening process or resilient inks. At that time a stylus was used while the clay was still wet to make wedge-shaped letters called cuneiform, from the Latin cuneus- (wedge) and forma- (shape). The stylus, tablets, and application process of today’s digital tablets are transformed by technology to being much different for recording thoughts.
Many of the convertible laptops, slates, and tablet PCs in use today have a stylus-based input and navigation system. These newer mobile technologies employ digital ink technology by way of the stylus. Inking is the ability to scrawl (i.e., to write or draw awkwardly, hastily, or carelessly) directly on the screen of a tablet PC or convertible laptop with a stylus, much like writing on a sheet of paper with a pen. The main difference is that the inking method uses pixel imaging and the surface is the screen, or in other words, the digital image of the document.
Digital ink technology is changing the way students can take notes in a course, as well as the teaching methods that an instructor can use to modify the notes to enhance learning. The capabilities of digital ink technology go beyond that of paper and pencil for both the student and the instructor. Students have the ability to write on electronic documents and save their inkings to the document. They also are able to convert their handwritten ad hoc notes to text and orient that converted text into the original document. The text, possibly a meld of handwritten and original text, is fully searchable. This offers students a way to take digital notes during class, review and search through them later to reinforce understanding and, thus, improve memory retention. Instructors are able to supplement their prepared notes by capturing writing, drawing, pointing, annotating, and highlighting that occurs during or after the class presentation. Instructors are also able to produce more interactive learning possibilities in their notes.
One recent study using the tablet PCs to teach a programming unit recognized the importance of learning through a social environment and emphasized active engagement of the learner. Tutty and White (2006) argued that the tablet classroom environment is “more effective than the traditional format of lectures/tutorials/practicals in part due to the increased emphasis on the social aspects of learning and the processes students undertake when meaning making” (p. 4). They went on to conclude that “tablet classrooms enable a more appropriate balance between the duality of participation and reification … and so the negotiation of meaning and learning was also correspondingly greater” (p. 4). The impact of this technology is new, and more studies need to be done about the impact it is having on teaching and learning from the perspective of both the student and the instructor.
This paper is the result of a developmental research project involving a cyclic process of thought experiment (i.e., consideration) and educational testing. In this process the thoughts of the designer about the instructional materials are tested in an actual classroom. Materials developed are not left unchanged; they are constantly revised and improved. The object of the research is the development and testing of the instructional materials, but only as a means to an end (deLange, Burrill, Romberg, & van Reeuwijk, 1993; Gravemeijer, 1994). Observation of the presentation of the lessons, reflections on these observations, and student surveys are used to explore and answer the research questions.
This paper presents the survey results in hopes of answering one of the developmental research project’s questions: How do students perceive the use of digital ink technology for teaching and learning? The project focuses on improving the use of this feature of tablet PCs in order to increase discourse and justification of answers in a mathematics methods course.
Methodology
Participants
The participants in this study were members of two successive cohorts of college students completing a bachelor of arts degree in the elementary education program of a small, liberal arts, 4-year institution. The preservice teachers at this accredited institution of higher education move through this program as a cohort or group of students, taking all of their coursework together. One semester prior to their professional semester, which constitutes the capstone experience in the preparation of teachers and includes a full-time student teaching experience, the students enroll in three methods courses. At the beginning of this semester, students in the cohort are assigned a tablet PC to use. They are free to use this tablet PC in all of their coursework that particular semester, as well as take the tablet with them wherever they may go.
The participants in this study had limited exposure to digital ink technology prior to receiving their tablets. A survey of both cohorts reported that most students had seen this technology in grocery stores on signature machines for credit cards, Palm pilots, and other PDA devices. For all students except 1 out of the 36, however, the introduction to stylus-based digital ink input and navigation on a convertible laptop, tablet, or slate was completely novel.
Materials
A survey instrument entitled, Perceptions of Digital Ink Technology (PDIT), was developed by the researcher (see Appendix A). To establish content validity, the initial survey instrument was examined by a panel of two other instructors teaching with digital ink instructional technology. The panel suggested several wording changes and provided two additional questions to add to the survey. All of the recommendations of the panel were addressed, and changes to the survey were made. Cronbach’s index of internal consistency of the items was 0.877. This coefficient alpha suggests that the scale scores of the survey items are reasonably reliable for participants similar to those in the study (Green, Salkind, & Akey, 2000).
Design and Procedures
Sixteen of 20 students in the fall cohort and 20 of 20 students in the spring cohort were surveyed using the revised instrument two thirds of the way through the semester in which they were assigned the tablet PCs. Consent was obtained and the students were told that neither their participation in the study nor the evaluation of the survey would impact their course grade. There was no missing data, and 36 of 40 students in the two cohorts completed the survey.
Simultaneously throughout the developmental research project, the researcher was designing materials and methods capitalizing on the use of the digital inking capabilities of tablet PCs. Nine different types of effective high-quality inking practices thought to improve instructor-learner dialogue were employed as follows:
1. Controlling an active learning environment. Students inked on prepared notes and examples then shared and justified their responses on the view projector’s screen via a Komatsu AirProjector wireless presentation server and an AirProjector Moderator facilitated by AirProjector Client Software. This system of hardware and software allowed the instructor to get real-time capture of any of the students’ wireless tablet PCs that joined the moderated session. The software has the capacity to create a snapshot or real-time capture of whatever is on the PC’s screen and project it on the view projector’s screen. The instructor, as moderator of the session, controlled the projecting rights of the view projector. Students also came up and inked the justifications of their responses on the instructor’s projected notes via a Smart Classroom’s Sympodium screen.
2. Assessing for Instructional Decision-making. Concurrent and preformative assessments for instructional decision-making were employed using the inking features of the tablet. Several matching, multiple-choice, and short-answer assessment items, along with mathematical performance tasks and discrepant events were used in the course to reveal students’ prior knowledge, instantaneous understanding, naïve conceptions, and misconceptions of mathematical concepts. Various student responses to these items were projected on a whiteboard accompanied by discourse centered on verbalizing the knowledge the students brought to the learning opportunity.
Appendix B highlights a specific example in which the instructor was able to assess the individual student’s level of geometric thinking according to the van Hiele theory (Battista, 2007) based upon their inked responses to preformative assessments. As the instructor viewed the work of several students, inconsistencies in the inked responses helped to identify their misunderstandings about necessary and sufficient conditions for geometric definitions. Thus, the information received from displaying several inked responses can be used by the instructor for identifying inconsistencies, making instructional decisions, and drawing the students’ attention to the valuable decision-making information provided by each of the assessment items.
3. Drawing attention for learners. Visual cues included highlighting or drawing circles around text in prepared notes, adding ad hoc notes in the white spaces, and connecting thoughts shared in the prepared notes.
4. Demonstrating solution strategies and thinking processes. Problems incorporated in the course required students to present and explain their solution strategies or explain their thinking processes by making them visible via digital ink. Some problems required a geometric approach, while others required some type of mathematical or physical representation to find a solution. These problems often required multiple steps to arrive at a solution.
5. Refining thinking processes. Some problems posed in the course required mathematical thinking that was not directly accessible to most students. However, as students built upon the incomplete individual thinking processes demonstrated on the tablets, the group eventually arrived at better, more refined, thinking processes. Appendix C is an example in which the students were given a task to develop an algorithm for finding the area of any polygon on a geoboard. To test the robust nature of their algorithm they were given nine different polygons with which their algorithm should be confirmed. The projection system supported sharing and discussing the various inked solution strategies, as well as the specific cases for which their algorithms were either successful or unsuccessful. Examples and counterexamples using the inking and projection system helped students to identify the flaws in their invented algorithms.
If students reached a point at which they felt their algorithm worked all of the time, the instructor was also able to project a specifically challenging problem to further promote refinement of students’ thinking processes. The challenge problem required a test of the invented algorithms to find the area of a concave polygon like the one shown in Figure 1. As students employed a chop-strategy algorithm the inkings helped them build a recursive (outside-to-inside) strategy, which served as a guide for students who were close to verbalizing the idea of recursion in the chop-strategy algorithm. As shown in Appendix C students were able to break the figure apart, put the relief polygons onto other geoboards and apply the chop-strategy. Coloring the various parts of the relief polygons—both while on separate geoboards and when highlighted on the original geoboard—further helped to refine students’ thinking about the chop-strategy and opened avenues for exploring Pick’s Theorem and the Interior Triangles algorithm.
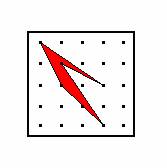
Figure 1. Concave polygon used as challenge problem in finding area algorithms.
6. Coming to a collective/collaborative understanding. A class discussion would often start out having many branches and directions, but the process of selecting and weeding out other options and directions displayed on the digital tablets typically led to consensus as group members convinced one another to think in one way.
7. Capturing in-class spontaneous and dynamic expositions. Students and the instructor frequently created white space in documents to provide room for spontaneous on-task inking. Sometimes additional mathematics instruction was needed for students to arrive at a justified response or to further explore random examples until systematic examples were achieved enabling students to have a better feel for the problem.
8. Creating collective lists of shared ideas. Students were often given some time individually and in small groups to create a list collectively or respond to divergent high-level questions. They inked their ideas below the prompt on their tablet PCs. After adequate time, the groups would select one person to act as a representative and share the group’s combined list with the class on the view projector’s screen. Items surfaced during the whole-group discussion were then added as new ideas in a different-colored ink than their original by students not previously listing these items.
Appendix D shares an example in which students were asked to identify possible geometric objects that might cast the shadow they witnessed when the instructor hid the actual object behind a cardboard screen and subjected the object to the projector’s lamp. The sample shows a student’s original list of possibilities in blue, and a master list in red ink representing the shared ideas of other students in the class. The potential for such a list goes beyond permitting a sense of ownership over the list, as an individual student can see his or her contributions added to those of others in the class and open for comparison. The instructor is able to take the information gathered and determine next steps for further exploration.
9. Marking-up and returning an electronic assignment. Students submitted drafts of lesson plans, journals, and homework assignments to instructors to obtain feedback by way of digital inking directly on the document. These inkings were saved on the document, and then the document was e-mailed back to the student. The benefit of this type of mark-up was that the comments could not just be accepted as with the Track Changes tool option in Microsoft Word. Students had to go back to the original document, make decisions about which changes they were going to make, and then make the changes.
The aforementioned environment and types of effective high-quality inking employed during the study were constantly entering cycles of revision. They were implemented, revised, and implemented again with the goal of improving the instructor-learner dialogue. The participants in the study were surveyed about their perceptions of the use of digital ink technology for teaching and learning.
Data Analysis and Findings
Initially, preservice teachers (N = 36) from two cohorts were to make a “yes” or “no” judgment about each of the 12 items on the survey. Next, they responded to a 7-point Likert-type item rating the degree of their response (see Figure 2 for an example question).
Example:
Did you find the use of projected notes with student inking capabilities helpful? Y / N
Rate the degree of helpfulness. 1 2 3 4 5 6 7
not helpful very helpful
Figure 2. Example question from the Perceptions of Digital Ink Technology survey.
The preservice teachers’ responses to each item on the survey are summarized in Table 1. A p-value of 0.05 was used with a one-sample t-test to compare the mean of each item to a neutral response of 4.0 on the Likert-type scale (i.e., the test value). A response above 4.0 would indicate more positive perceptions with the item (Green et al., 2000). All of the items were found to be significant at the 0.001 level, indicating positive perceptions with all of the items on the survey. The effect size evaluates the degree that the mean scores on the test variable differ from the test value in standard deviation units. If the effect size equals 0, the mean of the scores is equal to the test value, but as the effect size becomes larger it is clear that the mean of the scores is different from the test value. Traditionally, effect sizes of 0.2, 0.5, and 0.8, respectively, represent small, medium, and large effect sizes (Green et al., 2000). In this study, all values for effect sizes exceeded 0.8 (see Table 2).
Table 1
College Student Perceptions of Digital Ink Technology Items (N = 36)
| Item | Likert-Type Scaled Scores N (%) | ||||||
| 7 | 6 | 5 | 4 | 3 | 2 | 1 | |
| Q1 | 9 (25.0) | 10 (27.8) | 15 (41.7) | 2 (5.6) | 0 (0.0) | 0 (0.0) | 0 (0.0) |
| Q2 | 4 (11.1) | 14 (38.9) | 7 (19.4) | 7 (19.4) | 3 (8.3) | 1 (2.8) | 0 (0.0) |
| Q3 | 6 (16.7) | 19 (52.8) | 7 (19.4) | 4 (11.1) | 0 (0.0) | 0 (0.0) | 0 (0.0) |
| Q4 | 7 (19.4) | 12 (33.3) | 13 (36.1) | 4 (11.1) | 0 (0.0) | 0 (0.0) | 0 (0.0) |
| Q5 | 14 (38.9) | 5 (13.9) | 8 (22.2) | 5 (13.9) | 3 (8.3) | 1 (2.8) | 0 (0.0) |
| Q6 | 9 (25.0) | 13 (36.1) | 8 (22.2) | 5 (13.9) | 1 (2.8) | 0 (0.0) | 0 (0.0) |
| Q7 | 4 (11.1) | 10 (27.8) | 13 (36.1) | 7 (19.4) | 2 (5.6) | 0 (0.0) | 0 (0.0) |
| Q8 | 4 (11.1) | 11 (30.6) | 13 (36.1) | 6 (16.7) | 1 (2.8) | 1 (2.8) | 0 (0.0) |
| Q9 | 5 (13.9) | 11 (30.6) | 13 (36.1) | 6 (16.7) | 1 (2.8) | 0 (0.0) | 0 (0.0) |
| Q10 | 10 (27.8) | 10 (27.8) | 12 (33.3) | 2 (5.6) | 1 (2.8) | 1 (2.8) | 0 (0.0) |
| Q11 | 5 (13.9) | 11 (30.6) | 12 (33.3) | 5 (13.9) | 3 (8.3) | 0 (0.0) | 0 (0.0) |
| Q12 | 13 (36.1) | 13 (36.1) | 7 (19.4) | 1 (2.8) | 2 (5.6) | 0 (0.0) | 0 (0.0) |
Note. A Likert-type scale score of 7.0 represents strong, positive perceptions with the item.
The highest and lowest three items in ranking, by descending order of their means, were the following:
Highest three:
- Did you find the use of colors or other special inking features for coding your notes helpful? (Item 12; M = 5.94, SD = 1.09)
- Did inking on the projected image increase your engagement in the presentation? (Item 3; M = 5.75, SD = 0.87)
- Did you find the use of projected notes with student inking capabilities helpful? (Item 1; M = 5.72, SD = 0.91)
Lowest three:
- Did you learn to have empathy for others’ projected solutions and solution strategies? (Item 8, M = 5.22, SD = 1.12)
- Did you feel that inking in your notes helped you retain and recall information more easily? (Item 7; M = 5.19; SD = 1.06)
- Did you appreciate seeing your comments added to the display? (Item 2; M = 5.17, SD = 1.28)
Table 2
Results of t-Tests with Effect Sizes for the Digital Ink Survey (N = 36)
| Item | Y/N Freq. | M | SD | t-test | Effect Size |
|---|---|---|---|---|---|
| Q1 | 36/0 | 5.72 | 0.91 | 11.31* | 1.89 |
| Q2 | 34/2 | 5.17 | 1.28 | 5.49* | 0.92 |
| Q3 | 35/1 | 5.75 | 0.87 | 12.01* | 2.00 |
| Q4 | 36/0 | 5.61 | 0.93 | 10.35* | 1.73 |
| Q5 | 32/4 | 5.52 | 1.48 | 6.18* | 1.03 |
| Q6 | 35/1 | 5.67 | 1.10 | 9.13* | 1.52 |
| Q7 | 35/1 | 5.19 | 1.06 | 6.73* | 1.12 |
| Q8 | 34/2 | 5.22 | 1.12 | 6.52* | 1.09 |
| Q9 | 36/0 | 5.36 | 1.02 | 8.02* | 1.34 |
| Q10 | 36/0 | 5.64 | 1.20 | 8.20* | 1.37 |
| Q11 | 35/1 | 5.28 | 1.14 | 6.75* | 1.13 |
| Q12 | 35/1 | 5.94 | 1.09 | 10.66* | 1.78 |
* p < 0.001 | |||||
Discussion
The results support the conclusions that preservice elementary teachers who are introduced to effective, high-quality use of digital ink technology for teaching and learning have positive perceptions with the following statements. The statements are in descending order of their means.
- The use of colors or other special inking features for coding notes are helpful.
- Inking on a projected image makes one feel more engaged in the presentation.
- Use of projected notes with student inking capabilities is more helpful than not.
- Use of personalized inked notes is more helpful in preparing for final exams.
- An appreciation exists of the permanency of the inking added to notes.
- The presentation itself becomes a more valuable part of a course.
- Online availability of inkable notes is more convenient than printed notes.
- An awareness of self-knowledge comes though inking in notes.
- Status of beliefs and ideas sometimes change when students hear explanations of other students’ inking.
- More empathy for other’s projected solutions and a solution strategy is learned.
- Inking in notes makes it easier to retain and recall information.
- An appreciation comes from seeing your own personal comments added to the display.
The most interesting finding was not necessarily associated with the survey item with the highest mean, but instead with the survey item for which all participants were in close agreement. The standard deviation shows agreement with an item. Item 3 had the lowest standard deviation of all of the items, meaning that the participants held similar beliefs about the statement that the presentation was an integral part of the course. Further interpretation of these results may suggest that the participants recognized the benefits of learning with this technology and deemed it valuable.
It is also valuable to make note of the survey items with lower means despite the significance and the effect size. Sometimes this effect on the mean can be caused by the response of a few outliers, as demonstrated by the Yes/No frequencies and the frequency of the responses by Likert-type scale values. For example, some students may not have appreciated having their comments added to the display (see Item 2) because they felt belittled when their responses turned out to be associated with unproductive routes or incorrect answers, despite the instructors’ attempt to use them in some way. A classroom culture must be developed by the instructor to help students realize that incorrect answers or unproductive routes are acceptable, helpful, and often necessary in the learning process, especially in mathematics. Students failing to understand this point of conceptual pedagogy may still retain a lower appreciation of their comments being added to the display when they are incorrect.
Additional student comments might be helpful for making interpretations with regard to some of the lower frequencies recorded for the Likert-type item discussing the preference of availability of online inkable notes over printed notes (see Item 5). Several students in the course found that they liked to print the prepared notes before class and interact with the notes in a paper-and-pencil fashion. When approached by the instructor for explanation of this preference students responded in one of two ways, expressing a need to have a hard copy of everything for documentation purposes or not being “good at inking.” Sometimes students have other learning preferences that are higher in status than digital ink technology, and thus, digital ink may not the best medium for learning for all students.
In addition to creating a culture for accepting incorrect answers, an instructor must also help students develop dispositions of empathy and metacognitive thinking. Students might not practice empathy for the projected solutions of others or appreciate a solution strategy if the instructor does not spend time developing this disposition through investigative questions, comments, and challenges. Students will also have difficulty recognizing the benefits of handwritten notes, or in this case, inked notes, on retention or recall of information if the instructor does not direct the students to think metacognitively about their own learning. The development of these two cultural norms in a classroom must be well thought out throughout the course if students are to grasp opportunities to learn these dispositions. The infrequent opportunities for awareness and development of these two dispositions may be the cause of the diminishment of the mean scores (see Items 7 and 8).
Many of the benefits observed by the instructor were similar to the list of statements made earlier in the conclusions. Some additional benefits were noted by the instructors using the digital ink technology that were not measured by the survey instrument. They include the connections that become more clear for the students as the instructor writes on or near the prepared notes with an ad hoc note or illustration; the permanent record that may be kept by an instructor of exactly what expounding was shared during the presentation; the identification and correction that was allowed to take place of students’ naïve conceptions or misconceptions while pre-assessing, the students’ abilities to learn from one another; and the realization of the importance of formative assessment and analysis of student’s written work.
Recommendations and Implications
Studying examples of effective instruction can help define instructional methods that may prove to be successful for other classroom teachers (Schifter, 1996). Instructors and professors should learn to incorporate digital ink technology effectively. Students feel engaged when the prepared notes encourage their direct involvement with the class discussion through inking. When instructors use the types of effective high-quality inking described in the methodology section of this paper, students feel like the inking is an integral part of the lesson rather than just a meaningless incorporation of technology in a course. Instructors should encourage the use of inking as well as color coding and searching notes for items when studying for exams. Last, instructors should consider ways of sharing student solution strategies and creating a classroom culture that makes students more comfortable with learning from each other. Dispositions of empathy and self-knowledge must be taught as one would approach teaching content.
The next steps in this research project and opportunities for future research for other researchers, include examining the types of effective, high-quality inking; clarifying instructional methods for each type; and creating experimental design studies which test their effectiveness in the learning process. In addition, future uses of this technology are on the forefront, and with Microsoft’s Magic Pen even more changes may take place in the near future in ways students and instructors can interact digitally with hard copy documents.
References
Battista, M. T. (2007). Learning with understanding: Principles and processes in the construction of meaning for geometric ideas. In M. E. Strutchens & W. G. Martin (Eds)., The learning of mathematics: National Council of Teachers of Mathematics 69th yearbook (pp. 65-79). Reston, VA: National Council of Teacher of Mathematics.
deLange, J., Burrill, G., Romberg, T. & van Reeuwijk, M. (1993). Learning and testing mathematics in context. Pleasantville, NY: Wings for Learning.
Gravemeijer, K. (1994). Educational development and developmental research in mathematics education. Journal for Research in Mathematics Education, 25(5), 443-471.
Green, S.B., Salkind, N.J., & Akey, T.M. (2000). Using SPSS for windows: Analyzing and understanding data (2nd ed.). Upper Saddle River: Prentice Hall.
Harry Ransom Humanities Research Center. (2005). “Technologies of Writing” examines the history and style of writing. Retrieved July 5, 2007, from http://www.hrc.utexas.edu/news/press/2005/writing.html
Schifter, D. (Ed.). (1996). What’s happening in math class? Envisioning new practices through teacher narratives (Vol. 1. Series on School Reform). New York: Teachers College Press.
Tutty, J., & White, B. (2006). Tablet classroom interactions. In D. Tolhurst & S. Mann (Eds.), Conferences in Research in Practice in Information Technology: Vol. 52. Eighth Australasian Computing Education Conference (pp. 229-233). Hobart, Australia: Australian Computer Society.
Wilson, P.S. (1990). Inconsistent ideas related to definitions and examples. Focus on Learning Problems in Mathematics, 12(3&4), 31-47.
Author’s note:
Kevin Reins
The University of South Dakota
[email protected]
Perceptions of Digital Ink Technology (PDIT) Survey
Circle Y for “Yes” or N for “No” and rate each question’s Y or N response on the continuum (1 to 7) described by the words or phrases given for the endpoints of the scale.
| (1) | Did you find the use of projected notes with student inking capabilities helpful? Y / N | |
| Rate the degree of helpfulness. | 1 2 3 4 5 6 7 | |
| not helpful very helpful | ||
| (2) | Did you appreciate seeing your comments added to the display? Y / N | |
| Rate the degree of appreciation. | 1 2 3 4 5 6 7 | |
| did not appreciate appreciated very much | ||
| (3) | Did inking on the projected image increase your engagement in the presentation? Y / N | |
| Rate the degree of engagement. | 1 2 3 4 5 6 7 | |
| not engaged very engaged | ||
| (4) | Did you perceive the presentation as an integral part of the course? Y / N | |
| Rate the value of the presentation. | 1 2 3 4 5 6 7 | |
| not valuable very valuable | ||
| (5) | Did you feel the online availability of inkable notes more convenient than printed notes? Y / N | |
| Rate the degree of convenience. | 1 2 3 4 5 6 7 | |
| inconvenient very convenient | ||
| (6) | Did you feel using your inked notes were helpful in preparing for the final exam? Y / N | |
| Rate the degree of helpfulness. | 1 2 3 4 5 6 7 | |
| not helpful very helpful | ||
| (7) | Did you feel that inking in your notes helped you retain and recall information more easily? Y / N | |
| Rate the degree of helpfulness. | 1 2 3 4 5 6 7 | |
| not helpful very helpful | ||
| (8) | Did you learn to have empathy for others’ projected solutions and solution strategies? Y / N | |
| Rate the degree of empathy. | 1 2 3 4 5 6 7 | |
| not empathetic very empathetic | ||
| (9) | Did you become aware of your knowledge (e.g., what you did or did not know) through inking? Y / N | |
| Rate the degree of awareness. | 1 2 3 4 5 6 7 | |
| no awareness great awareness | ||
| (10) | Did you appreciate the permanency of the inking you added to the notes? Y / N | |
| Rate the degree of appreciation. | 1 2 3 4 5 6 7 | |
| did not appreciate appreciated very much | ||
| (11) | Did you sometimes change the status of some of your beliefs and ideas when you heard other students’ explanations of their inking? Y / N | |
| Rate the degree of contribution. | 1 2 3 4 5 6 7 | |
| did not contribute contributed a lot | ||
| (12) | Did you find the use of colors or other special inking features for coding your notes helpful? Y / N | |
| Rate the degree of helpfulness. | 1 2 3 4 5 6 7 | |
| not helpful very helpful | ||
Example of Assessing for Instructional Decision-making
Description: The following in-class, inked, pre-assessment demonstrates the instantaneous feedback and gives a glimpse of possible discussions enabled by an AirProjector® and view screen projection system as these tools help the instructor quickly identify misconceptions, known problems, inconsistencies, and naïve conceptions that may be a part of students’ understandings.
Mathematical Task: Move freely between the four sections of the pre-assessment. Class discussion will focus on responses to the pre-assessment items (adapted from Wilson (1990)). The original instrument was administered to sixth- and eighth-grade classes. It is being used here as an example pre-assessment with preservice teachers; similar results were obtained in Wilson’s (1990) study.
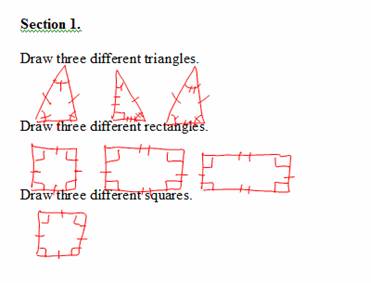
Figure B1. Inked student example of Section 1 of the pre-assessment.

Figure B2. Inked student example of Section 2 of the pre-assessment.

Figure B3. Inked student example of Section 3 of the pre-assessment.
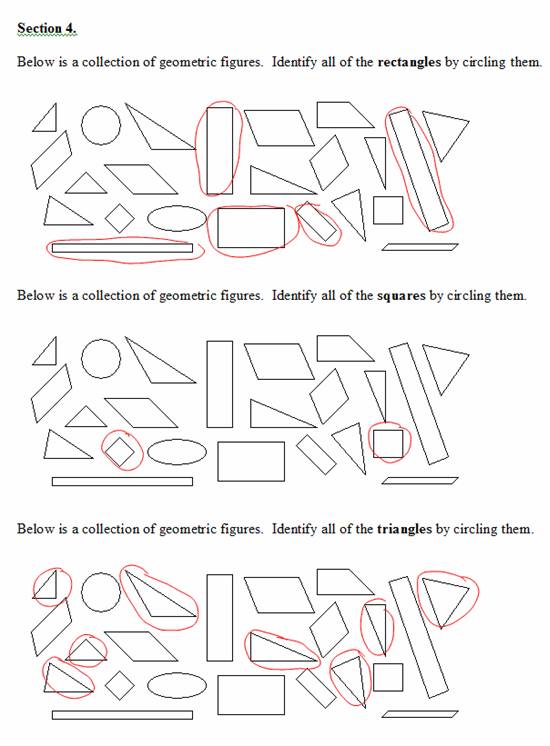
Figure B4. Inked student example of Section 4 of the pre-assessment.
Example of Refining Thinking Processes
Description: The following mathematical task usually produces interior, area-chunking strategies which use whole units and pieces. This strategy most likely results from the first few problems posed by the instructor and tried by students in the downloaded, ink-capable notes. A working algorithm is assembled and refined by building off of incomplete and naïve student ideas that do not work for all cases. The chop-strategy algorithm, which is most clearly defined through a form of recursion, is generated by students through group discussion and analysis of well chosen examples.
Mathematical Task: Develop an algorithm for finding the area of any polygon on a geoboard using prior knowledge and skills of how to find the area of rectangles, right triangles, and other triangles on a geoboard. The polygon, which is a simple closed curve with three or more sides, can be convex or concave. An algorithm is a sequence of instructions that tell how to accomplish a task, like tying your shoes. One example of an algorithm for tying your shoes is the loop, swoop, and pull algorithm, better known as Adam Sandler’s shoe tying algorithm from the movie Big Daddy. But, a good algorithm should be specified exactly, so that (a) there is absolutely no doubt about what to do next, (b) it has a finite number of steps, and (c) it always accomplishes the same goal (e.g., your shoe laces being tied, or in this case, producing the area of any polygon on a geoboard). Type a written explanation of your algorithm and complete the worksheet with nine polygons (see Figure C1) with your invented algorithm. Your algorithm should work for all nine cases on the worksheet.
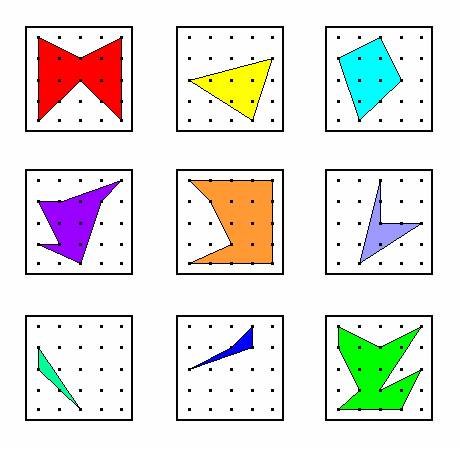
Figure C1. Nine polygons on Geoboards.
If students are getting to the point that they think they have an algorithm that works all of the time, the instructor can project a challenge problem like the concave polygon in Figure C2.

Figure C2. A challenge polygon for developing an area algorithm.
Students will either come up with Figure C3 or parts of C3 to explain their thinking, or it can be displayed using inking as a guide for a student who is very close to verbalizing the idea of recursion in the chop strategy algorithm.
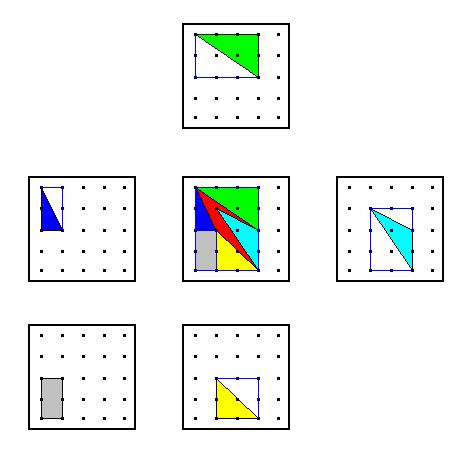
Figure C3. A representation to help explain the recursive chop strategy algorithm.
(Click on image to view animated WMV version.)
The National Council of Teachers of Mathematics (NCTM; 2000) Principles and Standards for School Mathematics ) recommended that students be able to create, test, and choose from among several different algorithms. In order to achieve this expectation an instructor might elicit other invented algorithms discovered during the mathematical task by having individual students project their inked solutions for class review. Another algorithm, which can be developed through the systematization of some simple examples, is Georg Alexander Pick’s formula for finding area. This formula uses B, the number of boundary nails, and I, the number of interior nails, of the polygon region in question. The area is calculated by a formula, A= ½ B + I – 1. One final algorithm that may result from students’ interior chunking algorithms is an Interior Triangles algorithm. Any polygon on a geoboard can be decomposed, on the interior of its region, into triangles. Figure C4 provides a visual representation of the challenge problem given in Figure C2 using this alternative algorithm.
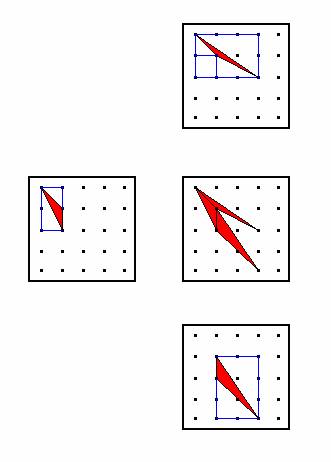
Figure C4. A representation of the Interior Triangles area algorithm.
(Click on image to view animated WMV version.)
Students can be asked which algorithm they liked best and why. Class discussions should center on which algorithm develops the concept of area better for them as learners, is more efficient, is less likely to contain mathematical errors, and is more mathematically elegant.
Throughout this mathematical task, students have been refining their thinking processes by presenting their inked solution strategies, building off of one another’s incomplete and naïve ideas, and making adaptations and changes to their thinking. This entire example was used to accomplish a higher order mathematical problem-solving task, that is, refining strategies until one is found that works in all cases.
Example of Creating Collective Lists of Shared Ideas
Description: The following mathematical task allows students to add the ideas of other students in the class to their lists. Students work on the lists individually first, then in small groups, and then as an entire class. Nonpresenting groups are then able to add new ideas to their lists as other groups present ideas to the class.
Mathematical Task: The instructor places a geometric object on the overhead projector (behind a cardboard screen) and turns on the projector’s lamp. The task is to find (a) objects in your world which could be casting this shadow, and (b) the names of geometric objects, or drawings of geometric objects if you cannot remember their names, which could be casting this shadow.

Figure D1. A collective list of shared ideas from a shadow box activity.
![]()