Graphing calculator technology is recommended by national standards in mathematics (National Council of Teachers of Mathematics, 2000). Even more significantly, research has shown that such technology has a positive effect on student performance (Ruthven, 1990; Smith & Shotsberger, 1997; Tolias, 1993). Reasons teachers employ the technology, however, are varied. Many teachers may not have analyzed why they use graphing calculators or how calculators can help students learn. In NCTM’s Technology Standard (NCTM, 2000), several purposes for graphing calculators and other technology are discussed, including the following:
- Speed: After students have mastered a skill, teachers allow the use of graphing calculators to compute, graph, or create a table of values quickly.
- Leaping Hurdles: Without technology, it was nearly impossible for students who had few skills and little understanding of fractions and integers to study algebra in a meaningful way. Consequently, lower level high school courses often became arithmetic remediation courses. With technology, all students now have the opportunity to study rich mathematics. They can use their calculators to perform the skills that they are unable to do themselves.
- Connections: A sophisticated use of graphing calculators is to help students make connections among different representations of mathematical models. Users can quickly maneuver among tabular, graphical, and algebraic forms.
- Realism: No longer are teachers restricted to using contrived data that lead to integral or other simplistic solutions. Graphing calculators permit the creation of several types of best-fitting regression models. This capability allows data analysis to become integrated within the traditional curriculum; the tedium and difficulty of calculating a best-fit model are no longer factors in introducing data analysis into the curriculum. (pp. 24-32)
Over the years, graphing calculators have become more sophisticated. One relatively recent development is the inclusion of a tutorial on the calculator to help develop skills. The Casio FX2.0 series of graphing calculators features a student tutorial for four different types of algebraic problems: linear equations, linear inequalities, simultaneous equations, and quadratic equations. This tutorial can also be installed on the FX1.0 series. Consequently, a fifth purpose for graphing calculators, facilitating the development of important skills, becomes possible. For this study, we sought to determine if the tutorial helps students learn to solve linear equations.
The linear equation tutorial on the Casio FX2.0 leads students step-by-step through symbolic reasoning to solve a linear algebraic equation. In this study, students used the tutorial to help them solve linear equations during a 3-week unit in a college algebra class. The hypothesis was that this tutorial would increase confidence in doing algebra and enable better understanding of by-hand symbolic manipulation.
Although the degree to which students should be required to master the skills of symbolic manipulation is often a topic of debate among educators, we were convinced both by the literature (e.g., Nathan & Kroedinger, 2000a, 2000b; NCTM, 1989, 1991, 2000; Usiskin, 1995; Waits & Demana, 1992) and the researchers’ experiences that solving linear equations by hand is essential for success in algebra, provides stimuli for higher order mathematics, and helps students understand fundamental algebraic principles that serve as prerequisite skills and concepts for future courses.
Previous Research
Palmiter (1991) studied the use of Computer Algebra Systems (CAS) in a calculus class. Both the experimental and control groups used the same text. However, the experimental group, which used a CAS system, covered the material in 5 weeks; in contrast, the control group took 10 weeks to cover the same material. Furthermore, the experimental group significantly outscored the control group on both computational and conceptual exams; however, despite efforts to ensure the same teaching style, the difference in conceptual scores could be explained by teacher variation. Palmiter also claimed that the experimental group “faired as well” as the traditional group in future classes. Further, the CAS group overall had slightly more confidence in their success in future mathematics courses, and a larger percentage of students in the experimental group indicated that they had learned more in this class than in any other mathematics class. Ninety-five percent of the experimental group claimed they would sign up for another class using a CAS system.
O’Callaghan (1998) studied the effects of a computer intensive algebra (CIA) system on university students in a college algebra course. CIA focused more on concepts, employing symbolic manipulators to perform most of the skills. Three of four hypotheses for greater conceptual understanding were supported, with significant gains found in the ability to model functions, interpret functions, and translate functions. No difference was found in manipulative procedures. Hembree and Dessart (1986) found that, when calculators are integrated with regular instruction, students at all achievement levels show an improved attitude toward mathematics, improved test scores in basic operations, and improved scores in problem solving.
These findings address Bartow’s (1983) fear that students would depend too heavily on the calculator and that their individual skills would “atrophy.” Instead, the use of CAS allows students to generate symbolic, graphical, and numerical representations, to reason with these representations, and to improve students’ work with symbols (Heid, 1997; Heid & Edwards, 2001). These results certainly support the use of technology in the classroom. However, no data have been found regarding a tutorial such as that featured in the Casio FX2.0.
The Tutorial
 |
| Figure 1. Screenshot from the Casio FX2.0 tutorial solving the equation –3x + 5 = –8x – 30 in Automatic mode. |
In addition to a built-in CAS, the Casio FX2.0 has an additional tutorial menu that demonstrates a step-by-step procedure for solving equations. Not only will the Casio FX2.0 solve an equation through the tutorial, but it permits the user to solve the problem without aid in the same step-by-step fashion. It can, in a sense, teach as well as allow practice of symbolic manipulation. Figure 1 shows the screens the tutor shows in solving the equation –3x + 5 = –8x – 30 in Automatic mode. A description of each step appears at the top of the screen, and the results of the particular step are shown below the line. By working through examples such as this, users can then try solving equations on their own, selecting the manual option provided on the calculator.
The central question of this study sought to determine if the Casio FX2.0 tutorial would help students improve their skills in solving linear equations by hand.
Methodology
The study was conducted at a small 2-year liberal arts college with a focus on preparing students for a 4-year college or university. Of the students attending the college, 47% were enrolled in developmental studies and 35% in developmental algebra courses. Ninety-four percent of the students enrolled were traditional students, attending college immediately after high school graduation. Caucasian, African American, and foreign students comprised 44%, 49%, and 7% of the student population, respectively.
The sample was taken from the enrollment in two beginning algebra classes. To control for instructor variability, two sections taught by the same person were chosen. One of these was randomly selected as the experimental group and the other as the control group. Each class had an initial enrollment of 25 students. Information provided by the registrar’s office and a test of SAT scores confirmed that the two classes were roughly equivalent. The instructor also detected no difference between the abilities of the two classes, both of which she perceived as weak. However, she did think that the early start time (8:00 a.m.) for the experimental group caused them to take longer to focus on tasks.
Use of the Casio FX2.0 tutorial was implemented in the experimental class, and students were shown how to use the tutorial early in the semester. The control group used the TI-83 or TI-83 Plus, the calculator required of all students. Although students were allowed to use the Solve feature on the TI-83 or 83 Plus to check their work, use of this feature was not taught. The section on solving linear equations through symbolic manipulation lasted approximately 3 weeks. Students in the experimental group used the tutorial on a daily basis in class as the teacher lectured on step-by-step manipulation. They were also encouraged to use the tutorial while doing homework.
Skill in solving linear equations was measured by a posttest given at the conclusion of the section on solving linear equations. The posttest consisted of 14 linear equations and two word problems that were solved with pencil and paper only; calculators were not permitted (see Appendix A).
Scoring of the problems was based on a rubric provided by the Educational Testing Service Network. Possible scores ranged from 0 to 4, with categories of algebraic knowledge, communication of this knowledge, and demonstration of the skills comprising the score. Scores of 3 or 4 represented successful responses, a 2 represented some conceptual understanding with inconsistent proficiency and incomplete explanations, and scores of 1 or 0 were deemed unsatisfactory. Scoring was done “blindly.”
Two group interviews, one with students in the experimental group and one with students in the control group, were conducted near the conclusion of the unit. Six students in each class, 3 students from the top and bottom quartiles as determined by SAT scores, were randomly selected for the interviews. The questions for both groups included attitudes toward calculators and solving linear equations and general feelings toward mathematics. The experimental group had additional questions concerning the use of the Casio FX 2.0 tutorial. See Appendix B for the interview protocol.
A Likert questionnaire adapted from the Fennema-Sherman scale to inquire about students’ attitudes toward algebra and solving linear equations was administered at the beginning and end of the 3-week study. This scale, originally created in the 1970’s, has been tested and modified several times, and is available in the public domain (see, for example, http://www.woodrow.org/teachers/math/gender/08scale.html). Excerpts from the questionnaire used for this study are provided in Appendix C.
Finally, an anonymous homework questionnaire was administered to the experimental group on five different days during the linear equation unit to determine the extent of use and the degree to which students found the tutorial helpful.
Results
The results of a one-tailed t-test showed that the experimental class significantly outperformed the control class on the posttest (t = 2.09, p = 0.021, df = 47). Overall, mean scores for the two groups were 2.74 and 2.35 out of a maximum of 4, respectively. Posthoc statistics were performed to determine on which questions there was a significant difference between the two groups. The experimental group outperformed the control group on six questions; the control group did not outperform the experimental group on any questions. Interestingly, of the six questions on which the experimental group bested their counterparts, four contained fractions (numbers 2, 4, 8, and 11), with the experimental group average score above 3 on the first three of these. (On Problem 11, the experimental group averaged 1.96, compared with the control group’s 0.52.) On the test, only five problems contained fractions; in fact, the experimental group showed a significant gain on every problem that contained a fraction on both sides of the equation. Further, the experimental group outperformed the control group on multistep problems.
Whether or not these differences occurred for all levels of students in the classes was also investigated. Students were sorted into low, medium, and high groups based on their SAT scores; only students in the medium and high groups had gains on individual questions. The high attrition and failure rate in the lowest performing group might suggest that these students were either unprepared or unwilling to put forth the necessary effort for success.
In addition to the improved performance, there was also a significant increase in attitude from the prequestionnaire to the postquestionnaire for the experimental group (t = 2.11, p = 0.020, df = 47), with the mean attitude increasing from 3.49 to 3.74 on the 5-point scale. There was no significant increase found for the control group (t = 1.35, p = 0.091, df = 47), though their average increased from 3.40 to 3.62. However, upon checking for differences between groups, there was no significant difference between the two groups on either the prequestionnaire or the postquestionnaire (t = 0.81, p = 0.21, df = 44 for the post-questionnaire). Consequently, the results concerning the increase in attitudes are tenuous.
Post hoc analysis showed that gains in attitude occurred for students in the medium group, but not for students in the low or high groups. This result may be due to the low group’s overall poor performance and commitment to their work and to the high group’s overall positive attitudes with which they began the course, leaving little room for gain.
Although the time students in the experimental class spent on homework varied daily, there were some detectable patterns. For the first assignment of the unit, most students spent the majority of their time with the tutorial; all but one student reported it was useful. As the unit progressed, those who perceived the assignments as being difficult spent more time with the tutorial than did those who found the assignments relatively easy. Some students found that the tutorial was difficult to learn, but once learned, it was helpful.
Discussion
The tutorial clearly helped students master the process of solving linear equations. This confirms an important and fifth potential use of graphing calculators in the mathematics classroom, that of developing algebraic skills. Further, the gains appeared on problems that involved fractions and on problems that took multiple steps, areas that often impede students’ progress through upper-level mathematics courses.
The interviews and observations suggest that this additional benefit may have occurred because, to use the tutorial, students had to understand and distinguish coefficients. This understanding apparently transferred to students’ ability to solve linear equations, especially those containing fractions.
In regard to calculator usage, higher-level students took advantage of the calculator, while students in the lower group may have used the calculator as a crutch. One young lady from the lower quartile commented, “It makes it so we don’t have to think.” In contrast, one young man in the upper quartile mentioned, “The tutorial is wonderful!!! It gives us an opportunity to check our answers so we have extra confidence. It is also very useful because it shows us the steps if we forget.”
Although the results concerning improved attitudes are more tentative, students in the experimental group showed a statistically significant improvement in attitudes between the pre-intervention survey and the post-intervention survey, but the control group did not. Further analysis revealed that this difference occurred because of changes in attitudes among students in the middle achievement group; those in the high and low groups did not change attitudes significantly. The ceiling effect may have impeded gains for the high group, and the low group may have been unprepared either academically or motivationally to take advantage of the tutorial. Further research is needed to determine if the immediate availability of “explanations,” the privacy which the tutorial affords, and the endless supply of examples that the tutorial allows contribute to increased confidence, in addition to improved skills, and for which students any benefits are found.
Interviews conducted with students in the experimental class supported the conclusion that the tutorial was beneficial. One student in the medium group summarized his experience as follows: “Before this, I felt scared. I still don’t like algebra, but I feel more comfortable trying to solve these things [equations] because I know I have the answer.”
The gain in understanding of coefficients through work with the tutorial may play a role in helping students in additional, unanticipated areas. During her classes the next semester, the instructor noted that she could identify the students who had been in the experimental class just by their quickness in understanding synthetic division and the factoring process. Interestingly, one student from the experimental group who was doing poorly suddenly blossomed when studying the factoring process. Changes in the performance of other students who had been in the experimental group were also noted. Unfortunately, due to the high attrition rate, the number of returning students was insufficient to conduct any quantitative tests of the results. Nevertheless, this increased ability to use their understanding of coefficients in other areas seems promising and is something that should be explored more fully.
Overall, the evidence suggests that a calculator-based tutorial may have significant benefits for the mathematics classroom. It proved to be an influential learning tool in solving linear equations and perhaps beneficial in improving attitudes. Further, the benefits of strengthening this skill may extend into other unexpected areas.
As supported by the findings here, the tutorial expands the potential benefits of the graphing calculator. In addition to the four purposes stated at the beginning of this article, there is now evidence that the graphing calculator can help accomplish a fifth purpose, that of skill development. Further, though future studies are needed to investigate this more systematically, a sixth purpose seems possible, even likely: that of making connections among different algebraic skills. Although graphing calculators have been used to help students make connections among tabular, graphical, and algebraic representations of functions (e.g., Heid, 1997), the connection among skills is a new, uncharted area. In fact, the tutorial may help in areas that teachers and researchers have not considered or with ideas that teachers may have assumed students already know. While teaching the solution of linear functions, perhaps many teachers emphasize the importance of coefficients and the distinctions between variables and coefficients. In this study, however, it was not until students used the tutorial to solve linear equations that this conceptual connection was recognized and then made.
With forethought, teachers can employ technology to help students learn. Even more exciting, this learning help may extend into areas that are not anticipated. Of course, an inappropriate use of calculators may cause students not to learn what they should, so teachers must always observe and assess their students’ achievement carefully and consistently. Nevertheless, the results of this study demonstrate that there is cause for confidence and even excitement about the benefits that technology can bring to the mathematics classroom.
References
Bartow, D. (1983). Computers and education. Journal of Computers in Mathematics and Science Teaching, 3(1), 8-12.
Heid, M. K. (1997). The technological revolution and the reform of school mathematics. American Journal of Education, 106(1), 5-62.
Heid, M. E., & Edwards, M. T. (2001). Computer algebra systems: Revolutions of retrofit for today’s mathematics classrooms? Theory into Practice, 40(2), 128-137.
Hembree, R., & Dessart, D. (1986). Effects of hand-held calculators in pre-college mathematics education: A meta-analysis. Journal for Research in Mathematics Education, 17, 83-99.
Nathan, M. J., & Kroedinger, K. R. (2000a). An investigation of teachers’ beliefs of students’ algebra development. Cognition and Instruction, 18(2), 209-238.
Nathan, M. J., & Kroedinger, K. R. (2000b). Teachers’ and researchers’ beliefs about the development of algebraic reasoning. Journal for Research in Mathematics Education, 31(2), 168-191.
National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (1991). Professional standards for teaching mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
O’Callaghan, B. (1998). Computer-intensive algebra and students’conceptual knowledge of functions. Journal for Research in Mathematics Education, 29, 21-40.
Palmiter, J. (1991). Effects of computer algebra systems on concept and skill acquisition in calculus. Journal for Research in Mathematics Education, 22, 151-156.
Ruthven, K. (1990). The influence of graphic calculator use on translation from graphic to symbolic forms. Educational Studies in Mathematics, 21, 431-450.
Smith, K. B., & Shotsberger, P. G. (1997). Assessing the use of graphing calculators in college algebra: reflecting on dimensions of teaching and learning. School Science and Mathematics, 97(7), 368-373.
Tolias, G. (1993). The effects of using graphing technology in college precalculus. Dissertation Abstracts International, 50(04), 1274A-1275A.
Usiskin, Z. (1995). Paper and pencil skills in a calculator/computer age. UCSMP Newsletter, 16, 7-14.
Waits, B. K., & Demana, F. (1992). A case against computer symbolic manipulation in school mathematics today. Mathematics Teacher, 85(3), 180-183.
Author Note:
Robert M. Horton
Clemson University
Email: [email protected]
Judy Storm
Andrew College
Email:mailto:[email protected]
William H. Leonard
Clemson University
Email: [email protected]
Appendix A
Post-Test Used to Measure Skills
Solve for x. Work must be shown to receive credit. Calculators are not permitted.
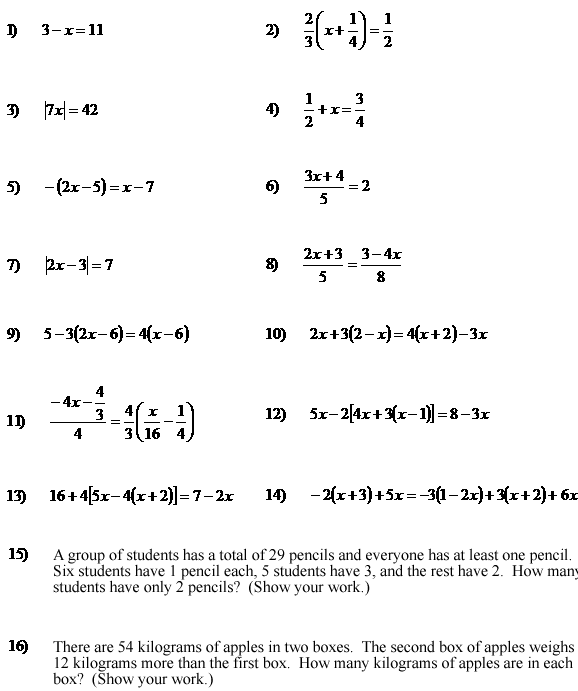
(Note: Room was provided on the test for students to solve the equations.)
Appendix B
Protocol for Student Interviews
Specific interview questions were based on the responses of the students but the following general format was used. Students were expected to explain their responses.
Questions were asked to both groups surrounding their use of technology in the past and interest in Algebra.
- Have you ever used any technology, like graphing calculators, in a math class? If so, when and what technology did you use?
- Would you like (or did you like based on answer above) using this technology in your class?
- Do you like algebra and solving linear equations?
- Do you feel confident solving linear equations?
For students involved in the experimental group, follow up questions were asked if the tutorial seemed helpful.
- Did you use the tutorial to help you solve linear equations?
- Did you like using the tutorial?
- Was the tutorial helpful?
- What is your feeling on using this tutorial for other math classes?
- Think back to before you started the class on solving equations as compared to afterward. Have you changed your opinion? Was the tutorial one of the reasons your opinion changed, if there is a change?
Appendix C
Sample Questions from Attitudinal Survey
Likert Scale Questionnaire
Indicate the extent to which you agree or disagree with each statement. There are no correct answers for these statements.
| 1. | Generally, I have felt secure about attempting to solve linear equations. | ||||
| Strongly Agree A | Agree B | Neither Disagree or Agree C | Disagree D | Strongly Disagree E | |
| 4. | I think I could handle solving more difficult linear equations. | ||||
| Strongly Agree A | Agree B | Neither Disagree or Agree C | Disagree D | Strongly Disagree E | |
| 7. | I’m no good at solving linear equations. | ||||
| Strongly Agree A | Agree B | Neither Disagree or Agree C | Disagree D | Strongly Disagree E | |
| 10. | For some reason, even though I study, solving linear equations seems hard for me. | ||||
| Strongly Agree A | Agree B | Neither Disagree or Agree C | Disagree D | Strongly Disagree E | |
| 26. | I’d be proud to be the outstanding student when it comes to solving learn equations. | ||||
| Strongly Agree A | Agree B | Neither Disagree or Agree C | Disagree D | Strongly Disagree E | |
| 33. | If I had good grades when solving linear equations, I would try to hide it. | ||||
| Strongly Agree A | Agree B | Neither Disagree or Agree C | Disagree D | Strongly Disagree E | |
| Section: __________ | Gender: male or female | ||||
![]()