Overview
In the past 3 years, content-based technology integration has been a significant focus at the University of Colorado at Boulder’s (UCB) School of Education. Assisted by a United States Department of Education’s Preparing Tomorrow’s Teachers to Use Technology (PT3) grant, UCB School of Education faculty and instructors are continually challenged to use technology effectively and innovatively across the teacher preparation program. Using technology appropriately and meaningfully has been an overarching theme across all content areas and, specifically, in mathematics.
Recently, research on cognition and learning has been synthesized in such a way as to focus on four components essential for the development of effective learning environments: community, learner, knowledge, and assessment (National Research Council [NRC], 2000). These four components are fundamental for the successful establishment of any learning environment, whether for student learning or teacher learning and, therefore, form a theoretical framework on which to base an understanding of the necessary characteristics of an effective learning environment.
As diagrammed in Figure 1, the four components of this framework overlap and mutually inform one another. For example, while learner, knowledge, and assessment are embedded within community, these aspects play a large role in forming the community. Each of these components will be defined in the next section of this paper and developed throughout.
The UCB School of Education recognizes this prior cognitive research as a powerful theoretical framework for teaching its preservice and in-service
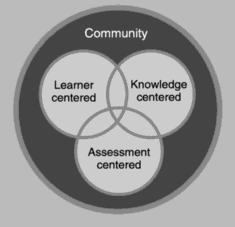
Figure 1. Effective Learning Environment (NRC, 2001, p. 134).
teachers about learning. The authors have collaborated in many ways to improve both mathematics teacher education and technology-integrated education at UCB. We draw from our various works in both domains in order to (a) examine the ways this effective learning environment theoretical framework can be applied to teacher education, (b) focus and apply this effective learning environment framework to the area of technology integration, and (c) tie theory to practice by providing examples of mathematics education technology use in mathematics teacher education that illustrate the effective learning environment framework.
The three technology-supported mathematics education activities presented herein use a Texas Instruments calculator-based laboratory (see http://education.ti.com/us/product/tech/datacollection/features/cbl2.html), The Geometer’s Sketchpad (Key Curriculum Press, 2003), and Fathom Dynamic Statistics Software (Key Curriculum Press, 2002). Community, learner, knowledge, and assessment centered aspects of effective learning environments are discussed in relation to these three examples.
Effective Learning Environments
The editors of How People Learn: Brain, Mind, Experience, and School organized and synthesized volumes of research from areas such as cognitive, social, and developmental psychology and neuroscience to present a framework regarding learning environments that are effective in helping all individuals to learn (NRC, 2000). In their book, they provided “a broad overview of research on learners and learning and on teachers and teaching” that “have a solid research base to support them and strong implications for how we teach” (NRC, 2000, p.14). The four major components of their effective learning environment theoretical framework are summarized in the following sections and later in this paper applied to the areas of mathematics education involving technology and teacher education.
Community-Centered
Community-centered aspects of effective learning environments are important in building a comfortable atmosphere whereby students are encouraged and able to articulate their own ideas, challenge those of others, and negotiate deeper meaning along with other learners (NRC, 2000). In such environments, people are encouraged to learn from one another, to value the search for understanding, and to acknowledge that mistakes are a necessary ingredient if learning is to occur. In such environments, learners are open to new ideas and ways of thinking, as the community members are both encouraged and expected to provide each other with feedback and work to incorporate new ideas into their thinking (NRC, 2000).
When ideas are exchanged and subjected to thoughtful critiques, they are often refined and improved (Borasi, Fonz, Smith, & Rose 1999; Goldman & Moschkovich, 1995). Research indicates that communication is often motivational and helps students to persist in completing tasks and striving for understanding (Cognition and Technology Group at Vanderbilt, 1997; National Council of Teachers of Mathematics [NCTM], 2000).
Learner-Centered
For a century, researchers have been advising that for effective learning to occur education needs to take into account that all people come to know is filtered through their own identities, experiences, and perspectives (Dewey, 1902; Greeno & the Middle School Math Through Application Project Group, 1998). Theodore Sizer (1992) stated,
It is a truism that we learn well only when we are engaged. That is, if we do not pay attention, we will not “get it”. Our attention is caught by things that interest us, that so intrigue us, that we are compelled to find out more about them, that we believe we had better attend to or we might miss something. (p. 85)
Students build new knowledge and understanding on what they already know and believe. Students formulate new knowledge by modifying and refining their current concepts and by adding new concepts to what they already know (Driver, Asoko, Leach, Mortimer, & Scott, 1994). Teachers need to consider and honor this research related to learner-centered aspects of effective learning environments when designing educational activities (NRC, 2000).
Knowledge-Centered
Knowledge-centered aspects of effective teaching environments are important in helping students develop well-organized bodies of knowledge and organize that knowledge so that it supports planning and strategic thinking. In these kinds of environments, students are able to “learn their way around” a discipline (NRC, 2000). Like experts, they are able to make connections among ideas. In these kinds of learning environments, teachers help students think about the general principles or “big ideas” in a subject.
When they learn new knowledge, students should also learn where it applies and how. They should have opportunities to practice using it in novel situations. Students should be able to use what they learn, understand major concepts, build a strong base of supporting factual information, and know how to apply their knowledge effectively (NRC, 2000). They should be able to describe a problem in detail before attempting a solution, determine what relevant information should enter the analysis of a problem, and decide which procedures can be used to generate descriptions and analyses of the problem (Glaser, 1998).
Assessment-Centered
Helping students learn to monitor and regulate their own learning is one of the central tenets of the assessment-centered aspect of effective learning environments (NRC, 2000). Students should question “why it is they believe what they believe, and whether there is sufficient evidence for their beliefs” (White & Frederiksen, 1998, p. 7). This environment provides students with opportunities for feedback and revision. Effective learning requires that students take control of their own learning. Students need to recognize when they understand and when they need more information.
Good learners articulate their own ideas, compare and contrast them with those of others, and provide reasons why they accept one point of view rather than another (NRC, 2000). They are “metacognitive,” that is, they are aware and capable of monitoring and regulating their thoughts and their knowledge (White & Frederiksen, 1998). As Black and Wiliam (1998) noted, it is only when students are trained in and given opportunities for self-assessment that they “can understand the main purposes of their learning and thereby grasp what they need to do to achieve” (p. 74).
Engaging students in assessment of their own thinking and performance allows them to be more self-directive in planning, pursuing, monitoring, and correcting the course of their own learning. “Self-assessment nurtures discovery, teamwork, communication, and conceptual connections” (NRC, 1997, p. 80).
Technology-Supported Mathematics Activities
Technology transforms what is possible in the teaching and learning of mathematics. “The advent of computers and calculators in the classroom facilitates a new approachone where the focus is on reasoning with a variety of representations and understanding the relationships among those representations” (Dugdale et al., 1995, p. 330). Therefore, it is important to provide the next generation of teachers with opportunities to experience firsthand mathematics learning activities that incorporate technology in these ways. These experiences should assist teachers to think critically about the role of technology in teaching and learning (Center for Science, Mathematics, and Engineering Education [CSMEE], 2000). With this goal in mind, preservice teachers taking a mathematics methods course at UCB participated as learners in, and reflected as teachers about, three technology-supported mathematics activities.
Calculator-Based Laboratory Activity
Graphing calculators are commonly available in most schools today (Simmt, 1997). The calculator-based laboratory (CBL) is an extension to the graphing calculator, which can provide learners with a mini laboratory through which they can collect their own data, analyze these data, and give personalized meaning to their mathematics calculations and exercises. The following CBL activity illustrates how technology can be utilized within learning environments to connect mathematical content with an everyday activity in a learner’s lifein this case, that of walking. It was derived from the CBL Systems Experiment Workbook (Texas Instruments, 1994, p. 9).
This activity allows preservice teachers to explore the concept of slope by relating it to the walking motion of a classmate. The activity began by having a preservice teacher in each group walk away from a motion detector that was plugged into a graphing calculator and then having the group interpret the corresponding graph that was formed on the calculator (see Figure 2). Next, the experiment was repeated by having another preservice teacher walk toward the motion detector (see Figure 3).
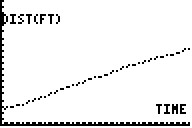
Figure 2. Walking away from CBL.
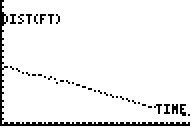
Figure 3. Walking toward the CBL.
The groups were then asked to explain the differences between the graph that was produced from the second experiment (see Figure 3) and that of the first experiment by describing what the x-axis and the y-axis represented. Slope was introduced as the relationship between the change in the distance away from the motion detector (y) and the change in time (x). When the preservice teacher moved away from the motion detector, the distance increased as the time increased to create a graph with a positive slope. When another preservice teacher moved toward the motion detector, the distance decreased as the time increased to produce a graph with a negative slope.
The preservice teachers continued to explore, creating graphs with different slopes by varying their speed. When one individual walked extremely fast, a graph with a steep slope resulted. This logically corresponded with our definition, because their distance changed rapidly while the time increased constantly. When the preservice teachers tried walking slowly, they discovered that the slower they walked the closer they would come to creating a function with a slope of 0; a slope of 0 occurred when there was no change in y. We extended the exploration by challenging the class to create both a positive and negative slope on the graph from one walk.
One individual quickly acted this out by walking away from and toward the motion detector, leading into a discussion on parabolas. The creation of these different graphs, hence, led easily to the formal mathematical definition of slope as the change along the vertical axis divided by the change along the horizontal axis.
The Geometer’s Sketchpad Activity
The Geometers’ Sketchpad (GSP) is a mathematics construction tool developed with teaching and learning in mind. GSP’s dynamic features provide a context from which teachers can expect students to explore, investigate, interpret, represent, and solve mathematical problems as they interact with the software (King & Schattschneider, 1997). The following activity1 was designed to take advantage of GSP’s features and assist
preservice teachers to delve deeply into the concept of differentiation. Derivatives are an area of misunderstanding frequently encountered in beginning calculus classes (Tall, 1991) and, thus, provided the motivation for this activity, based on a standard applied max/min calculus problem:
A farmer has 600 meters of fencing of which to enclose a rectangular pen adjacent to a long existing barn. The farmer will use the barn for one side of the pen and available fencing for the remaining three sides. What is the maximum area that can be enclosed in this way? [This question comes from the calculus textbook by C. Edwards and D. Penney (1998, page 158).]
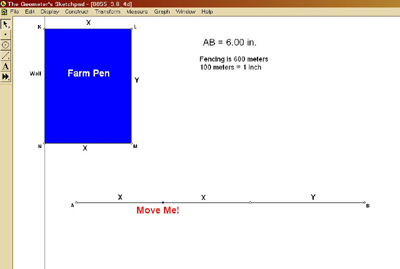
After asking preservice teachers to think about this problem and brainstorm ways to solve it, we discussed the problem. Some wanted to make a table to solve it, others suggested guess and check, and a few thought we could use calculus to solve it, though they were not initially sure how. We suggested that making a model might be helpful and showed them a partly constructed model of the problem that had been preconstructed on GSP (see Figure 4).
Figure 4. Partially constructed model of the GSP farm pen activity.
In the model, the line segment AB represents the constraint of 600 meters of fencing and is divided into two equal pieces, each labeled X and the remaining piece labeled Y to represent the three sides of the pen. The three sides correspond to three sides of rectangle KLMN, which represents the area of the pen to be maximized. After explaining the model, we requested the preservice teachers participating in this activity to note a few things.
First, when the point on segment AB labeled “Move Me!” is moved with the mouse, the two pieces of length X change in unison while still constrained by the total length. Second, the rectangle KLMN correspondingly changes according to the new dimensions X and Y. Thus, the preservice teachers could see how the area of the pen was affected by the change in the way the fencing was partitioned.
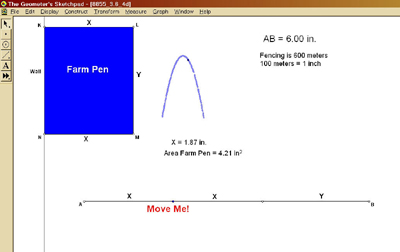
Preservice teachers were then asked to rethink the problem and utilize the model in order to formulate a function of one variable from the situation posed. In this case, we wanted to relate side X with the area of the pen, although either X or Y can be used. With GSP, the preservice teachers were able to explore the graphs of these quantities and observe their relationship. When the point “Move Me!” is moved, the graph shown in Figure 5 is produced.
Figure 5. Derivative relationship expressed in farm pen activity.
This activity visually demonstrates how the area of the pen constructed from a barn, two sides of length X and one side of length Y changes as the lengths of X and Y are manipulated. Because this relationship is nicely illustrated as a parabolic function on GSP, the preservice teachers then recognized that the maximum area is attained when the parabola is at its maximum height or exactly when the parabola has a 0 derivative. “Ah-hah!”the connection between the real-life model and the derivative was understood!
Fathom Dynamic Statistics Activity
Fathom Dynamic Statistics is a data analysis software tool developed with teaching and learning in mind (Finzer, 2000). Like GSP, Fathom’s dynamic features provide a context from which teachers can expect students to explore, investigate, interpret, represent, and solve mathematical problems as they interact with the software. This activity utilizes Fathom’s dynamic simulation abilities in order to facilitate classroom investigation and understanding of the central limit theorem. The main idea of this theorem is that given any distribution of an infinite population with a finite mean and variance, the distribution of the means from repeated samples can be approximated by a normal distribution, the greater the size of the samples the better the approximation. This approximation gets better as the sample size increases and, of course, provides the foundation upon which inferences about the likelihood of obtaining a particular result from one sample can be made.
This activity was originally created and implemented for the third author’s Masters of Mathematics thesis defense. The Fifty Fathoms (Erickson, 2002) activity book contains a recent version of a similar Central Limit Theorem activity.
Preservice teachers’ initial understandings of the central limit theorem were assessed by asking them to look at two survey questions (adopted from Garfield et al., 1999) that showed two different initial distributions. One distribution was “geometric,” which meant that it was skewed right and that values incrementally greater than the mean had a smaller probability of being sampled. One distribution was “uniform,” which meant that every value in the population had an equal probability of being sampled. Preservice teachers were asked to select from several choices and predict what the distribution of 30 samples of size 5 and size 30 from these initial populations would look like. Although individuals had studied the central limit theorem in their statistics classes, they had difficulty predicting a visual representation of repeated samples of varying sizes.
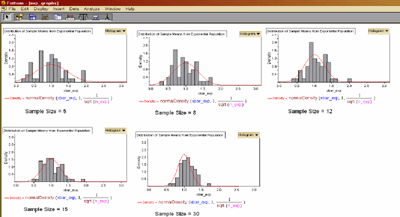
Fathom was then used to run simulations from these different original populations in order to show that the distribution of the sample means taken from these original populations could, in fact, be approximated by a normal distribution. The first data set took samples of varying size from the geometric population. For each sample, the mean was calculated and then the distribution of these sample means was graphed (see Figure 6).
Figure 6. Distribution of sample means from a geometric population modeled in Fathom.
Recall that the original idea was to demonstrate that this distribution is approximated by the normal distribution. As the sample size gets larger, the approximation gets better. In practice, the general rule of thumb is that for samples larger than 30, the normal approximation is good. The normal distribution curve is drawn over the histogram for comparison. Preservice teachers were able to see these repeated samples done in front of their eyes and see how, when the sample size got larger, the distributions of the sample means approached normality.
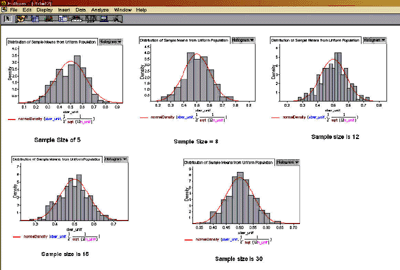
When we asked them to hypothesize what would happen when we simulated drawing from a uniform population, they were able to predict what would happen as the sample size increased. In fact, as the learners compared the distributions of the sample means of a uniform distribution to those from a geometric distribution using the same series of sample sizes, they were able to see and understand another highlight of the Central Limit Theorem, namely, that when starting with a uniform population, the sample means are more quickly approximated (with smaller sample sizes) by the normal distribution (see Figure 7).
Figure 7. Distribution of sample means from a uniform population.
Reflecting on the Technology-Supported Mathematics Activities
Effective learning environments consisting of community, learner, knowledge, and assessment-based aspects are fundamental to a successful learning experience (NRC, 2000). “There needs to be alignment among the four perspectives of learning environments. They all have the potential to overlap and mutually influence one another” (NRC, 2000, p. 154). Each component is necessary within every learning situation. The activities included in this paper provide practical examples of the ways teachers and learners can benefit from attending to the components of effective learning environments. In the next section, we now share theoretical and practical reflections from the authors and the participating preservice teachers, which stem from being involved in the activities described, and demonstrate how each technology-supported mathematics activity exemplified all facets of effective learning environments.
Community-Centered
The learner, knowledge, and assessment-centered aspects of effective learning environments described in this paper are all necessary, yet exist within, and depend upon, the facilitation of a community of learners (see Figure 1). A comfortable and welcoming community becomes the setting in which effective educational activities can be enacted. Without fostering environments that honor learners and the knowledge to be learned, and that invites participation, communication, and collaboration, educational activities are doomed.
Because the community-centered aspect is a unifying construct tying together the other three dimensions of effective learning environments, we provide a synthetic discussion of how this community-centered construct flows through the other dimensions and can set the context for the successful implementation of technology-supported mathematics activities.
All of the activities were cultivated within a community of learners setting. “Community-centered perspectives of effective learning environments involve the degree to which they promote a sense of community” (NRC, 2000, p. 154). All of the participating preservice teachers’ beliefs and understandings regarding content and pedagogy were honored, encouraged, and respected.
The authors who facilitated these activities and the preservice teachers who participated in them share a commitment to understanding the intricacies of mathematics teaching and learning. When these aspiring teachers are able to share their ideas about mathematics and education, the thinking of the whole community is furthered. This level of comfort and openness contributed to and was enhanced by learner, knowledge, and assessment centered components of these technology-supported activities.
Learner-Centered
One goal of these technology-supported mathematics activities was to help preservice teachers enjoy learning and make connections between the content in these tasks and their prior knowledge. The calculator-based technology, for example, created an energetic social atmosphere whereupon the preservice teachers could make a connection with slope by physically walking a positive or negative slope. They were quickly engrossed in understanding the concept of slope and modeling slopes of varying degrees. By connecting the routine everyday event of walking with a mathematical representation of this phenomenon, these learners were able to see how mathematics, science, and technology relate to, and can help them understand, their world. Furthermore, they gained the experience and opportunity upon which they can continue linking their physical surroundings with the symbols and numbers of science.
Both the GSP and Fathom activities took advantage of the dynamic, visual nature of technology and helped class members build deeper conceptual understandings of topics they had studied before but not fully understood. These activities supported learners in building on their prior procedural experiences with derivatives and the Central Limit Theorem, respectively, and involved them in aligning their existing knowledge with visual conceptions of these concepts.
Participating teachers were engaged throughout these activities in a supportive and engaging learning environment in which they were able to think about, discuss, and build on their prior understandings. Alternative examples to formal symbolic representations, such as these simulations, are important because preservice teachers have diverse ways of learning and making connections. Building from prior experiences, learning styles, and understandings is an integral part of learner-centered practices.
The preservice teachers found these three activities easy to understand as learners and believed they would be productive and useful in their own teaching. When asked to reflect on these activities, one preservice teacher stated,
A student becomes more submerged into a topic when given a task or activity to complete that is related to ideas presented . They’re engaged, wondering about what they’ve witnessed. So they are more likely to actively learn the content, rather than passively.
This is exactly the point of the learner-centered tenets of effective learning environments and nicely illustrates what is required in an effective learning environment. Mathematics education principles and standards aim to support students in developing robust understandings and to build the empowerment and ability for students to be able to participate critically in an ever-increasing technological society (Center for Science, Mathematics, and Engineering Education, 2000; Keitel, 1989; NCTM, 2000). These grand educational goals can be realized only when students are motivated, engaged, and supported in moving in this direction.
Knowledge-Centered
All of the technology-supported activities described were developed with clear content learning goals in mind. This clear content focus is key to honoring knowledge-centered aspects of effective learning environments. Using technology for technology’s sake is not sufficient, nor conducive, to cultivating content understanding. Teachers must clearly identify concepts that students have difficulty understanding and develop activities that will support student investigation of that content. Knowledge-centered tenets of effective learning environments assist students to go beyond procedural and rote memorization and to build deep conceptual understandings (NRC, 2000).
The concepts of slope, derivative, and sampling distributions can all be approached in a purely symbolic manner, or in a way that bridges procedural and conceptual perspectives in order to develop deep understandings. These technology-supported mathematics activities aimed to support teachers in participating as students and reflecting as educators on tasks that take the latter approach.
The GSP activity required the teachers to explain and articulate derivative characteristics and consequences within a different situation than one that directly asks them to find the first derivative of an equation, set the equation equal to 0, and solve. Participants in the CBL activity necessarily had to conceptualize and articulate how changes in speed and distance resulted in changes in slope. The Fathom activity asked teachers to investigate the Central Limit Theorem with different initial population distributions and sample sizes from these distributions in order to understand and apply this theorem.
When asked to reflect on these tasks, one preservice teacher appropriately noted, “Many students have a hard time understanding what the formulas for these concepts mean and why they work.” Another preservice teacher commented,
By having students participate in these kinds of activities, I think it will have a lasting impression for the students and they won’t just try to remember the formulas because that is what they are supposed to do, but because they understand the process.
These reflections summarize some of the important goals of the knowledge-centered component of effective learning environmentstasks should allow students the opportunity to “learn their way around” the discipline and make connections and form robust understandings.
Assessment-Centered
Technological simulations can be used to illustrate assessment-centered features of effective learning environments. They can provide a medium through which students can repeatedly make conjectures, test applications, and evaluate their results. Each of the technology-supported mathematics activities described was facilitated in such a way that teachers were given the time and the expectation to think about the results before they finished the simulations. The conjecture and reflection phases are essential. By questioning what results they believe will occur when they enact simulations and by continuing to run simulations while positing different outcomes, preservice teachers are metacognitively developing their understandings.
Prior to running the Fathom simulation, for example, it was important that the preservice teachers were asked to make predictions to describe the distributions of the sample means for simulations of varying sizes. Answering questions like the following necessitated thinking about what they would see happen before the simulation was run: “Will the distribution of sample means from a sample of size n from this population look more like the original population or more like a normal distribution?” (adopted from Garfield et al., 1999).
Through this ongoing cycle of conjecture, application, and evaluation, these teachers were able to develop a more robust conceptual understanding of the often difficult to understand Central Limit Theorem (Derry, Levin, Osana, Jones, & Peterson, 2000; Lajoie, 1998). Similarly, teachers had to think about what type of graph they would see on their calculator if they moved in a certain direction from the CBL and how they could maximize the area of the farm pen before they examined the GSP simulation.
The kinds of opportunities for classroom investigation and discourse afforded by each of the technology-supported activities described in this paper are essential for students to be metacognitive about their own understandings and see “how it all fits together” (NRC, 2000). The preservice teachers unanimously indicated that the simulations were a critical component for deepening their understandings of these concepts and that they want their students to have similar opportunities to participate in and think about these kinds of activities.
Conclusions
In the examples described in this paper, the mathematics teacher education program at UCB provided opportunities for preservice teachers to themselves learn in and reflect upon facilitating effective learning environments. Often, preservice teachers are not comfortable revealing that they do not understand some mathematics content. Here, they participated within a safe, supportive community of learners and were able to do so. These types of experiences allow teachers to develop understandings regarding mathematics content and pedagogy and to feel what it is like to be among a community of learners.
While participating in these CBL, GSP, and Fathom activities, these preservice teachers were asked to align their procedural and conceptual understandings of mathematics and encouraged to share their reasoning regarding their understandings, both as learners and as aspiring teachers. They were encouraged to share their developing understandings of mathematics and teaching with the instructors and with fellow students.
For example, when participating in the activities related to the concepts of derivative and the Central Limit Theorem, these aspiring teachers were able to make connections, have those illuminating “ah-hah” moments, and simply, yet very importantly, be excited about their learning. These experiences, we hope, will transfer to their own teaching. “Perhaps the central goal of all the teacher preparation and professional development programs is in helping teachers understand the mathematics they teach, how their students learn that mathematics, and how to facilitate that learning” (NRC, 2001, p. 398).
Because these preservice teachers were able to participate in collaborative learning, communicate with one another and the instructors, and share their beliefs and understandings openly, they can now envision their own classrooms taking this shape. Developing a true community of learners is an essential and overarching feature of effective learning environments (NRC, 2000).
The teacher education program at UCB immerses preservice teachers in an environment that supports them in becoming critical, confident, and able reform-based practitioners (Borko et al., 2000). Tomorrow’s teachers have shown that they value the opportunities for increased motivation, connection, and understanding that are provided by effective learning environments. The conversations of these preservice teachers support how technology-supported investigative activities, such as those described here, help to develop these environments.
By having their own opportunities to observe, practice, and reflect on these kinds of educational activities, these aspiring teachers have discovered for themselves that technology can help facilitate effective learning environments that are community, learner, knowledge, and assessment centered. These preservice teachers have experienced and reflected upon how these components are interconnected and come together to support effective learning environments.
One may ask if these teachers are truly ready to use technology-supported mathematics activities with their students successfully. Although utilizing these kinds of tasks as novice teachers with students who have a wide range of content understandings and learning styles will likely be challenging, these aspiring teachers are ready to try. The first step is often the hardest; beliefs are the hardest factor to influence and the main barrier to changing teachers’ practices (Putnam & Borko, 2000).
By having participated in and reflected upon this pedagogy, these teachers now have a vision of what effective learning environments can look and feel like and are poised to try and enact these kinds of successful teaching and learning situations with their own students.
Hovermill (2003) highlighted that when technology is integrated into mathematics education practice in such a way that all components of the theoretical framework are met, profound learning environments do indeed result. Undoubtedly, teacher learning is a continual process (CSMEE, 2000; NRC, 2001) and these novice teachers will benefit from continued support reflecting on implementing these practices. However, the experiences described throughout this paper provide these beginning teachers with a model that can guide their way.
In this paper we (a) critically examined the ways that this theoretical framework regarding effective learning environments can be applied to teacher education, (b) focused and applied this learning environment framework to the area of technology integration, and (c) tied theory to practice by providing examples of mathematics education technology use in mathematics teacher education that illustrated the effective learning environment framework.
Situating the previously described technology-supported activities within this theoretical framework highlights how technology can provide the opportunities to see this theory put into practice in exciting, innovative, and effective ways.
NCTM (2000) stated that by “using technological tools, students can reason about more general issues and they can model and solve complex problems that were heretofore inaccessible to them” (p. 26). The next generation of teachers must be provided opportunities to experience reform-based instruction as learners and to practice facilitating this pedagogy themselves. It is our hope that this work of situating practical technology-supported activities within a powerful theoretical framework on learning will continue to be shared and will be useful to others.
Technology, in and of itself, is complex. Yet even more complicated is finding ways in which to use it as a tool for teaching and learning. Guided by this theoretical framework, technology supported activities can work meaningfully in a learning environment that research proves effective.
References
Black, P., & Wiliam, D. (1998). Assessment and classroom learning. Assessment and Education, 5(4), 7-75.
Borko, H., Peressini, D., Romagnano, L, Knuth, E., Yorker, C., Wooley, C., Hovermill, J., & Masarik, K. (2000). Teacher education does matter: A situative perspective of learning to teach secondary mathematics. Educational Psychologist, 35(3), 193-206.
Borasi, R., Fonz, J., Smith, C., & Rose, B. (1999). Beginning the process of rethinking mathematics instruction: A professional development program. Journal of Mathematics Teacher Education, 2(1), 49-78.
Center for Science, Mathematics, and Engineering Education. (2000). Educating teachers of science, mathematics, and technology: New practices for the new millennium. Committee on Science and Mathematics Teacher Preparation. Washington DC: National Academy Press.
Cognition and Technology Group at Vanderbilt. (1997). The Jasper project: Lessons in curriculum, instruction, assessment, and professional development. Hillsdale, NJ: Erlbaum.
Derry, S., Levin, J., Osana, H., Jones, M., & Peterson, M. (2000). Fostering students’ statistical and scientific thinking: lessons learned from an innovative college course. American Educational Research Journal, 37(3), 747-773.
Dewey, J. (1902). The child and the curriculum. Chicago: University of Chicago Press.
Driver, R., Asoko, H., Leach, J., Mortimer, E., & Scott, P. (1994). Constructing scientific knowledge in the classroom. Educational Researcher, 23(7), 5-12.
Dugdale, S., Thompson, P., Harvey, W., Demana, F., Waits, B., Kieran, C., McConnell, J., & Christmas, P. (1995). Technology and algebra curriculum reform: Current issues, potential directions, and research questions. Journal of Computers in Mathematics and Science Teaching, 14(3), 325-337.
Edwards, C., & Penney, D. (1998). Calculus. New York: Prentice Hall
Erickson, T. (2002). Fifty fathoms. Oakland, CA: Eeps Media.
Finzer, W. (2000). Design of Fathom, a dynamic statistics environment, for the teaching of mathematics. Paper presented at the International Conference on Mathematics Education. Copenhagen, Denmark.
Garfield, J., delMas, R., & Chance, B. (1999). The role of assessment in research on teaching and learning statistics. Paper presented at the annual meeting of the American Educational Research Assocation, Montreal, Canada. Retrieved December 23, 2003, from http://www.gen.umn.edu/research/stat_tools/aera1999/assessment.htm
Glaser, R. (1998). Education for All: Access for learning and achieving usable knowledge. Prospects, 38(1), 7-20.
Goldman, S., & Moschkovich, J. (1995, October). Environments for collaborating mathematically. In J. Schnase & E. Cunniues (Eds.), Proceedings of the First International Conference of Computer Support for Collaborative Learning (pp. 143-146). Bloomington, IN.
Greeno, J.G. and the Middle School Math Through Application Project Group (1998). Theory and practices of thinking and learning to think. American Journal of Education, 106, 85-126.
Hovermill, J. (2003). Technology-supported inquiry learning with Fathom: A professional development project. Unpublished doctoral dissertation. University of Colorado-Boulder.
Keitel, C. (Ed.) (1989). Mathematics, education, and society. Paris: UNESCO
Key Curriculum Press. (2002). Fathom dynamic statistics [Computer software]. Retrieved December 23, 2003, from www.keypress.com/fathom
Key Curriculum Press. (2003). The geometer’s sketchpad [Computer software]. Retrieved December 23, 2003, from www.keypress.com/sketchpad
King, J., & Schattschneider, D. (1997). Geometry turned on!: Dynamic software in learning, teaching, and research. Washington, DC: The Mathematical Association of America.
Lajoie, S. P. (Ed.). (1998). Reflections on statistics: Learning, teaching, and assessment in grades K-12. Mahwah, NJ: Erlbaum.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
National Research Council. (1997). Inquiry and the National Science Education Standards: A guide for teaching and learning. Washington, DC: National Academy Press.
National Research Council. (2000). How people learn: Brain, mind, experience, and school. Washington, DC: National Academy Press.
National Research Council. (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press.
Putnam, R., & Borko, H. (2000). What do new views of knowledge and thinking have to say about research on teacher learning? Educational Researcher, 29(1), 4-15.
Simmt, E. (1997). Graphing calculators in high school mathematics. Journal of Computers in Mathematics and Science Education, 16(2), 269-289.
Sizer, T. (1992). Horace’s school: Redesigning the American high school. Boston, MA: Houghton Mifflin Company.
Tall, D.A. (Ed.). (1991). Advanced mathematical thinking. Netherlands: Kluwer Academic Publishing.
Texas Instruments Incorporated. (1994). CBL system – Experiment workbook. Retrieved December 23, 2003, from http://education.ti.com/us/product/tech/cbl/down/cblwb.html
White, B., & Frederikson, J. (1998). Inquiry, modeling, and metacognition: Making science accessible to all students. Cognition and Instruction, 16(1), 3-118.
Acknowledgements
The work reported in this paper was supported by the Department of Education Preparing Tomorrow’s Teachers to Use Technology (PT3) Grant, Award Number P342A000115.
Endnotes
1This activity, inspired by Pat Thompson (personal communication, 2000) can be accessed at (http://education.colorado.edu/faculty/
peressini/farmpen.htm). For construction steps and The Geometers’ Sketchpad files for this activity, contact [email protected].
Contact Information:
Jeffrey Hovermill Shamatha
Department of Mathematics and Statistics
Northern Arizona University
Flagstaff, AZ
email: [email protected]
![]()