When Stuart asked, “Can you technically do 2Πr for … any polygon?” referring to finding perimeter, Beth was caught off guard. To recover, she tried to balance her own mathematical understanding with an attempt to understand Stuart’s question. She also moved back and forth between attempting to find both flaws and merits in his thinking.
The data used to narrate this story of Stuart’s conjecture were collected for a previous study. For that study we answered the following research question: How does a teacher (professor) play the believing game (Elbow, 1986) in a college mathematics class? We moved beyond revealing that a professor played the game (Harkness, 2009) to illuminating when and under what circumstances the believing game practice occurred (Harkness & Noblitt, 2017).
Elbow (1986, 2006) contended that educators can improve their practice of understanding by the processes of methodological belief and methodological doubt. Both of these processes are systematic, disciplined, and conscious efforts. Believing transpires when teachers endeavor to find virtues and strengths, no matter how unlikely students’ answers or conjectures might seem. Doubting occurs when teachers attempt to find flaws or contradictions in students’ answers or conjectures.
According to Elbow (1986, 2006), one process should not dominate an educator’s practice at the detriment of the other. However, anecdotally, we contend that doubting by mathematics teachers, finding flaws or contradictions, overshadows believing in most classrooms. Interestingly, Elbow’s framework has been embraced and practiced in literacy education with writing. How would the use of these processes by mathematics teachers play out in classrooms?
We explored this question in previous research and specified the paradoxes inherent in their use. For example, imagine the following scenario: A teacher hears a student answer or conjecture she deems to be incorrect: “To divide fractions I can divide the numerators and divide the denominators.” In order to utilize methodological doubt the teacher believes in her own assumptions and mathematical understanding. This statement is indeed false if the only method she knows is the so-called “keep it – flip it – change it” approach or the multiplication-by-the-reciprocal memorized procedure. End of conversation.
In order to utilize methodological belief, however, she doubts her own assumptions and mathematical understanding and attempts to tease out what the student has described, the student’s mathematical understanding, and what is right about the conjecture. In fact, the teacher may even come to the realization that the student’s conjecture was correct. The classroom conversation is dramatically different when the teacher believes (Elbow, 1986; Harkness & Noblitt, 2017).
In the actual classroom conversation captured with video and described within this paper, the teacher, Beth (second author), moved back and forth along a continuum between the two processes of methodological belief and methodological doubt and two other processes, which we named “reserved believing” and “reserved doubting.” Rather than wholeheartedly embracing believing and doubting when she heard Stuart’s conjecture, reserved believing occurred when she moved along a continuum toward believing and attempted to find strengths or merits. Reserved doubting occurred when she moved along a continuum toward doubting and attempted to find weaknesses or flaws in his conjecture.
In fact, together we were able to identify this back-and-forth progression because we had captured the episode in the moment (Wiliam, 2007) via video. Rewatching the video multiple times allowed us to identify an opportunity missed in the moment to reflect upon Stuart’s conjecture and then to mathematically explore Stuart’s conjecture about the relationship between perimeter and circumference after the moment of teaching (Harkness, 2014).
We also noticed how Stuart attempted to establish his own sense of internal authority (Schoenfeld, 1992; Wilson & Lloyd, 2000) with his mathematical conjecture. This internal authority is, indeed, rare but critical for students who have “little idea, much less confidence, that they can serve as arbiters of mathematical correctness, either individually or collectively” (Schoenfeld, 1992, p. 62). Therefore, the purpose of this narrative is to describe the believing and doubting that occurred and to highlight the missed teaching opportunities in the moment which provided future opportunities for our own learning after the moment.
Literature
Reflective Thought and Believing and Doubting
More than a decade ago, Dewey (1910) in his seminal work, How We Think, described reflective thought as a problem-solving chain of thoughts that compels inquisitiveness with purpose. Indeed, according to Dewey, reflective thinking involves basing conclusions “upon evidence” (p. 6). He delineated two subprocesses used in every reflective operation: “(a) a state of perplexity, hesitation, doubt; and (b) an act of search or investigation directed toward bringing to light further facts which serve to corroborate or to nullify the suggested belief” (p. 3).
For teachers today video might be used to find evidence. However, rather than using doubt (Dewey) as the default mode of thought to draw conclusions about a student’s answer or conjecture, a teacher might refrain from judging the conjecture or answer as wrong but attempt to first use belief (Elbow, 1986; 2006). According to Elbow (1986), “This [believing] may be our only hope of seeing something faint that is actually there which she [the student] is particularly good at seeing but the rest of us are ill suited to see” (p. 259).
To summarize, reflective thought is a problem-solving process based on evidence that begins with perplexity or doubt (Dewey, 1910), yet this problem-solving process might begin with perplexity or belief. Additionally, teachers can attempt to believe either during a lesson or after a lesson with the use of video recorded in the moment of teaching.
The Use of Video to Capture in-the-Moment Teaching
The use of video to capture in-the-moment teaching has many powerful implications. Video allows teachers to watch and rewatch fast-paced and relentless classroom interactions and then reflect upon and engage in conversations with others about what transpired during mathematics lessons. Video permits teachers to notice when their teaching efforts were focused elsewhere or reflect on things that may have been done differently (Star & Strickland, 2008).
When teachers watch video of themselves interacting in their own classrooms, video can help them confront their visionary images of teaching and their beliefs about teaching and learning with their actual teaching practice (Donnay & Charlier, 1990).
Video provides a space for teachers to become aware of the tensions between their purported beliefs and the teaching pedagogy they see in the video. Accordingly, reform can ensue when “teaching becomes learning for the teacher,” which is possible with the use of self-capture video (Sherin & Han, 2004, p. 181).
In recent years, the use of video to help teachers notice has gained increased emphasis in teacher education. According to van Es and Sherin (2002), noticing has three components:
(a) identifying what is important or noteworthy about a classroom situation; (b) making connections between the specifics of classroom interactions and the broader principles of teaching and learning they represent; and, (c) using what one knows about the context to reason about classroom events. (p. 573)
Studies have reported positive results when video is used for purposes of noticing (Rosaen, Lundeberg, Cooper, Fritzen, & Terpstra, 2008; Santagata & Guarino, 2011; Seidel, Stürmer, Blomberg, Kobarg, & Schwindt, 2011; Sherin & Han, 2004; Star & Strickland, 2008; Tripp & Rich, 2012; van Es, Stokero, Sherin, Van Zoest, & Dyer, 2015).
Sherin and Han (2004) recruited a group of four mathematics middle school teachers to participate in their study of video club. The teachers watched video from two participating teachers’ classrooms during the course of the academic year, 1996-1997. Teachers moved from talking about themselves or the other teachers in the videos to talking about the students in the videos. Furthermore, the discussions of student thinking moved from simply restating student ideas to analyses of student thinking. These transformed conversations were facilitated by the researchers when they asked about students’ statements and ideas.
Sherin and Han (2004) reported that prior to their study other researchers had shown that without facilitation teachers tended to watch video with a focus on the teacher and classroom management issues (Hammer, 2000; Richardson & Kile, 1999), and teachers who listened to, endeavored to make sense of students’ ideas, and learned from those ideas had the most success in effecting reform in their classrooms (Franke, Carpenter, Levi, & Fennema, 2001). For those reasons Sherin and Han chose to facilitate those kinds of conversations during video club meetings.
Participants in the study conducted by Seidel et al. (2011) were German science teachers. Researchers wanted to find out the impact of teachers viewing videos of their own teaching or videos of other teachers teaching. Teachers’ analysis of their own videos resulted in “more activating experiences” compared to teachers’ analysis of other teachers’ teaching videos. However, Seidel et al. cautioned that watching their own videos could trigger self-defense mechanisms and, according to Eraut (2000) they may then automatically use “deceptive discourse” to analyze and discuss their practice in order to mask actions that might lead to criticisms of their teaching practice.
Another study with classroom teachers was realized by Tripp and Rich (2012). Their research focused on how video of seven teacher participants’ own classrooms and teaching impacted their reflective practices and, ultimately, changed their teaching practices. The teachers recorded classroom lessons for 2 months and reported that self-reflection with the use of video was more beneficial than when they were merely recalling what happened in the moment of teaching. According to Tripp and Rich, “Teachers reported that video encouraged change because it helped them (a) focus on key aspects of their teaching, (b) gain a new perspective, (c) trust the feedback they received, (d) feel accountable to change their practice, (e) remember to implement changes, (f) see their progress” (p. 737).
Three elementary preservice teachers participated in the Rosaen et al. (2008) study of noticing. Researchers were interested in the effects of video compared to “from memory” reflections. They found that video-supported written reflections by the preservice teachers in their teaching internships were more specific, more focused on instruction rather than classroom management, and more devoted to the children in their classrooms rather than to the preservice teachers’ themselves. Technology “allows moments to be frozen in time” (p. 358) through focus on specific clips of teaching episodes.
Preservice teachers (n = 27) also participated in the study directed by Santagata and Guarino (2011). They asked the preservice teachers to view two types of videos, of classroom teachers and of interviews with children. The preservice teachers then responded to prompts which asked them to describe the lessons or interviews and “… things that you thought were interesting in terms of student learning of the content and teaching strategies. You may watch the video multiple times [italics in the original]” (p. 140). They coded the written responses for “productive reflections.” Santagata and Guarino recommended “highly scaffolding” preservice teachers’ viewing and analysis experiences, coupling the use of video with live observations, and addressing the “distance”’ that preservice teachers may feel between their own teaching and the teaching they observed in the videos.
In another study with preservice teacher participants, Star and Strickland (2008) used three video assessments. For the preassessment the preservice teachers watched a video in class and answered a questionnaire about the video. They then viewed a second video, this time outside of class, and wrote about it. Finally, for the postassessment, the preservice teachers watched a third video in class and completed the same preassessment questionnaire. Additionally, they observed an actual classroom teacher and wrote a paper in which they were to describe “… with as much richness and depth as possible, all that happened in the one class period” (p. 115).
Findings suggested that preservice teachers did not begin methods coursework with proficient observation skills. However, the course they took and the course assignments led to significant increases in their observations related to noticing aspects of the classroom environment, the mathematics of the lesson, and discourse between the teacher and students. Researchers recommended that improving the skills of noticing should be an explicit aspect of initial coursework and assignments in tertiary mathematics methods classes.
Using previous research findings, van Es et al. (2015) proposed recommendations for ways mathematics teacher educators should facilitate the use of “self-captured” video recorded by preservice and in-service teachers. Their suggestions included the following: make the purpose of the video activity explicit from the start; provide multiple opportunities for self-capture video; and, support teachers in creating and implementing lessons/tasks that are rich in mathematics and discourse.
“We propose that the act of deliberately participating in the self-capture process as well as viewing and analyzing one’s own video with colleagues, offers worthwhile opportunities for mathematics teacher learning” (van Es et al., 2015, p. 6). Again, this notion of teacher learning emerged as an important reason for the use of video. Van Es et al. underscored the significance of recording lessons rich in mathematics and mathematical discourse.
Without those components, teachers’ reflections might focus merely on what occurred at a surface level or on classroom management issues. With those components, teachers’ reflections might focus on the students’ mathematical understanding, the teacher’s mathematical understanding, and the ways future lessons may be developed or improved based on the observations made by watching the video. The story narrated within this paper highlights Stuart’s conjecture and the professor’s in-class reaction, as well as the professor’s reflection after watching video of the classroom conversation.
Methodology
For the original study (Harkness & Noblitt, 2017), the particular context was Beth’s classroom, her students, and Shelly (first author). Beth was not consciously attempting either believing or doubting while the data were collected. However, we were attempting to answer the research question: How does a teacher (professor) play the believing game (Elbow 1986) in a college mathematics class?
Instead of trying to merely describe Beth’s practice when she unconsciously believed or doubted, as we would do with interpretive research, we discussed understandings or explanations of her practice of believing and doubting teacher actions with a hermeneutic approach (Kimball & Garrison, 1999), which assumes that understanding is a productive process that occurs within a particular context, among particular participants. The purpose of hermeneutical inquiry “is to raise questions rather than to answer them, to ask about rather than to conclude for, and to make a place where positions can occur rather than speak from positions” (Silverman, 1994, p. 31). The narrative study described in this paper resulted from other questions that emerged when we watched video and had opportunities to listen to Stuart’s voice multiple times, reflect on what transpired, and play with the mathematics.
The Course Setting and Context
Beth was one of four mathematics educators in a mathematics department of a midsize metropolitan university in the midwestern United States, and she regularly taught the two courses observed for this study. The three-credit required courses were designed specifically for students studying to become elementary teachers or middle grades mathematics teachers; about one fourth of them were preparing to become middle grades mathematics teachers. Typically, students in these courses were in their second or third year of college.
The content of the first course included problem solving, number sense and numeration, number systems, number theory, and patterns and functions. The content of the second course included problem solving, algebra, and geometry. They were held during consecutive 8-week sessions within a 16-week semester. The overall goal of both courses was to introduce the students to mathematical concepts important to the understandings of elementary mathematics and to develop the art of problem solving.
Students in both courses were expected to explain, justify, and apply mathematical concepts. Class meetings occurred Mondays, Wednesdays, and Fridays, 1:00-2:50 pm. During about one third of the time students worked in small groups, and the other two thirds of the time was devoted to lecture. Students used the following manipulatives throughout the semester: pattern blocks, base 10 pieces, base 5 pieces, colored counters, three-dimensional solids, Polydrons™, dot paper, tracing paper, compasses, straightedges, and protractors.
Data Collection and Analysis
The phases of research for the original study were iterative and inductive (as in Creswell, 2012). Shelly took field notes and videotaped 36 class sessions; she transcribed 12 class sessions verbatim in order to get a deeper understanding of the classroom conversations. These 12 were chosen because as Shelly took field notes she thought Beth was, possibly, believing during these particular class sessions. As Shelly transcribed the video she used the field notes to help analyze the data, coding for a priori categories of believing or doubting.
It was not the intent of this research to analyze the data for how many times the a priori categories occurred or for what percent of the time Beth seemed to believe or doubt. As per our research question, we wanted to describe how Beth believed and to find episodes that showed the classroom interactions when she believed.
Next, we identified more nuanced episodes when Beth seemed to be doubting what she perceived to be wrong answers and believing what she perceived to be wrong answers, and we came to consensus about the episodes that portrayed these categories. These categories helped explain and understand, at a broad conceptual level, Beth’s actions and the interactions between her and the students. In order to increase complexity, we also considered context (Flick, 1998) and used the transcripts of the interviews to help triangulate the data.
During the final interview we watched video when the segments of believing and doubting occurred to facilitate simulated recall. It was during this process that we generated the categories of reserved believing and reserved doubting.
Additionally, Shelly facilitated five audio-recorded conversations with Beth; four occurred throughout the semester while videotape data were collected, and one occurred a year later. During these conversations we focused on the students, the mathematics, and Beth’s practices. Our goals with each conversation were twofold: to answer the original research question and to raise new questions. During the final conversation we watched segments of video in which Beth seemed to either believe or doubt. It was during this conversation that we initially contemplated Stuart’s conjecture and his thinking. Within this paper we “restory” (Creswell, 2012) chronologically what transpired in the moment in the classroom, our later conversations, and our after-the-moment mathematical explorations of Stuart’s conjecture.
These methods resulted in attainment of verisimilitude or plausibility and transferability rather than “truth,” as Polit (2010) noted:
The researcher’s job is to provide detailed descriptions that allow readers to make inferences about extrapolating the findings to other settings. The main work of transferability, however, is done by readers and consumers of research [emphasis added]. Their job is to evaluate the extent to which the findings apply to new situations. It is the readers and users of research who “transfer” the results. (p. 1453)
In essence, transferability happens when our restorying provides opportunities for shared meanings while reading the text and opportunities for reflection at the end of the text (Ellis, 1998). Furthermore, according to Connelly and Clandinin (1994), teacher education is a process of learning to tell and retell educational stories. Sustained conversations in which we listen to responses to these stories allows for “added possibility” in using them to “encourage more mindful retellings” (Connelly & Clandinin, p. 150). Let the story begin.
The Lesson
The goal of this lesson was to use a regular polygon to derive the formula for the area of a circle. Specifically, Beth first led the students through finding a formula for the area of a regular hexagon. Her plan was then to use that formula, along with the idea that as n gets bigger the area of a regular n-gon approximates the area of a circle, in order to determine the formula for the area of a circle. In order to meet this goal, Beth drew a regular hexagon with side length s and apothem r, with a triangle formed by the center of the hexagon and two adjacent vertices (see Figure 1).
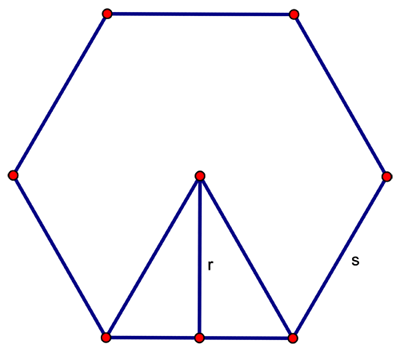
Because there are six such congruent triangles within the hexagon, Beth talked about how to use the area of one of those triangles to find the area of the hexagon. Thus, the area of this regular hexagon is 6(½sr) = 6s(½r). At this point, she noted that 6s is the perimeter of the hexagon and that generalizing this information, ns is the perimeter of a regular n-gon. Subsequently, along with the fact that as n gets bigger a regular n-gon approximates a circle, it is true that as n gets bigger the perimeter approximates the circumference of a circle. At this point in a typical class, Beth would be ready for the punchline: “Thus, the area of the circle is 2Πr(½r) = Πr2.” This approach was her plan for the lesson. Stuart had other ideas. Stuart had questions about the n-gon “becoming” a circle. The video allowed us to notice how Beth seemed to move back and forth between reserved doubting and doubting Stuart’s conjecture. The following conversation transpired (S is Stuart and T is Beth):
S: … At what point is, does it [n] get big enough that where you can…
T: It doesn’t really matter because I could always make it bigger. It, here’s the point where it gets big enough: infinity. How about that? You see what I’m saying? [Reserved doubting]
No response.
T: So like, so like if I said “a thousand,” and you said, “Well, no, I don’t think that’s, I don’t think that’s big enough.” I could say, “Okay, make it a thousand and one.” You said, “It’s still not big enough.” I said, “Okay, make it two thousand.” “Still not big enough.” “Okay.” You see what I’m saying.
No response.
T: So I don’t know. [Reserved doubting]
S: Could you technically do 2Πr for, like, any polygon? Like, the way I’m thinking of it is sort of like a TV, like, the triangles would be, like, the most basic pixel, you know what I mean? As you continue on the spectrum, you know, the circle becomes like a super high-resolution, super small pixel. So could you, like, essentially, like, you know, treat these polygons as …low resolution circles. …
T: Yes.
S: So could you use 2Πr for any polygon?
T: Not really. [Doubting] So it doesn’t work perfectly because… Here are two reasons that I can think of. One, I don’t know what the radius is, and that’s what r is. And two, this relationship holds for circles, but what does that mean for a polygon? What does that mean… for a triangle? Circumference, I guess you could say the measurement around. Okay. Fine. But the diameter? [Draws an equilateral triangle on the board] Like, what does that even mean? [Doubting]
S: I mean … wouldn’t it be the center of the triangle because … Wouldn’t it all be the same because if you draw the center [T puts a point in the approximate “center” of the equilateral triangle], like that far, if you use one of the angles [vertices]. Okay, and just draw a line through it. That’s going to be the same length as if you drew any line [not necessarily through a vertex] as long as it passes through that central point. That length is going to be the same throughout, because you may be losing ground on, on one. You’d be losing ground on one portion but gaining it on the other portion.
T: Uh, I don’t think that is. … So if that’s the center [refers to the drawing of the equilateral triangle], I don’t think that length is the same as that length [this is what S said above when he referred to “losing ground” and “gaining ground”].
S: Okay. That makes sense.
T: You see what I’m saying?
S: Yeah.
T: So I don’t know what to call the diameter. …You could maybe make something up and say, “Well, I’m only going to call the diameter when you go through a vertex.” I don’t know. You’re inventing something there, and it may work. [Reserved believing] But we don’t have it right now. You know what I’m saying? But I love what you’re doing, because you’re trying to make, you’re trying to make these connections. (Class transcript from video, April 17, 2013)
Stuart asked a higher order thinking question. He turned Beth’s question around on her. She asked, “How can you use the formula for the area of a regular polygon to find the formula for the area of a circle?” Stuart responded, “Can you use the formula for the area of a circle to determine the area of a regular polygon?” This was a question that she had honestly never thought about. Also, by using the analogy of pixels, Stuart gave her something else to think about: How are pixels related to the limit ideas present in this classroom discussion?
Beth ended the class meeting with a comment that implied Stuart was asking good questions and attempting to make mathematical connections. It ended there, however. There was no real follow up on his comments or his conjectures.
Reflection with the Use of Video
Beth did not think much more about this classroom episode until she and Shelly met to watch it and reflect on what had happened. We were watching the video in order to identify episodes in the class where Beth was believing and doubting.
After watching the video and referencing the transcript, we focused on different parts of the classroom exchange. First, recall Stuart’s comments below when Beth asked him what the diameter of a triangle would be.
I mean … wouldn’t it be the center of the triangle because … Wouldn’t it all be the same because if you draw the center, like that far, if you use one of the angles [vertices]. Okay and just draw a line through it, that’s going to be the same length as if you drew any line as long as it passes through that central point. That length is going to be the same throughout because you may be losing ground on, on one. You’d be losing ground on one portion but gaining it on the other portion. (Class transcript from video, April 17, 2013)
After watching the video, Beth said,
Okay, if it’s regular maybe we could do something with that, but then I have to think about the polygons that aren’t regular, and that’s going to be a mess, so,…no…. So if it’s regular…. Yeah, so okay, if it’s regular what’s the diameter…. What does he say? He says the center of the triangle. Well, what’s the center of the triangle? Well, there are lots of different centers of the triangle actually. So, what center are we talking about? And they don’t know that. So we’d have to get into what we mean by the center of the triangle. Or maybe we wouldn’t, but I’m just trying to think of maybe what I was thinking at this point. Maybe we could get around that, but that could be…well what does center even mean? It goes through a vertex and the center. We could call that the diameter. Okay. And then pi, because I think I heard myself say that this relationship holds for circles. So do I use pi? You know, so once I find that length….I mean this could all be a conversation that I’m having with them. (Interview, April 4, 2014)
This was a real learning moment for Beth. As she was thinking further about Stuart’s comments, Beth realized she could have prompted him with questions that might have given her more understanding of his mathematical thinking and understanding. These same questions and the discussion that arose could have also furthered her own mathematical understanding. Continuing the discussion with Stuart might have ended with possible answers to the questions, “When can you use 2Πr to find perimeter?” and “How can we adapt our understanding of radius and diameter to expand when we can use 2Πr to find perimeter?” Unfortunately, Beth chose to end the conversation with Stuart.
Shelly noticed something about how this classroom scenario differed from other classroom scenarios in which Beth engaged in believing. During the interview in which she and Beth watched the classroom video with Stuart, Shelly noticed,
Perhaps with the other segments we watched [where believing was observed], you followed up with a question instead of…. Here, you didn’t really follow up with a question to get at more of his thinking. Does that make sense? Whereas, I feel like with the other ones you were saying, “Well, tell me more,” “‘Let’s draw this out,” or “What do you mean by the center?” (Interview, April 4, 2014)
It was true. In this particular scenario, Beth was either doubting or using reserved doubting. She believed that her mathematical viewpoint was the only correct viewpoint to have, and she was trying to find flaws in Stuart’s thinking. Unfortunately, it was not until after the classroom episode had occurred and we were watching the video that we decided to explore the mathematics of Stuart’s conjecture. While it is regrettable that it was after the fact and the students could not be a part of the exploration, it still speaks to the power of video as a tool for noticing and reflecting. Watching the scenario play out again prompted us to engage in mathematical investigation.
Making Sense of Stuart’s Conjecture
Our curiosity about Stuart’s conjecture and attempt to believe rather than doubt, prompted us to play around with shapes and look for connections between circumference and perimeter. We sat at a table in Beth’s office and Shelly drew polygons on graph paper (see Figures 2 and 3) while Beth used Geometer’s Sketchpad™ for her exploration.

The process that Shelly first used was to find the center of the equilateral triangle with sides of length 24 and a perimeter of 72. Next, she drew line segments (to simulate possible radii of the triangle). Using the Pythagorean Theorem to calculate the lengths of each of the 12 radii, she listed those lengths and then found the average length, which was about 10.157. Finally, assuming the radii of this triangle to be 10.157 and using the formula for circumference, the approximate perimeter of the triangle would be 66.413, which is 5.587 less than the actual perimeter. Close, but would using a square (see Figure 3) instead of a triangle give a more accurate approximation?

Using a slightly different process, Shelly first drew a square with sides of length 24 and a perimeter of 96. Taking the average between the shortest radii from the center of the square and the longest radii from the center of the square (again using the Pythagorean Theorem), she found the average radii to be approximately 14.485. Using this radii and the formula for the circumference she found an approximate perimeter of the square to be about 91. The difference between the approximate perimeter and the actual perimeter was about 5, which was a closer approximation. Would the difference continue to decrease if she used a regular pentagon, a regular hexagon, etc.?
Beth used Geometer’s Sketchpad™ (GSP) to explore Stuart’s question. At first, she used a similar approach as Shelly, but on Sketchpad. She wanted to consider lots of different radii of the triangle. Figure 4 shows her sketch.

Using Sketchpad, Beth calculated the actual perimeter of this triangle to be 23.47 cm. To explore Stuart’s thinking, she used 2Πr to approximate the perimeter of the triangle. She defined a radius as a segment connecting the circumcenter of the triangle (E) to a point (F) on a side of the triangle (in this figure, side AC). By dragging point F alongside AC of the triangle, Beth determined the range of perimeter approximations for this approach to be 16.39 cm to 21.29 cm, yielding a mean perimeter approximation of ½(16.39 + 21.29) = 18.84 cm. The actual perimeter was not even in the range of approximations. This begged the following questions: What if we considered a square instead of a triangle? Would the range of approximations be smaller? Would the actual perimeter be within the range of approximations? Beth investigated these questions. Figure 5 is a screenshot of the GSP exploration.

Using the same definition of radius and the previous approach, Beth determined the range of perimeter approximations to be 23.19 cm to 32.80 cm, yielding a mean perimeter approximation of ½(23.19 + 32.80) = 27.995 cm. This came as a surprise. The range of perimeter approximations was greater with the square than the triangle. Beth had expected the range of perimeter approximations to be smaller for the square. This time, however, the actual perimeter was within the range. Beth continued her investigation with a regular hexagon (Figure 6).

The range of perimeter approximations using BC as the radius was 23.18 cm to 26.74 cm, with the actual perimeter being within that range at 25.56 cm. The mean perimeter approximation was ½(23.18 + 26.74) = 24.96. Also, the range of perimeter approximations using the hexagon was smaller than the range of perimeter approximations using the square, and both of those ranges included the actual perimeter. Thus, the technique of using the segment determined by what we called the circumcenter and a point on one side of the polygon was more accurate for the hexagon than the square. This discovery made intuitive sense, considering the notion that as n gets bigger, a regular n-gon approximates a circle.
During these explorations, Beth was struck with the notion that there may be other ways to define the radius of a polygon. She decided to explore some of these alternative definitions using a triangle as the polygon. Figure 7 is a screenshot of the sketch that has three different conceptualizations of the radius of triangle ABC.

With each different definition of radius, Beth used 2Πr to determine the perimeter of the regular triangle. First, she defined the radius as half of the length of a segment through a vertex perpendicular to the opposite side (Line Segment CB). With this length as the radius of the triangle, the perimeter is 25.59 cm. Next, she considered the length of Line Segment DA, the segment connecting a vertex to the circumcenter of the triangle, as the radius. With this length as the radius, the perimeter of the triangle is 34.12 cm.
Finally, she considered the radius of the triangle to be the perpendicular distance from the circumcenter of the triangle to a side of the triangle (Line Segment AB). This definition of radius gave a perimeter of the triangle to be 17.06 cm. The actual perimeter of the triangle is 28.22 cm. Are different definitions of radius more strategic? Why or why not? What happens when n gets bigger? These questions could prompt yet another interesting turn in the investigation of different definitions of radius and the connection to 2Πr.
Implications
This study featured one teacher (professor), one classroom, and one classroom episode – delimitations in some sense – but we wanted to capture more the essence, or heart, of what transpired when we attempted to believe Stuart’s conjecture. The results of this study are not generalizable but transferable (Politt, 2010).
Technology, video, and Geometer’s Sketchpad, advantaged us to rewatch the episode multiple times and then play with the mathematics suggested by Stuart’s conjecture. Is it possible to attempt to believe after the professor and the students have left the classroom? This is not a question that Elbow (1986, 2006) or others researching and writing about believing and doubting have asked. Based on our own exploration, we assert that video has the potential to be a powerful tool for mathematics teacher educators to use with preservice teachers or in professional development settings to explore teacher actions of believing and doubting. In fact, we have used video of Stuart’s conjecture and other video-recorded episodes from Beth’s classroom in mathematics methods courses for preservice teachers and in conference presentations to demonstrate teaching episodes where Beth employed believing, doubting, reserved believing, and, reserved doubting teacher actions (Harkness & Noblitt, 2017).
After showing the episodes, we posed questions about both pedagogy and content. Anecdotally, the preservice teachers and classroom teachers seemed intrigued by the differences between Beth’s actions during each episode and asked thoughtful questions regarding both pedagogy and mathematics.
Finally, the use of video after the moment allowed us to consider ways to incorporate Stuart’s conjecture into future lessons. Van Es et al. (2015) suggested teachers’ reflections might focus on how future lessons may be developed or improved based on observations made when watching self-capture video. Indeed, Beth created a worksheet for students in a subsequent mathematics course she taught, and students explored the historical connections between Stuart’s conjecture and Archimedes’ system of finding the perimeters of inscribed regular polygons and circumscribed regular polygons to approximate pi (http://betterexplained.com/articles/prehistoric-calculus-discovering-pi/; Harkness & Noblitt, 2017). Therefore, the use of video can have implications for teachers’ future lessons.
Conclusion
By watching the video, we made observations about doubting, reserved doubting, and reserved believing teacher actions that Beth used when she heard Stuart’s conjecture. Beth was unclear in the moment about how to make sense of Stuart’s conjecture related to pixels and how to use his thinking to expand the use of 2Πr to find the perimeter of a polygon. She attempted to find flaws in his thinking. However, through the power of video as a tool for noticing and reflecting, she moved towards reserved believing and then believing after the moment.
Video permitted us to capture in-the-moment teaching and then use it to reflect on teaching, learning, and the mathematics. Teaching became learning for the teacher (Sherin & Han, 2004) and the researcher. Video for noticing and reflecting also allowed us to delve deeper into the mathematics as described in this paper. Although Rosaen et al. (2008) noted that technology “allows moments to be frozen in time” (p. 358), when Stuart made his conjecture the video actually allowed us to unfreeze both the pedagogy and the mathematics.
While it may be unfortunate that Stuart and the other students in his class did not directly benefit from this after the moment believing, we were able to explore mathematics because of the thinking that Stuart’s original classroom conjecture prompted. Video can, perhaps, allow teacher educators to help preservice teachers and classroom teachers notice and reflect on missed opportunities for believing. Video also has the potential to empower teachers to explore the mathematics suggested by students after the moment and then use what they learn in future lessons.
References
Connelly, F. M., & Clandinin, D. J. (1994, Winter). Telling teaching stories. Teacher Education Quarterly, 145-158.
Creswell, J. W. (2012). Educational research: Planning conducting, and evaluating quantitative and qualitative research (4th ed.). Boston, MA: Pearson Education.
Dewey, J. (1910). How we think. Boston, MA: D.C. Heath & Co.
Donnay, J., & Charlier, E. (1990). Understanding education situations: Training educators for the analysis of practice. Brussels, NE: De Boeck.
Ellis, J. L. (1998). Teaching from understanding: Teacher as interpretive inquirer. New York, NY: Garland Publishing.
Elbow, P. (1986). Embracing contraries. New York, NY: Oxford University Press.
Elbow, P. (2006). The believing game and how to make conflicting opinions more fruitful. In C. Weber (Ed.), Bringing light into the darkness: A guide to teaching peace, empathy, and understanding (pp. 16-25). Portsmouth, NH: Heinemann.
Eraut, M. (2000). Non-formal learning and tacit knowledge in professional work. British Journal of Educational Psychology, 70(1), 113-136.
Flick, U. (1998). An introduction to qualitative research. London, UK: Sage Publications Ltd.
Franke, M. L., Carpenter, T. P., Levi, L., & Fennema, E. (2001). Capturing teachers’ generative change: A follow-up study of professional development in mathematics. American Educational Research Journal, 38(3), 653-689.
Hammer, D. (2000). Teacher inquiry. In J. Minstrell, & E. van Zee (Eds.), Inquiry into inquiry learning and teaching in science (pp. 184-215). Washington, DC: American Association for the Advancement of Science.
Harkness, S. S. (2009). Social constructivism and the ‘Believing Game’: A mathematics teacher’s practice and its implications. Educational Studies in Mathematics, 70(3), 243-258.
Harkness, S. S. (2014). Recycling plastics: Utilizing ‘moments of contingency’ for formative assessment. Louisiana Association of Teachers of Mathematics, 10, 13-26.
Harkness, S. S., & Noblitt, B. (2017). Playing the believing game: Enhancing productive discourse and mathematical understanding. Journal of Mathematical Behavior, 45, 63-77.
Harkness, S.S., & Noblitt, B. (2017). Pixels: Creating lessons with historical connections between perimeter and circumference. Ohio Journal of School Mathematics, 76, 22-30.
Kimball, S. L., & Garrison, J. (1999). Hermeneutic listening in multicultural conversations. In V. R. Fu & A. J. Stremmel (Eds.), Affirming diversity through democratic conversations (pp. 15-27). Upper Saddle River, NJ: Merrill.
Polit, D. F. (2010). Generalization in quantitative and qualitative research: Myths and strategies. International Journal of Nursing Studies, 47, 1451-1458.
Richardson, V., & Kile, R. S. (1999). Learning from videocases. In M. A. Lundberg, B. B. Levin, & H. L. Harrington (Eds.), Who learned what from cases and how? The research base for teaching and learning with cases (pp. 121-136). Hillsdale, NJ: Erlbaum.
Rosaen, C. L., Lundeberg, M., Cooper, M., Fritzen, A., & Terpstra, M. (2008). Noticing noticing: How does investigation of video records change how teachers reflect on their experiences? Journal of Teacher Education, 9(4), 347-360.
Santagata, R., & Guarino, J. (2011). Using video to teach future teachers to learn from teaching. ZDM Mathematics Education, 43, 133-145.
Schoenfeld, A. H. (1992). Reflections on doing and teaching mathematics. In A. H. Schoenfeld (Ed.), Mathematical thinking and problem solving (pp. 53-70). Hillsdale, NJ: Erlbaum.
Seidel, T., Stürmer, K., Blomberg, G., Kobarg, M., & Schwindt, K. (2011). Teacher learning from analysis of videotaped classroom situations: Does it make a difference whether teachers observe their own teaching or that of others? Teaching and Teacher Education, 27, 259-267.
Sherin, M. G., & Han, S. Y. (2004). Teacher learning in the context of a video club. Teaching and Teacher Education, 20, 163-183.
Silverman, H. J. (1994). Textualities: Between hermeneutics and deconstruction. New York, NY: Routledge.
Star, J. R., & Strickland, S. K. (2008). Learning to observe: Using video to improve preservice mathematics teachers’ ability to notice. Journal of Mathematics Teacher Education, 11, 107-125.
Tripp, T. R., & Rich, P. J. (2012). The influence of video analysis on the process of teacher change. Teaching and Teacher Education 28, 728-739.
van Es, E. A., & Sherin, M. G. (2002). Learning to notice: Scaffolding new teachers’ interpretations of classroom interactions. Journal of Technology and Teacher Education, 10(4), 571-596.
van Es, E. A., Stokero, S. L., Sherin, M. G., Van Zoest, L. R., & Dyer, E. (2015). Making the most of teacher self-capture video. Mathematics Teacher Educator, 4(1), 6-19.
Wiliam, D. (2007). Keeping learning on track: Classroom assessment and the regulation of learning. In F.K. Lester, Second handbook of teaching and learning mathematics (pp.1053-1098). Charlotte, NC: Information Age Publishers.
Wilson, M. R., & Lloyd, G. M. (2000). The challenge to share mathematical authority with students: High school teachers’ experiences reforming classroom roles and activities through curriculum implementation. Journal of Curriculum and Supervision, 15(2), 146-169.
![]()