Emphasis on mathematical practices in mathematics education is growing in policy and research. Fueled, in part, by the inclusion of both processes and proficiencies in both Common Core State Standards (CCSS, 2010) and the Next Generation Science Standards (NGSS Lead States, 2013), teachers are expected to support the development of practices—behaviors that support investigation, model building, and learning in science and mathematics—in their students and, in particular, argumentation and coming to certainty.
Arguing is central to reasoning, especially mathematical reasoning (Mercier & Sperber, 2011; Oaksford, Chater, & Hahn, 2008); yet, mathematical reasoning and argumentation skills are neither innately endowed nor acquired early or easily (Hahn & Oaksford, 2012; Kuhn, 1991; Oaksford et al., 2008). Promoting the development of mathematical argumentation in middle and high school students has become a focus of attention in research and curriculum.
In this paper, we describe our recent work focused on supporting students’ development of argumentation through small group collaboration using a multi-user dynamic geometry software (DGS) environment. Specifically, we explored how argumentation might develop in an online environment that allows small groups to synchronously create, manipulate, conjecture, and discuss dynamic geometry sketches. The foci for the current study involved exploring the individual and collective development of argumentation through understanding both the structure of student interaction in online collaborative DGS sessions and the ways that structure evolved over time.
This work serves as an existence proof for the potential of online, multi-user DGS in supporting students as they participate in and ultimately develop productive argumentative practices. We explored this issue via a case study of three eighth-grade participants in a supplemental geometry program using an online, distributed DGS. The result is particularly important, given that many current teachers are not adequately prepared to enact instruction focused on higher order practices (Working Group on the Common Core State Standards, 2011).
Background
The current research is situated within the successful Virtual Math Teams (VMT) Project, an National Science Foundation funded project that developed a virtual learning environment that enabled mathematical collaboration at a distance. The original VMT software included a variety of features, including a shared whiteboard, synchronous text chat, and a referencing tool that allows users to connect visually specific portions of the whiteboard with relevant chat postings. In addition to supporting student mathematical collaboration, student actions and postings are logged and can be replayed for use in teacher professional development or for fine-grained analysis of the interactions.
Previous VMT research used a qualitative micro-analytic approach to study small group mathematical problem solving in the VMT environment. Previous analyses have documented successful unfacilitated student problem solving at a distance and the differences between online chat-based conversation and in-person interaction (Stahl, 2009). Additionally, Stahl argued that students working together were able to solve problems that individual students, working alone, could not.
More recently, the VMT project has incorporated GeoGebra v.4.3.32.0—an open-source DGS that lets users create dynamic mathematics objects and explore content from geometry, algebra, and beginning calculus—into the VMT system. The new version of the VMT software, VMT with GeoGebra (VMTwG), enhances the VMT environment to include all the features of GeoGebra, including dynamically linked algebra, graphical, and numerical (spreadsheet) mathematical representations.
The VMT Project Team thus produced the first multi-user instance of GeoGebra that allows users to create, collaborate, manipulate, and discuss GeoGebra sketches while, at a distance, maintaining the legacy features of the VMT (multiple tabbed whiteboard pages, synchronous chat, and the ability to connect chat and whiteboard through referencing). Figure 1 shows a screenshot of a typical VMTwG session. Each of the tabs across the top are separate GeoGebra panes that have all the standard GeoGebra functionality and can either be blank or prepopulated with sketches by an instructor. The window also displays a list of all the users currently in the VMT room, and a historical record of the chat session. Additionally, in order to avoid simultaneous actions within VMTwG, users take control of the GeoGebra functionality using the button at the bottom of the window.
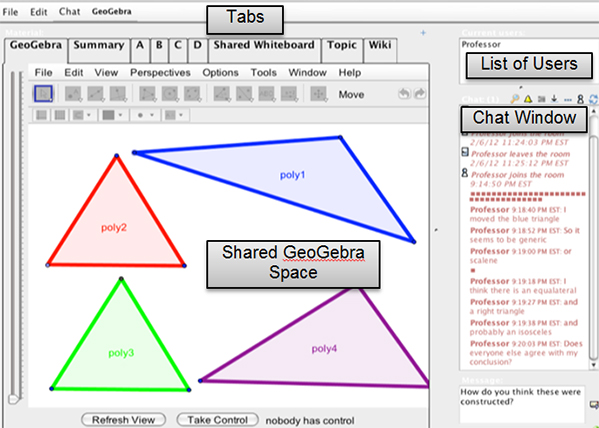 Figure 1 . A typical VMTwG Window (including multiple tabs, a GeoGebra pane, a list of active users, and the chat history).
Figure 1 . A typical VMTwG Window (including multiple tabs, a GeoGebra pane, a list of active users, and the chat history).
Figure 2 illustrates the referencing feature, which allows users to connect explicitly a chat post with either a previous chat post or a specific portion of a GeoGebra window. In Figure 2, for example, the user is able to clearly indicate the point discussed in the post (Point D, which is on the circle and also on the segment).
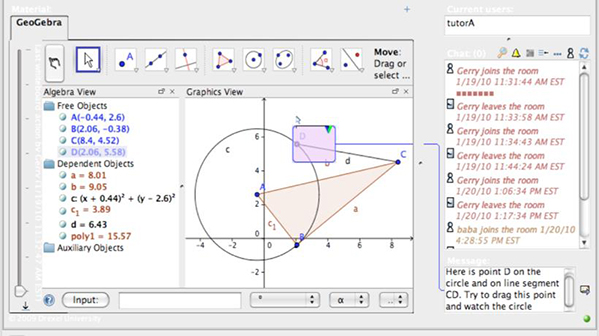 Figure 2. Referencing in VMTwG.
Figure 2. Referencing in VMTwG.
Building on previous research that documented the impact of DGS on student achievement and problem solving (Christou, Mousilides, Pittalis, & Pitta-Pantazi, 2005; Isiksal & Askar, 2005; Reimer & Moyer, 2005) , the project team conjectured that the inclusion of DGS into VMT and the ability to generate and explore mathematical relationships, constructions, and dependencies would enhance students’ mathematical activity within VMT.
Theoretical Orientation
Broadly, the current research is grounded in the emergent perspective (Cobb & Bauersfeld, 1995; Cobb & Yackel, 1996), which highlights the reflexive relationship between individual cognitive development and the social interactions in which individuals participate (Cobb, 2000). From this perspective, documenting learning involves coordinating analysis of collective mathematical activity, primarily through a focus on the emergence of social and sociomathematical norms and collective mathematical practices (Cobb, Stephan, McClain, & Gravemeijer, 2001; McClain & Cobb, 2001), and analysis of individual activity and cognition.
While the emergent perspective provides the theoretical connection between participation in social activities (e.g., discourse and interaction) and individual development, the presence and use of technology (including computers, the Internet, and software for collaboration) may fundamentally change the way knowledge is produced (Borba & Villarreal, 2005). As such, we build on Borba and Villarreal’s theoretical notion of humans-with-media or, more broadly, humans-with-technology, which highlights that “knowledge is always constructed by collectives that involves humans and different technologies” (p. 170) and emphasizes the fact that different combinations of participants, facilitation, and technology are likely to support different kinds of collective activity and knowledge construction.
Much like the paper and pencil and chalk and chalkboard, dynamic geometry software can be thought of as participating in the process of generating mathematical knowledge (Borba, 2005, p. 170). However, this notion shifts the focus from technology as an amplifier, increasing the efficiency and speed of learning, to that of a reorganizer of mathematical activity (Dorfler, 1993).
When viewed as a reorganizer, technology also affects humans and human activity, changing the ways individuals interact with physical or abstract objects, complete tasks and, ultimately, the knowledge constructed (Pea, 1987). In this article we document the specific ways that VMTwG supports the collective engagement in the mathematical practices and, ultimately, individual student development of mathematical knowledge and, in particular, productive argumentative practices.
Mathematical Practices and Argumentation
Mathematics and science are often thought of as a collection of definitions, procedures, and theories to be learned and applied. In contrast to this perspective, there is a growing trend in education to focus on practices—“behavior that scientists engage in as they investigate and build models and theories” (NGSS Lead States, 2013, Dimension 1: Practices section. para. 1)—that cut across various topics. These practices, or habits of mind, which are specific to the doing of mathematics have been included in one form or another in many of the recent standards documents, including the National Council of Teachers of Mathematics’ (NCTM, 2000) Principles and Standards, the CCSS (2010), and the NGSS (NGSS Lead States, 2013). Despite language in these standards documents that indicates their importance and espouses their centrality in instruction, researchers have noted that “the brevity in which they are described and the lack of integration into the standards for mathematical content make them easy to overlook or ignore” (Reys, 2013, p. v).
In this study we focused primarily on the development of the mathematical practice of constructing viable arguments and critiquing the reasoning of others. Argumentation—using definitions and previously established results to develop conjectures and to explore and verify the truth of conjectures (NCTM Process Standard 2, CCSS Practice 4, NGSS Practice 7)—is central to mathematical reasoning and, perhaps, even its central objective (Mercier, 2011; Mercier & Sperber, 2011; Oaksford et al., 2008).
Despite their importance, argument skills are neither innately endowed nor acquired easily, and individuals of all ages perform poorly in assessments of both production and evaluation of arguments (Hahn & Oaksford, 2012; Kuhn, 1991; Oaksford et al., 2008). Research has shown that those who participate in a community identi?ed by joint activities come to share a set of standards and values that shape the behaviors central to the activity (Driver & Newton, 2000; Kuhn, Wang, & Li, 2010; Ryu & Sandoval, 2012). Thus, VMTwG capitalizes on this social and mathematical context as a catalyst for developing argumentative competence.
Existing research points to the potential of DGS at supporting students’ development of argumentation and related mathematical practices. For example, Hollebrands (2003) found that geometry students used the dragging feature of another DGS, Geometer’s Sketchpad, to justify ideas, verify conjectures, and identify aspects of a construction that remained invariant. Additional research has documented the ways in which DGS can support shifts in students’ problem solving and problem posing (Christou et al., 2005) and discovering and investigating mathematical conjectures (Habre, 2009).
Finally, a variety of researchers have observed that a DGS allows students to test and verify conjectures and begin to conceptualize arguments, justification, and proof (Arcavi, 2003; Arzarello, Olivero, Paola, & Robutti, 2002; Mariotti, 2000). We extended this work in two key ways: VMTwG is a multi-user, distributed environment (i.e., students can collaborate at a distance, mediated by the online environment), and the design of the environment and tasks allow for minimal moderation by the instructor.
Rather than viewing argumentation strictly as mathematical proof, we view argumentation more broadly as a social and sociomathematical practice that undergirds much of mathematics and mathematical development. Specifically, the negotiation of complex problems by groups of students requires mathematical sense making, planning, and perseverance (NCTM Process Standard 1, CCSS Practice 1, NGSS Practice 3) and effectively organizing and communicating ideas and critiquing the ideas of others (NCTM Process Standard 3, CCSS Practice 4, NGSS Practice 8) are all related to this broad conception of argumentation. Further, the structure of arguments is a lens that allows researchers to understand better the structure of collective activity and the development of collective mathematical understanding over time.
Toulmin’s Model: A Tool for Analyzing the Development of Mathematical Argumentation
Toulmin’s (1969) model of argumentation has been used in previous literature in both a reduced and complete form. We describe the complete model here. Toulmin’s model of argumentation consists of six types of statements, although we discuss only four in this article, Fukawa-Connelly (2014) described them as follows:
- The data (D): the foundation upon which the argument is based.
- The conclusion (C) [or claim]: that which is being argued.
- The warrant (W): justifies the relationship between the data and the conclusion.
- The backing (B): supports the warrant by suggesting why it is valid, or, put another way, explains the permissibility of the warrant. (p. 3)
We instantiate this via an argument similar to Weber and Alcock’s (2005) example:
“since x4 and 2x2 are polynomial functions, x4 + 2x2 is a polynomial function.’
In this case, the data is the first clause, the conclusion (or claim) is the second clause, and the warrant, which is unstated, would be that the sum of polynomials is also polynomial (see Figure 3).
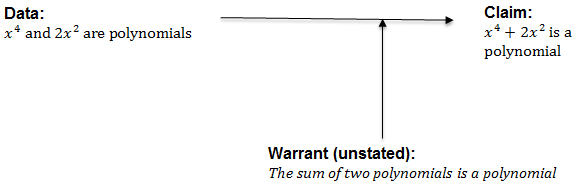
Figure 3. An illustration of a polynomial argument.
We use this method to explore individual and collective development of mathematical practices.
Multiple researchers have shown that Toulmin’s (1969) model of argumentation is helpful in analyzing classroom discourse in a mathematics classroom (Fukawa-connelly, 2014; Rasmussen & Stephan, 2008; Weber, Maher, Powell, & Lee, 2008). In particular, Krummheuer’s (1995) goal was to describe the structure of arguments produced in mathematics classrooms and the different ways that students were involved in the production of that argument. He did so by analyzing the role in the collective argument that the individual student’s contributions played. Rasmussen and Stephen (2008) further adapted Toulmin’s model as an analytical tool to look at changes in argumentation over time, for example, demonstrating the process by which conclusions become taken as shared and no longer require argumentation.
Methods
Setting and Data Collection
The setting for the current case study was VMT WinterFest 2013, which brought together (virtually) approximately 100 middle and high school students, organized into 34 teams, for online mathematics collaboration and problem solving using the VMTwG environment. Prior to the VMT WinterFest, a 13 teachers had participated in an online professional development using the VMT and materials. Those teachers then nominated students to participate, typically from their school. Each of the students was then asked to choose the pseudonym that they wanted to use throughout the project.
Teams typically consisted of students the teachers nominated. Each of the groups, which consisted of three or four students, participated in eight 1-hour VMTwG sessions (two per week for 4 weeks) scheduled at times mutually convenient for the participants. During the eight sessions, participants worked through seven topics (one topic was extended over two sessions). Each of the topics was explored in a single VMTwG session, with activities spread across multiple tasks displayed on different tabs (see Figure 4). In this study, we investigated the work of one of those teams and how it changed across the different activities.
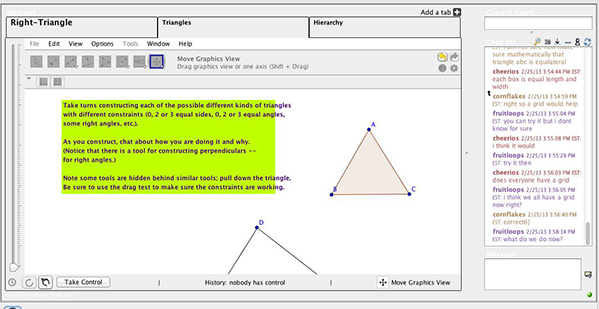
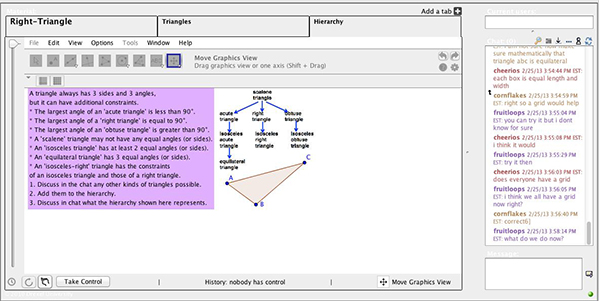 Figure 4. Tabs 2 and 3 from Session 4.
Figure 4. Tabs 2 and 3 from Session 4.
The tasks progressed from basic, such as learning how to use the tools, to creating figures that have the same properties as a given model to making explicit claims about the way figures were constructed based upon how they respond to dragging. The scope of the required constructions substantially increased over time, from triangles and perpendicular bisectors to complex polygons with specified angle relationships. In doing so, the students explored the mathematical ideas of equivalence, equidistance, and bisection via angles, lines, and circles (especially radii) and intersections.
The specific activities within each topic consisted of preconstructed drag-and-discuss tasks or open-ended construction activities (and often both). In addition, specific opportunities for reflection and topics for discussion were embedded within the activity structure. Only one student could only control the VMT environment at a time using a mouse (rather than fingers on a touchscreen). A button allows a student to take control of the tools (dragging and construction), although all students can type into the chat window at any time. See Table 1 for the specific topics addressed.
Table 1
VMTwG Topics and Tasks
Session | Topic | Tasks by Tab |
1 | Introduction to VMTwG |
|
2 | Messing Around with Dynamic Geometry |
|
3 | Visualizing the World’s Oldest Theorems |
|
4 | Constructing Triangles |
|
5 | Inscribing Polygons |
|
6 | Transforming Triangles |
|
7 | Exploring Quadrilaterals |
|
8 | Reflection and discussion. |
More information about the student activities is included in the student activity workbook (Stahl & the VMT Project Team, 2013). Most groups completed the tasks in one of the tabs during a typical session and, if time allowed, began the tasks in a second tab.
All communication and interaction within VMT is automatically recorded by the environment and can be viewed in multiple formats, including an animated video of the entire session in exactly the same format and structure as the students experienced and a transcript that recorded all VMT activity (chat postings, passes of control, the type of actions—dragging, constructing, etc.—and the coordination of GeoGebra actions and student chats). In this study, the animated recordings were used as the primary data source, and more fine-grained analysis was conducted using the transcripts.
Participants
The work of the Cereal team, consisting of three students who named themselves Fruitloops, Cornflakes and Cheerios (all pseudonyms were selected by the students when they first joined VMT) was analyzed in this study. All three students were eighth graders (about 14 years old) and participated in WinterFest 2013 as an afterschool activity. The students were beginning algebra students who had not yet taken a geometry course. WinterFest 2013 included 34 teams of middle and high school students who participated in eight dynamic geometry sessions using the VMTwG environment and supervised by their classroom teacher.
These participants were all students of the same teacher and were completing their activities in the same room. This particular group was selected for presentation in this analysis for two primary reasons; first, the communication among the group members appeared similar to that of other groups, thus suggesting that their discussions would be representative of the larger group of students. Second, they made more mathematical progress than other groups on a few of the tasks (Session 5), meaning that they had a wider range of types of problems on which they had worked.
Detailed analysis of the discourse and coconstruction of mathematical accomplishments of this group have been described in Rasmussen and Stephan (2008). In the current work, we extended the existing analysis, which focused on collaborative development and mastery of GeoGebra tools and practices such as construction and dragging, to explore the development of higher order mathematical practices, especially argumentation.
Analytical Procedures
Two foci for the current study were to analyze and explain (a) the structure of argumentation in online, collaborative VMTwG sessions and (b) how this structure evolved over time. In terms of argumentation and communication, we first began coding student discussions with regard to the ways the students responded to the mathematical prompts. We chunked chats and the student’s GeoGebra moves by the task they claimed they were working on. Within those broad chunks, lines of text from the logs of each session were coded, first to differentiate between mathematical and nonmathematical communication (such as greeting each other or time keeping), basically parsing for text relevant to the mathematical discussion.
We attempted to classify further whether the students attempted to understand or answer the question. Then, the lines of text coded as mathematical were further coded as either procedural (making statements or questions about steps to complete with no explanation) or argumentation (stating definitions, making conjectures, stating reasons, asking for reasons, asking questions to clarify meaning, etc.). For each category, specific actions (constructions), conjectures, reasons, justification, or rationale were identified, when possible.
We coded data iteratively. In particular, as we coded a student’s individual post we then reread the posts that came before and after the just-coded post. As we read the chunks of text where students were attempting to solve the problem, we described the pattern of interaction and what each line appeared to do in the interaction (e.g., responding to a question, or asking a question). That is, we read both the individual lines and the larger chunks of text and watched the GeoGebra actions to try to describe the role of the chat and action in the chunk of text.
For each session, and each chunk within a session, summary memos were written, highlighting specific interaction patterns observed as well as other theoretically significant observations and conjectures. For each session, we also noted whether the group agreed that completed the task (or acted as if they had).
Toulmin’s (1969) argumentation scheme was used to analyze further each chunk of activity. Data, claims, warrants, and backing were identified and coded. This analysis was consistent with the first stage of the research methodology prescribed by Rasmussen and Stephan (2008). Specifically, each session was repeatedly viewed using the VMT Replayer in order to get a strong sense of the data, then the data were parsed into specific student argumentations.
Each argument was coded according to Toulmin’s (1969) scheme, including the claim being made, the data to support the claim, and when given, the warrant for how the data implied the claim. In cases where no warrant was provided, conjectures or assumptions regarding implicit warrants were noted.
During each phase of analysis, all coding and interpretations were discussed within our research team until all disagreements were resolved. In general, documenting the structure and function of students’ argumentations was facilitated by the following framework. Claims are the easiest type of contribution to identify in an argumentation and consist of either an answer to a problem or a mathematical statement for which the student may need to provide further clarification. Data are less easy to document but usually involve the method or mathematical relationships that led to the conclusions.
Most times, warrants remain implied by the speaker and are elaborations that connect or show the implications of the data to the conclusion. Finally, a backing is identified typically by answering the question, “Why should I accept your argument (the core) as being sound mathematically?” Backings, therefore, function to give validity to the argumentation (Rasmussen & Stephan, 2008, p. 198). We also coded all challenges to a student’s argument by what part of the argument—the claim, data, or warrant—was challenged.
In cases where the warrant was challenged, we analyzed how the student rebutted the presented argument, noting whether this rebuttal challenged the legitimacy of the warrant itself or only argued that the warrant might not be applicable in the situation in which it was used; that is, the warrant would need to be qualified in such a way that certainty could not be obtained from its application (c.f., Inglis, Mejia-Ramos, & Simpson, 2007).
Change over time was documented by first using Toulmin’s (1969) categories to identify the existence and categorize qualities of students’ argumentation (for example, what the students treated as data for a claim). To analyze the possible changes, we created summary descriptions for each piece of an argument within each session. We then compared across the sessions looking for stable patterns and changes over time.
To organize the presentation of the results of our analyses about changes in the students’ data, warrants, and claims, we first describe early patterns and then the ways aspects of those patterns shifted over time. To describe the ways the students’ argumentation generally shifted over time (for example, becoming more abstract or general), we first created summary memos describing the interaction patterns summarized at the level of the individual arguments, and then at the level of each session describing the qualities of the arguments that the students created we also noted which students engaged in which aspects of argumentation.
To describe change over time, we paid particular attention to which students initiated what types of discussions, which students supplied what types of data and warrants, and which students supplied what types of claims. We used these descriptions to explain how the students, collectively, developed more refined norms for argumentation and, also, how the lack of teacher-moderation may have allowed what mathematicians would consider an invalid warrant.
Analysis and Results
This section presents a description of the student’s collective approach to the tasks. They began with a focus on task completion, without any justification that the task was correctly completed. As the students worked through the material, they started to offer more warrants and eventually analytic warrants in addition to the more commonly offered visual/perceptual warrants. The students worked collaboratively to accomplish the tasks that, likely, would have been beyond any of their individual abilities, and as a result, they collectively and collaboratively developed mathematically.
As an example, consider the students’ work on Topic 4 (see Stahl & the VMT Project Team, p. 20), which involved creating a right-triangle tool that they could then use to create right-triangles on demand. Each of the students began the session, noting “I’m not sure how” or “I don’t know how” to do the steps. Throughout the session, they passed control of GeoGebra back and forth. Students made 10 changes of control, with each student taking at least two turns. Each student offered at least one direction, such as “delete E” to a colleague.
At the end of the sequence of discussion and exchanges, they had successfully made a tool that would create right triangles. (For more information about the specific interaction and tool created, view the animated video on the Drexel Streams website at https://1513041.mediaspace.kaltura.com/media/VMT+Topic4/1_b0k8od55 or see the appendix for a transcript of the entire session.) The students’ were successful primarily because they were able to use the perpendicular line tool that they had experimented with earlier and then construct an additional line and delete the unneeded rays.
This activity appeared to be an example of collaborative mathematical problem solving that required each individual to contribute in order to achieve the goal. Many similar accomplishments from the Cereal group have been documented previously (c.f., Stahl, 2013a, b, 2014). Although these mathematical achievements are significant, the goal of this study was to explore further the nature of the online dialog and its role in the development of mathematical practices.
In the sections that follow, the behaviors and practices of the students in each of the sessions are described and cross-session comparisons are made as a means to identify change over time. The focus of our study moved beyond students’ accomplishing the tasks set out in the directions of each activity and explored the ways in which their argumentation structure, behaviors, and practice changed over time. This lens provided insight into another layer of mathematical development and more completely described the potential of VMTwG for supporting the development of both mathematical content and processes.
Early Focus: Completing the Tasks
One of the most important characteristics of the ways the students initially proceeded was that, especially in the first few sessions, they were focused on completing the required tasks. Their conversations in the beginning, were almost entirely about Step 1, either taking responsibility or claiming it was completed. Moreover, if the directions focused on questions, developing conjectures, or reflection, the group would regularly ignore those tasks.
Finally, when they completed a set of tasks, if the end of the allotted time was near, they would simply kill time rather than start a new prompt. Even with this completion-oriented behavior, though, the students collectively accomplished meaningful mathematics, and the way they did so changed over the course of the sessions.
Exploring Shifts in Argumentation
Claims in early sessions. In the early sessions, the students’ claims were almost entirely about completing the steps (e.g., “I did step one”). Moreover, the claimant generally offered no explanation, nor did other students request any, and results appeared to have been taken as evident. For example, after Cornflakes made the claim, “I did step one,” Fruitloops’ response was, “okay, so you can move on to step 2” (see Figure 5). Other examples of such claims included, “Done. Now someone else,” and “I did step 6.”
 Figure 5. A screen capture illustrating common interactions.
Figure 5. A screen capture illustrating common interactions.
Because the tasks in sessions 2 and 3 were often to make observations about or duplicate a particular figure and include the appropriate dependencies, the students had to develop conjectures about how the model figure was constructed. When they needed to make such observations, students simply stated them. The following are excerpts from the chat log that illustrate this tendency (throughout the paper names of points have been capitalized to conform to mathematical convention, although all of the original student work notated points in lowercase):
- “There are 4 isosceles triangles that look like a diamond.”
- “Each triangle makes 2 acute angles and one right angle.”
- “Segments DE and EC are the same length.”
- “DB and DA and BA and BC and AC I think are the same lengths.”
In all of these cases, statements and claims were simply accepted, and the students moved on to new claims or tasks. Moreover, the students did not state “it appears that…” As a result, all seven of these statements would be claims according to Toulmin’s (1969) model, since they are observational without stated data and no warrants or backing. Thus, each articulated argument appears (to take one example) as in Figure 6.
Claim:
Segments DE and EC are the same lengths
Figure 6. A model argument.
The students frequently constructed figures using the guidance and structure the VMT materials provided for them. When they attempted such constructions, they sometimes gave other students directions, such as “Make a triangle and attach two circles.” We might understand such talk as an explicit claim about how the model figure was constructed, but again, at no point in Session 2 did a student offer evidence in support of such a claim nor did any of the three colleagues ask for explanation. Thus, even this argument is considered a claim and nothing else.
In a few instances some early arguments had subtly more advanced arguments. For example, in the following excerpt is one instance where students’ claims were followed by affirmation with no discussion (all chat excerpts are reproduced exactly as typed by the students, including incorrect punctuation and spelling, except for names of points).
| Fruitloops: | when I moved point A the rest of the circles also moved which I think it shows that point C is connected to both and the same when I move point B | |
| Cornflakes: | yes | |
| Cheerios: | yeah, so it intersected both circles | |
| Cornflakes: | I see that |
In this case, Cornflakes’ statements served solely to affirm Fruitloop’s claim, as opposed to adding data, warrants, or backing or otherwise substantially improving or altering the argument.
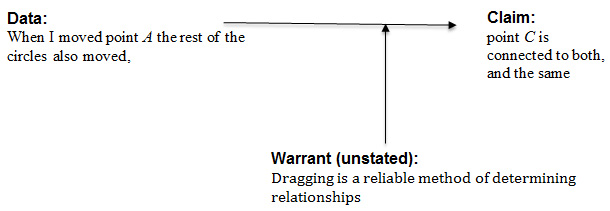
Figure 7. Modeling Fruitloop’s argument.
In addition, in this excerpt is an additional example of more complex argumentative structure: a nested argument. For example, Fruitloops noted, “okay so also when i moved point A the rest of the circles also moved which i think it shows that point C is connected to both.” In this case, she offered the claim based on observation, “when I moved point A the rest of the circles also moved,” which she then treated as data for the claim about construction: “point C is connected to both.”
This arrangement of using previous claims as data for subsequent claims was common practice by Session 2 and continued to be throughout the student’s interactions in the project. Again, though, the other students responded to this statement, “okay yes” or “yeah,” without any requests for follow-up. In a pair of cases the students included more explanation. In one interaction Fruitloops claimed that the model triangle was equilateral and invited responses:
| Fruitloops: | i think the triangle is always an equilateral. do you agree? | |
| Cheerios: | yes it is because all the sides are equal | |
| Cornflakes: | yes cause the intersection | |
| Fruitloops: | yeah even when you move any of the points like for example if i moved point B, the triangle stays equal | |
| Cheerios: | correct because its right in the middle |
In this set of interactions, the students expanded the type of statements they made. Each argument included data and a claim (“all sides are equal” implies “equilateral”) and also a statement that appeared to function to link the data and claim or support the relationship in some way—a warrant (“I moved point B”; “the triangle stays equal”).
For example, Cheerios’ statement, “correct because its right in the middle,” appears to offer an explanation that the triangle is equilateral because it is invariant under dragging. In this case the phrase, “right in the middle,” implied a fixed position and side lengths. Although this reasoning is not mathematically correct, these two cases were the first where any warrant was offered and were not representative of the interactions around the students’ claims on construction early in the VMT work. This argument might be diagramed as shown in Figure 8.
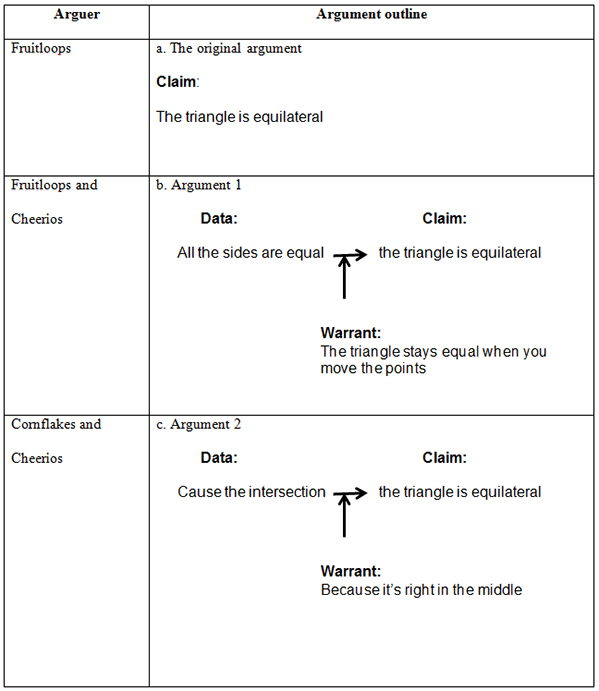 Figure 8. Argument outlines.
Figure 8. Argument outlines.
In summary, in the first sessions, the students made claims, but relatively few included a description of the data, and only two students gave explicit warrants. Only visual inspection and dragging data were presented, and each of these types apparently was accepted without question. The claims were treated as self-evident, even when the claimant was also the dragger and no other students engaged in dragging.
Dragging as collecting evidence: Trying and convincing. Session 4 began similarly to previous weeks, with each of the students taking turns performing a construction and claiming that it was complete and the other students accepting that claim with no interactions other than directive statements, such as “delete E.” However, a new type of interaction pattern emerged. After a student claimed to complete a construction, she then invited her group mates to drag the figure to test the correctness of the construction: “Someone try the drag test.”
In this case, the drag test referred to a codified set of procedures that the curriculum authors had written and named and described as a way to test whether the construction had the desired dependencies, although without explanation of why the test was effective. That is, previously, construction claims had, with one exception, been supported with purely visual evidence, but here the constructor explicitly asked the other students to collect their own evidence (dragging) in support of the claim that the construction was correctly completed. (This practice became common after its introduction here.)
On the first task in Session 7, Fruitloops made a claim about how the figure was constructed based on her dragging, and before agreeing with her claim each of the other two participants asked to drag the object themselves. This response was similar to the students’ work in Session 4, when they repeatedly passed control for dragging back and forth and individually dragged figures before agreeing on claims. In testing each of the figures, the students engaged in the same behavior. The first person would make a claim about the construction (sometimes, “I don’t know”) and others would ask to drag as well, asking, “can I get control for a sec?”
In such a series of interactions the students took up one of the primary reasons for justifying claims, that of convincing oneself and others. In a face-to-face setting, when another student is dragging with a mouse, the observers can derive nearly the same cognitive benefits. Moreover, by observing the dragging, the observers can tell whether the drag test was correctly executed and can offer suggestions about the details of the dragging movement.
In an online synchronous setting, seeing some movement of the dragged object is possible, but without access to the physical movement of the mouse (or trackpad) this means of convincing others is insufficient. Seeing how the dragger attempted to drag is not possible; only the results are visible. Thus, a request to replicate dragging can be understood as important for the requester’s thinking and conviction in a way that a request to replicate dragging in a face-to-face class is not.
When they were stating only, “I finished Step 1,” they made no attempt to convince others nor was there evidence that the students had attempted to convince themselves (although, it is reasonable to believe that they were as part of making the statement). As a result, having everyone drag was a means to promote shared conviction.
Arguing via the authority of GeoGebra. Another type of reasoning that first surfaced in Session 4 involved the students using the color that GeoGebra assigned for display of points (solid for unconstrained; light for constrained). This action represented the first claim that the students made not explicitly tied to a specific example. For example, consider the following interaction, begun by Fruitloops asking to try the drag test:
| Fruitloops: | can I try dragging it? …the lighter colored points are restricted i think? | |
| Cornflakes: | yes because they are already on the line. |
While this observation grew out of work with specific examples, the claim is stated in a general and abstract way, not tied to a specific context (the implied data would be that Fruitloops had noticed a pattern). Moreover, Cornflakes attempted to provide a warrant that justified the claim, noting “they are already on the line.”
Cornflakes may have meant that the lighter color points in this example illustrated Fruitloops’ claim because they could move only along the line and, thus, were constrained. The fact that the points were “on the line” explained why they did not move freely, that is, explaining the relationship between the data (dragging observation) and the claim. Thus, Fruitloops presented a claim, Cornflakes offered a warrant, and they immediately moved on, treating the claim as sufficiently justified. (See the argument in Figure 9.)
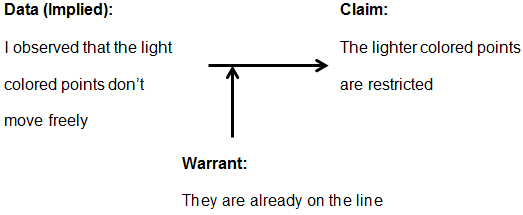 Figure 9. An outline of the argument about color.
Figure 9. An outline of the argument about color.
From this point on, the students treated the color of the point as a piece of evidence. Specifically, they took black or dark points as unconstrained and light points as constrained. In subsequent sessions, they frequently cited the color of a point when they made claims about how a model figure was constructed and as a reason why their construction did or did not match the model. The color of the point was often used as a second piece of evidence, in addition to the drag test.
One example is Cornflakes’ statement from Session 7 (Topic 13): “okay polygon 2 has all points moving except point G, and point G is also a different color.” She first asserted that her drag test suggested G was constrained, then she cited the color of the point and that it was different than the free points as an additional source of evidence. She did not restate the claim that a different color meant constrained, which we take as indicative that the understanding that color indicates constraint was taken as shared within the group. With this new type of evidence, the group had developed a more abstract reasoning process that transcended specific tasks and could be applied more generally.
The color assignment of the software became a type of argument from authority. Yet, in an important way, the drag test was also an argument based on the authority of the software. In the case of the drag test, the claim on authority was that the way a point moved when a student might drag it was reflective of the means by which it was constructed. That is, the software played fairly and appropriately reflected the constraints.
While the students explicitly negotiated whether or not they should trust this aspect of GeoGebra’s authority, they were not observed to negotiate whether GeoGebra played fair with the relationship between construction and movement under dragging nor negotiate whether the drag test fully tested needed issues.
Introducing the notion of certainty. In Session 3, the students began in much the same way as in the previous sessions but in the middle of the session, when attempting to construct a perpendicular bisector, engaged in a novel discussion (see Figure 10):
| Fruitloops: | how do we know for sure that the line is perpendicular? | |
| Cornflakes: | they’re 90 degree angles. | |
| Fruitloops: | but you can’t really prove that by looking at it. | |
| Cornflakes: | they intersect through the points that go through the circle | |
| Fruitloops: | it has to do with the perpendicular bisector |
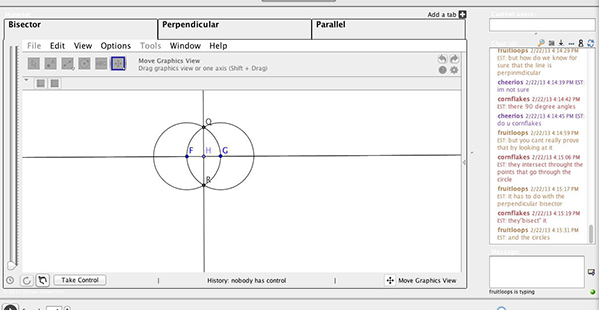 Figure 10. A screen shot illustrating the argument and state of GeoGebra.
Figure 10. A screen shot illustrating the argument and state of GeoGebra.
In previous exchanges, observational evidence would have been accepted; that is, if the angles appeared to be right angles, the students would have simply agreed and moved on. Instead, in this discussion Fruitloops continued, “but you can’t really prove that by looking at it.” This is the first instance where one of the students explicitly rejected visual evidence and instead asked for proof. The subsequent responses—Cornflakes’ claiming, “they intersect through the points that go through the circle,” and Fruitloops’ continuing, “it has to do with the perpendicular bisector”—appear to indicate some form of analytical reasoning.
Although the students did not manage to supply what mathematicians would accept as an analytical argument before they moved on to the next task, this interaction stands in contrast to previous interactions in that a student requested more than a visual warrant, and two students (including the asker) attempted to supply one.
Warrants became the object of debate. Session 4 also included an instance where the topic of what counts as a warrant for a claim became an argument of student discussion. (See video of this argument on the Drexel Streams website: https://1513041.mediaspace.kaltura.com/media/VMT_Clip_75/1_jn1397hs.) The relevant portions follow:
| Cornflakes: | so triangle ABC is an equilateral triangle | |
| Cheerios: | DEF is scalene | |
| Fruitloops: | but how do you know that all the sides are equal | |
| Cornflakes: | it looks equilateral | |
| Fruitloops: | but how can you prove it? | |
| Cheerios: | with a ruler | |
| Fruitloops: | did you measure it with a ruler? | |
| Cheerios: | yes i did | |
| Cornflakes: | sure | |
| Fruitloops: | i dont believe you | |
| Cheerios: | my finger is the ruler | |
| Fruitloops: | but you finger isnt a proper measuring tool! NOT ACCURATE! | |
| Cornflakes: | actually let me double check it | |
| Fruitloops: | how do you double check? | |
| Cornflakes: | they look pretty equal | |
| Cheerios: | yea they do the only way is to measure it i guess | |
| Cornflakes: | how do you tell? | |
| Fruitloops: | but like when we did it with the circles and their radius we could prove it becuase of the equal radii but now i dont know how we can prove that its equilateral…. | |
| Cheerios: | i think we need a line or a grid | |
| Fruitloops: | how would a crid really help? grid* | |
| Cornflakes: | I am not sure how make sure mathematically that triangle ABC is equilateral | |
| Cheerios: | each box is equal length and width | |
| Cornflakes: | right so a grid would help | |
| Fruitloops: | you can try it but i dont know for sure | |
| Cheerios: | i think it would | |
| Fruitloops: | try it then | |
| Cheerios: | does everyone have a grid | |
| Fruitloops: | i think we all have a grid now right? | |
| Cornflakes: | correct6] | |
| Fruitloops: | what do we do now? | |
| Cornflakes: | im not sure | |
| Fruitloops: | i dont know wbhat tio [what to] do i just moved it around | |
| Cheerios: | you have to line it up so point A on an intersection and then see how far away point B and C are from the line A is on | |
| Fruitloops: | yeah try to show it | |
| Cornflakes: | can you show it? | |
| Cheerios: | i just did |
The students were attempting to make a construction that matched a written model. To structure the work, Cornflakes made a claim about part of the model, “so triangle ABC is an equilateral triangle,” and Cheerios acted as if this understanding was taken-as-shared, moving to the next piece of the model. “DEF is scalene,” Cheerios responded. (DEF indicated triangle DEF, in this case, rather than shorthand for definitely, which has appeared at other points in the discussion as text-speak). Here, the claim was that triangle ABC was equilateral, but no data were offered.
Fruitloops (who had asked all such conviction questions thus far in the intervention) interrupted the discussion and asked, “how do you know that all the sides are equal?” She did not question that the triangle was equilateral; rather, she asked how the students knew that; she asked about the argument that supported the claim. Cornflakes supplied data to support her claim: “it looks equilateral.” The argument, at this point, is illustrated in Figure 11.
![]() Figure 11. The first argument.
Figure 11. The first argument.
Fruitloops responded, “but how can you prove it?” This question represented the first time in any of the sessions that the terms prove or proof were used by any of the students. By using the term she implied that the offered data were insufficient to support the claim, meaning she rejected purely visual evidence. That is, she rejected the implicit warrant that “it is possible to determine if sides are the same length by looking at them.”
Cheerios offered a potential means of proof, “with a ruler.” Fruitloops appeared willing to accept a ruler as sufficiently accurate, asking, “did you measure it with a ruler?” In this case, the data would have been, “they have the same measure,” with a warrant, of “it is possible to adequately verify that the sides are the same length via a ruler held up to the screen.”
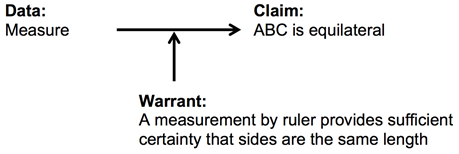 Figure 12. A revised argument.
Figure 12. A revised argument.
Both Cornflakes and Cheerios claimed that they did measure. Fruitloops responded, “I don’t believe you.” At this point the fact that all participants were sitting in the same classroom is relevant in that Fruitloops could have noticed that neither Cheerios nor Cornflakes had actually used a ruler or even had a ruler near them. Fruitloops was not arguing the warrant; rather, she questioned the data. She claimed that they did not measure.
Cheerios responded that “my finger is the ruler.” Fruitloops’ responded, “but your finger is not a proper measuring tool NOT ACCURATE!” Here, Fruitloops did not question the validity of the general warrant that a measurement by ruler provides certainty that the sides are the same length; rather, she questioned a more specific version of the warrant that related to the precision of the measurement. She appeared willing to accept a ruler, but declared that a finger is not a ruler because it is insufficiently accurate. Thus, implicitly, her warrant required some level of precision of measurement, and we revised the implied warrant to read, “a measurement by a sufficiently precise ruler provides sufficient certainty that sides are the same length.”
Cornflakes continued asserting the validity of visual evidence: “they look pretty equal.” Cheerios responded to both Fruitloops and Cornflakes, “yeah they do, the only way is to measure it I guess.” Cornflakes asked, “how do you tell?” This question was similar to Fruitloops’ initial question, so at this point all three students appeared committed to determining whether the sides only looked equal or actually were equal (seeking conviction). This assumption is one of mathematical responsibility prompted by Fruitloops’ request for proof (or valid and warranted data that supported the claim).
Fruitloops then suggested an analytic means to supply proof: “but like when we did it with the circles and their radius we could prove it because of the equal radii but now i dont know how we can prove that its equilateral….” We did not analyze the hypothetical argument but note that the data would depend on points lying on congruent circles.
Cheerios, who initially suggested measurement, did not take up Fruitloops’ claim but, rather, appeared to address Cornflakes’ question by saying, “I think we need a line or a grid.” Fruitloops asked, “how would a grid really help?” That is, Cheerios had suggested replacing the term ruler in the implied warrant (Figure 12) with a grid. Fruitloops’ question can, again, be understood as asking about the precision of the measurement (or whether the warrant was valid).
Cheerios responded to Fruitloops’ question, “each box is equal length and width,” and Cornflakes claimed that Fruitloops’ question had been sufficiently addressed: “right, so a grid would help.” Fruitloops responded, “you can try but I don’t know for sure.” They constructed a grid, and Cheerios gave directions about how to use the lattice points as measuring tools. At this point, even Fruitloops claimed, “I kind of understand,” thereby indicating acceptance of measurement via grid as a warrant. These were eighth graders; thus, mathematical proof was not a formal concept yet, but Fruitloops had during the discussion moved from suggesting a means for getting an analytic warrant to accepting measurement as a warrant for a final argument (Figure 13). Thus, in this case, the conversation actually moved her to a less mathematically sophisticated position.
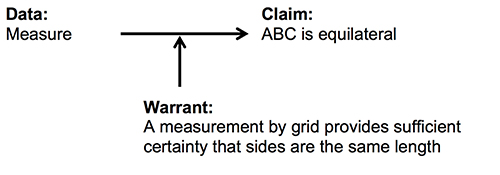 Figure 13. The final argument.
Figure 13. The final argument.
Weber, Maher, Powell, and Lee (2008) have described such discussion as powerful tools for learning about what counts as acceptable mathematical reasoning and as an important way of developing conceptual understanding of the associated content. Weber et al. hypothesized that necessary conditions for the development of such discussions included the teacher consistently asking if solutions “made sense,” giving collective responsibility for determining when a solution was correct to the students (they had to achieve consensus about whether a solution was correct) and determining how long to work on an activity.
In the VMT setting, two of the three conditions were present; the students were responsible for deciding when a task was acceptably completed, and they could work on a task for as long as they wanted, but no teachers ever asked them whether solutions made sense (the sessions were unmoderated). Moreover, the students in our sessions did not have to decide that a solution was correct. They could simply decide it was acceptable. Nor, in this case, did we explicitly require that they come to consensus; rather, it was a social norm that they all agree. In this discussion, when warrants became an object of debate, a student request for a warrant and suggestion for a means to acquire an analytical warrant were rejected in favor of measurement via a grid (where the grid was assumed to have equal side lengths by the authority of the software). Finally, the students never explicitly discussed the level of precision needed to satisfy the warrant; rather, they accepted both a ruler and a grid as providing sufficient precision without conversation.
Giving reasons becomes a normal activity. By Session 5, the students started to treat explanation and justification as a normative activity and were more explicit about the data for the claims. During the second half of session 5, the group started to treat warrants as normative rather than as isolated instances, such as in the two discussions shown previously, making them more explicit and drawing on a wider variety for their claims. They attempted to decide how a triangle had been constructed (Figure 14).
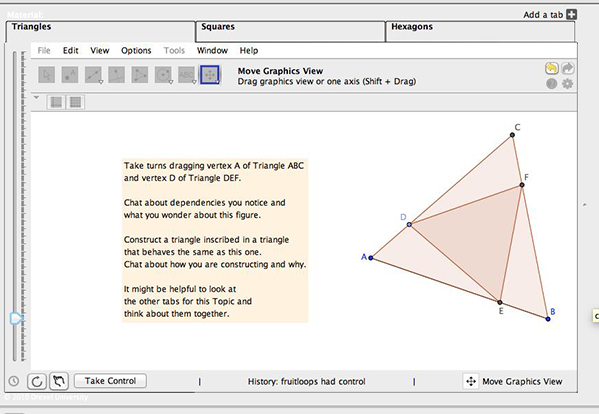 Figure 14. The triangle task, after the students had dragged points.
Figure 14. The triangle task, after the students had dragged points.
Fruitloops: yeah when you move vertex A, the inner triangles changes size but never shape Cheerios: when you move vertex A triangle DFE don’t move at all it just becomes smaller when you shrink the big triangle and vice versa.
| Fruitloops: | yeah when you move vertex A, the inner triangles changes size but never shape | |
| Cheerios: | when you move vertex A triangle DFE don’t move at all it just becomes smaller when you shrink the big triangle and vice versa. |
Moreover, in Session 5, the students were explicit about the behavior of each point in the model figure. When a point was not mentioned, or even when it was part of a figure a colleague had described, students asked follow-up questions to clarify. Fruitloops asked, for example, “what about point E?” even though point E was part of the triangle that Cheerios had just described. That is, in Session 5 the students regularly provided more explicit statements regarding the data for claims, asking for more thorough (or clear) statements of the behavior of the figure, responding to such questions and, as a result, having richer discussions about the model figures.
Moreover, they adopted appropriate mathematical terminology and naming conventions, such as naming triangles by the vertices (except for the phone-texting convention of not using capitalization), using the term vertex regularly and correctly (as opposed to referring to everything as an undistinguished point, as they did in earlier sessions), and correctly using the term equivalent to describe congruent triangles.
In terms of providing warrants and warrant seeking behavior, the second half of Session 5 saw a marked change. Two students asked for further justification, and the other students’ first reaction was to attempt an analytical and dragging-based explanation so that the relationship between the dragging behavior and the claims were double warranted. One such interaction can be viewed at the Drexel Streams website: https://1513041.mediaspace.kaltura.com/media/VMT_Clip_76/1_ql4gppjt.
The video shows students justifying a series of claims Cheerios and Conflakes had made about multiple construction steps that included producing points M and R, as follows:
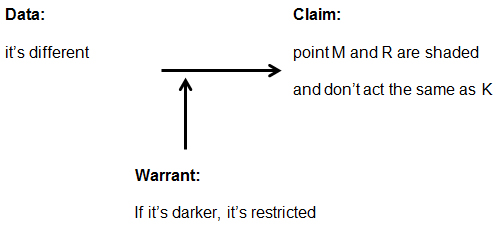
| Fruitloops: | so then why are point M and R shaded dark and don tact [don’t act] the same as K? | |
| Cheerios: | it’s different. | |
| Fruitloops: | BUT WHY??? | |
| Cornflakes: | yeah if its a darker its restricted i think. | |
| Fruitloops: | but why are M and R restricted but K isnt? | |
| Cornflakes: | because the invisible circles are still there | |
| Fruitloops: | okay so its because we made K by just using the point tool and putting it on the line but with M and R we made it through using circles so technically, the circle is still there but its hidden but we just don’t see it. |
In this interaction, Fruitloops asked a question, then Cheerios asserted, “it’s different,” which would result in the argument shown in Figure 15.
 |
| Figure 15. An outline of the current argument. |
In this interaction, Fruitloops asked a question, then Cheerios asserted, “it’s different,” which would result in the argument shown in Figure 15.
 Figure 15. An outline of the current argument.
Figure 15. An outline of the current argument.
Fruitloops refused to accept that argument as sufficient, and Cornflakes responded by making explicit the understanding about the color of points (Figure 16).
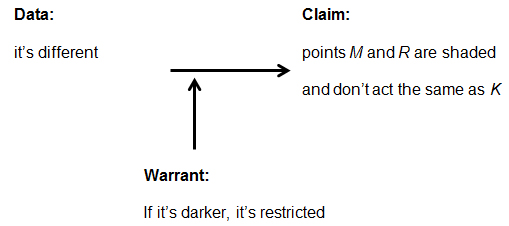 Figure 16. An outline of the next step of the argument.
Figure 16. An outline of the next step of the argument.
Fruitloops persisted in asking for an explanation, which in this case, appeared to reject as insufficient this previously accepted type of warranting. Cornflakes interpreted this request as asking for an analytical explanation and responded in a way that we took to mean, “We put the points on circles that are now invisible and that is restricting the places where you can drag M and R.”
Fruitloops then took the short statement that Cornflakes made and made more explicit the claims on the construction of the circles and made explicit why the construction order would constrain the points (thus, GeoGebra assigned a lighter color), and the argument is as shown in Figure 17. All of the students explicitly agreed with this elaborated statement.
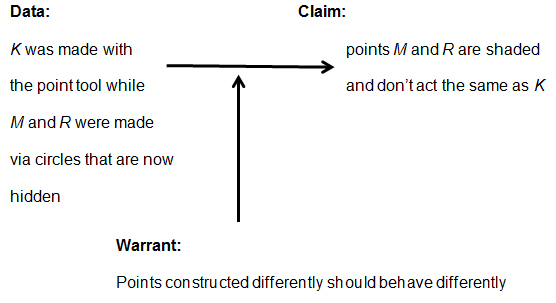 Figure 17. Final state of the argument.
Figure 17. Final state of the argument.
Another similar instance involved an exchange between Cheerios and Fruitloops, but in this case Fruitloops offered an unprompted warrant.
| Cheerios: | the distance between M and J is the same between OK and LN and PI. | |
| Fruitloops: | I saw and I understand. … all the radii are the same so the distances from KO, LN, and IP, and IM are the same. |
As was common in previous sessions, Cheerios offered no statement of the data or any other explanation, and Fruitloops’ response agreed and elaborated by providing analytic data in addition to Cheerios’ observational data (Figure 18).
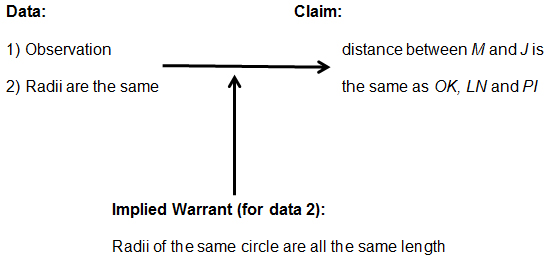 Figure 18. The combined argument of Cheerios and Fruitloops.
Figure 18. The combined argument of Cheerios and Fruitloops.
In the first of these conversations, Fruitloops appeared initially not to understand why Cheerios and Cornflakes’ claims were correct, and as a result, wanted an analytical statement to explain. In the second conversation, Fruitloops appeared immediately to understand the claim and appeared to offer analytical data, with the implied warrant that the radii of a circle are all the same distance, to justify it. That is, her behavior in the first conversation asked and elaborated for explanatory purposes and in the second elaborated for convincing purposes.
Moreover, Fruitloops was able, in each case, to provide an analytical statement of data and, thus, appeared to have a more abstract understanding of the situation than did Cornflakes and Cheerios. Yet, in the first conversation she appeared unable to determine how to make a construction or interpret the results, and in the second, she may not have thought to offer the statement about equality without Cheerios’ initial claim.
By Session 7, in terms of argumentation, the students always included more complicated claims, such as, “when you move E, G moves away or closer to F. so I think G is definitely constrained and G moves whenever you move point E and F but it doesnt move when you move H.” In this case, Fruitloops explicitly named the points, described the behavior that she observed under dragging, and then described the one point as constrained. That is, compared to earlier sessions, they were much more explicit about the data on which they based their claims of being constrained. The dragging task they worked on is shown in Figure 19.
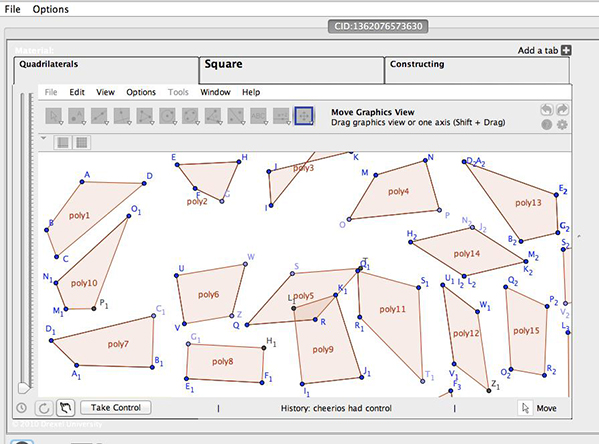 Figure 19. The dragging task of Session 7.
Figure 19. The dragging task of Session 7.
Past constructions became reasons to support hypotheses about construction. In their discussion, students more explicitly described their conjectures about construction by linking them to previous experience, which happened in three cases. One such exchange follows:
| Fruitloops: | how was it made? | |
| Cornflakes: | L some points are dependent on others maybe some invisible circles and the shapes could be dependent on thos circles | |
| Cheerios: | yeah, maybe like the triangles (Session 5). | |
| Fruitloops: | maybe because point G only moves in a circular motion around point F. | |
| Cornflakes: | yeah and one of the points was on the circle: | |
| Cheerios: | remember when we made the triangle the same thing happened. | |
| Fruitloops: | but i dont really know how it could have been made? | |
| Cheerios: | maybe they used another shape instead of circles. | |
| Cornflakes: | we coulda had a shape on a triangle or square made it invisible but in reality the other shape is still there therefore making one of the points that was on the shape dependent on that shape. |
Fruitloops asked a question, Cornflakes responded, and Cheerios immediately linked to past constructions. Fruitloops then agreed and provided a more explicit description of the movement of point G as additional evidence in support of the claim. Cornflakes continued discussing the construction in Session 5. Because Fruitloops continued to question the construction idea, even with the addition of the claims about the hidden circles, Cheerios and Cornflakes proposed a modification of the previous idea of hidden circles.
This technique appears to have been Cheerios’ on-the-spot invention, in that the students had never before done such a construction. Cornflakes’ final statement indicates they had become able to use the tools flexibly and creatively.
Discussion
The goal of this investigation was to show the promise of VMTwG in supporting the development of argumentation and the mathematical practices. This study explored the Cereal group’s collaborative work in the VMTwG environment and used the lens of argumentation to explore how their mathematical activity changed across the eight sessions. We demonstrated that they were persistent problem solvers. They were task oriented, especially during the first few sessions, but they would work to complete the tasks even when they were difficult and none of the students, individually, knew how to do so. This collaborative engagement appeared to support their continued engagement, because it allowed intellectual responsibility to be passed back and forth between the students.
Over the course of the eight sessions the students changed the way they described their ideas and argued about the mathematics. First, the way the students described their observations of the effects of dragging on figures changed. In the first sessions they made short statements that typically described only single points and often skipped data and moved directly to claims about construction (“It’s not restricted”).
By the last sessions, the students made complex claims about their dragging observations, describing the movement of the point being dragged as well as other nearby points and, as appropriate, the variance or invariance of the figures of which the points were part. These changes also supported more complex claims about figure construction and the development of more abstract ways of reasoning about the constructions, even without active moderation by teachers or VMT team members.
In the first few sessions, the students accepted without question the unstated perceptual warrants of dragging behavior or simply that “it looks like…” They quickly realized that GeoGebra used different colors to indicate whether points were constrained by construction or able to move freely. They engaged in a discussion about this point and came to an agreed-upon conclusion. Their evidence was pattern recognition. This reasoning is not necessarily the type we want students to use, as it is essentially arguing from authority. It is, however, more abstract than the dragging evidence or the “it looks the same” perceptual evidence that they had previously used, in that it was about constructions and generalized patterns of behavior.
While these two forms of reasoning were the most common, the students engaged in analytic reasoning a number of times, making claims about equality of distances via the radius of a circle, as an example. Yet, without moderation students might accept an authoritative visual argument; measuring with a ruler or grid. Fruitloops did not appear to trust this data, but both Cheerios and Cornflakes did. As a result, Fruitloops allowed it even though the conversation included allusions to previous arguments that they had settled analytically.
Even though the students may not have moved to accepting only analytical arguments, they increased the number of types and sophistication of the arguments in which they engaged. Moreover, their communication became more complex and more mathematical, and they more frequently engaged in discussions about thinking as opposed to making simple statements of procedures.
This case study, therefore, demonstrated the promise of the online, multi-user VMTwG intervention to develop students’ mathematical and argumentative practices. The students were also able to do so in a timeframe that was limited in comparison to the standard mathematics class. The ability to see and do constructions, to experience dragging in real time and concurrently participate in a chat session were critical features in the collective mathematizing and development and normalizing of argumentation.
The primary limitation of this study is that it was a case study investigating a single group’s work as part of a single intervention (the VMT). While the ways these students engaged in the tasks may be broadly representative of the population of students in the project more generally, these students were more capable in terms of the mathematical content than most of the groups of students. Moreover, this intervention was of a limited duration and was not designed to track lasting change nor designed for transfer of the mathematical practices, only close transfer of the mathematical ideas within the tasks. Thus, we do not claim lasting change on the students, nor that they more consistently engaged in mathematical argumentation in other areas.
Because of the exploratory nature of this study, the conclusions we drew are tentative in terms of generalizability and should be backed with additional study. This type of exploratory work, however, is needed in order to determine whether broader study is appropriate. As a result, we see multiple ways to build on this study.
In particular, the primary areas for further study are those areas identified in the limitations. The VMT has promise for improving student development of argumentation and the mathematical practices, but further investigations of the relationship between task design, including the prompts given to students and the structuring of the mentoring, could make substantial improvements in the resulting outcomes. Although a potentially controversial assertion, the value is in the development of the mathematical practices rather than the specific mathematical content that the students learned.
Finally, we intend to explore across other similar interventions the importance of synchronous versus asynchronous collaboration and, as technology improves, video-based interaction versus the text-based interaction that the VMTs used. The particular medium, writing out of all text, stripped of gesture, tone, and facial expression (although teenagers are remarkably good at conveying tone via text) might be one of the important features in the development of communication via necessitating more complete thoughts, rather than simply, “you know.”
A final area of further study is the role of more active moderation in student development. In the era of massive open online courses and cost-effective education, the idea of unmoderated or minimally moderated courses is appealing. Certainly, the more detailed descriptions and more complex arguments indicate that potential exists for such environments. However, both the role of online presence and moderation (and the role of the teacher, in general, in environments such as this)—for supporting additional development as well as more efficient development—and professional development for teachers that could scaffold such moderation are worthy of further investigation.
The results in this paper have multiple implications for teacher preparation. Most obviously, teachers—like students—often have little experience with argumentation, and our results and potential for the development of argumentation skills and practices via logic extend to teacher professional development settings. In addition, previous research with VMT has shown that working within collaborative dynamic geometry environments has the potential to (a) overcome past negative experiences with dynamic geometry and enable teachers to envision using dynamic geometry in their classes and (b) allow teachers to experience mathematical collaboration and overcome their resistance toward group work (Grisi-Dicker, Alqahtani, & Powell, 2013).
We have also found that when teachers are working at a distance, they are more explicit and precise (as expressed by the Standards for Mathematical Practice in the CCSS) in their communication than when we have worked with them in person, using fewer pronouns (e.g., this, that) and more nouns with named points (e.g., line AB), as appropriate.
More generally, access to the logs of their work and the replayer allows teachers to be more reflectively aware of their own development and to develop more specific trajectories for their students. Previous research (Bartell, et. al, 2013) has found that teachers over-attribute conceptual understanding to students. With the complete record of student work and communication, however, we are able to ask the teachers to defend their claims via the student work. This level of transparency enables teachers to argue about what the evidence is and how to appropriately interpret it, two important skills that are consistent with recent work in teacher professional noticing (cf., Jacobs, Lamb, & Philipp, 2010).
In short, while in this paper we documented the potential of VMT for supporting the development of argumentation skills and practices, the VMT environment can also be a rich environment for teacher learning and development—in argumentation, mathematical content more broadly, and pedagogy.
Finally, we note the importance of helping teachers understand the affordances and constraints of this type of technology for working with their students. For example, in addition to the difference between static and dynamic geometry, what does the fact that all interaction is via text mean for student learning? How does it change the way that they engage and interact with each other? How can it be used to plan classes that develop a wider range of student mathematics and mathematical practices? These are questions that still need investigation, but also indicate the transformative potential of the VMT and online mathematical interactions, more generally.
References
Arcavi, A. (2003). The role of visual representations in the learning of mathematics. Educational Studies in Mathematics, 52(3), 215-241. doi: 10.1023/A:1024312321077
Arzarello, F., Olivero, F., Paola, D., & Robutti, O. (2002). A cognitive analysis of dragging practices in Cabri environments. Zentralblatt für Didaktik der Mathematik, 34(3), 66-72. doi: 10.1007/BF02655708
Bartell, T. G., Webel, C., Bowen, B., & Dyson, N. (2013). Prospective teacher learning: Recognizing evidence of conceptual understanding. Journal of Mathematics Teacher Education, 16(1), 57-79.
Borba, M. C. (2005). The transformation of mathematics in on-line courses. In H. Chick & J. Vincent (Eds.), 29th Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 169-176). Melbourne, Australia: PME.
Borba, M. C., & Villarreal, M. E. (2005). Humans-with-media and the reorganization of mathematical thinking: Information and communication technologies, modeling, visualization and experimentation. New York, NY: Springer Science+Business Media.
Christou, C., Mousilides, N., Pittalis, M., & Pitta-Pantazi, D. (2005). Problem solving and problem posing in a dynamic geometry environment. The Montana Mathematics Enthusiast, 2(2), 125-143.
Cobb, P. (2000). Conducting Teaching experiments in collaboration with teachers. In R. A. Lesh & E. Kelly (Eds.), New methodologies in mathematics and science education. Dordrecht, NE: Kluwer.
Cobb, P., & Bauersfeld, H. (1995). The emergence of mathematical meaning: Interacting in classroom cultures. Hillsdale, NJ: L. Erlbaum Associates.
Cobb, P., Stephan, M., McClain, K., & Gravemeijer, K. (2001). Participating in classroom mathematical practices. Journal of the Learning Sciences, 10, 113-164.
Cobb, P., & Yackel, E. (1996). Constructivist, emergent, and sciocultural perspectives in the context of developmental research. Educational Psychologist, 31(3/4), 175-190.
Common Core State Standards Initiative. (2010). Common core state standards for mathematics. Retrieved from http://www.corestandards.org/assets/CCSSI_Math Standards.pdf
Dorfler, W. (1993). Computer use and views of the mind. In C. Keitel & K. Ruthven (Eds.), Learning from computers: Mathematics education and technology. Berlin, DEU: Springer Verlag.
Driver, R., & Newton, P. (2000). Establishing the norms of scientific argumentation in classrooms. Science Education, 84(3), 287.
Fukawa-connelly, T. (2014). Using Toulmin analysis to analyse an instructor’s proof presentation in abstract algebra. International Journal of Mathematical Education in Science and Technology, 45, 75-88. doi: 10.1080/0020739X.2013.790509
Grisi-Dicker, L., Alqahtani, M., & Powell, A. (2013). Mathematics learning across the professional life span: Learning with dynamic geometry in a collaborative, discursive, and online environment. A. M. Lindmeier & A. Heinze (Eds.), Proceedings of the 37th conference of the International Group for the Psychology of Mathematics Education (Vol. 5, p. 231). IPN Leibniz-Institut fd Pädagogik d. Naturwissenschaften an d. Universität Kiel: PME
Habre, S. (2009). Geometric conjectures in a dynamic geometry software environment. Mathematics & Computer Education, 43(2), 151-164.
Hahn, U., & Oaksford, M. (2012). Rational argument. In K. Holyoak & R. Morrison (Eds.), The Oxford handbook of thinking and reasoning (2nd ed.; pp. 277-299). Oxford, UK: Oxford University Press.
Hollebrands, K. F. (2003). High school students’ understandings of geometric transformations in the context of a technological environment. The Journal of Mathematical Behavior, 22(1), 55-72. doi: doi.org/10.1016/S0732-3123(03)00004-X
Inglis, M., Mejia-Ramos, J. P., & Simpson, A. (2007). Modelling mathematical argumentation: The importance of qualification. Educational Studies in Mathematics, 66(1), 3-21.
Isiksal, M., & Askar, P. (2005). The effect of spreadsheet and dynamic geometry software on the achievement and self-efficacy of 7th-grade students. Educational Research, 47(3), 333-350.
Jacobs, V. R., Lamb, L. L., & Philipp, R. A. (2010). Professional noticing of children’s mathematical thinking. Journal for Research in Mathematics Education, 169-202.
Krummheuer, G. (1995). The ethnography of argumentation. In P. Cobb & H. Bauersfeld (Eds.), The emergence of mathematical meaning: Interaction in classroom cultures. Hillsdale, NJ: Lawrence Erlbaum Associates.
Kuhn, D. (1991). The skills of argument. New York, NY: Cambridge University Press.
Kuhn, D., Wang, Y., & Li, H. (2010). Why argue? Developing understanding of the purposes and values of argumentative discourse. Discourse Processes, 48(1), 26-49.
Mariotti, M. (2000). Introduction to proof: The mediation of a dynamic software environment. Educational Studies in Mathematics, 44(1-2), 25-53. doi: 10.1023/A:1012733122556
McClain, K., & Cobb, P. (2001). The development of sociomathematical norms in one first-grade classroom. Journal for Research in Mathematics Education, 32(3), 236-266.
Mercier, H. (2011). When experts argue: Explaining the best and the worst of reasoning. Argumentation, 25(3), 313-327. doi: 10.1007/s10503-011-9222-y
Mercier, H., & Sperber, D. (2011). Argumentation: Its adaptiveness and efficacy. Behavioral and Brain Sciences, 34(2), 94-111. doi: doi.org/10.1017/S0140525X10003031
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
NGSS Lead States. (2013). Next generation science standards: For states, by states. Washington, DC: The National Academies Press.
Oaksford, M., Chater, N., & Hahn, U. (2008). Human reasoning and argumentation: The probabilistic approach. In J. Adler & L. Rips (Eds.), Reasoning: Studies of human inference and its foundations (pp. 383-413). Cambridge, UK: Cambridge University Press.
Pea, R. (1987). Cognitive technologies for mathematics education. In A. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 89-122). Hillsdale, NJ: Lawrence Erlbaum Associates.
Rasmussen, C. L., & Stephan, M. (2008). A methodology for documenting collective activity. In A. E. Kelly, R. A. Lesh, & J. Y. Baek (Eds.), Handbook for innovative design research in science, technology, engineering, and mathematics (STEM) education (pp. 195-215). New York, NY: Taylor & Francis.
Reimer, K., & Moyer, P. S. (2005). Third-graders learn about fractions using virtual manipulatives: A classroom study. The Journal of Computers in Mathematics and Science Teaching, 24(1), 5-25.
Reys, B. (2013). Foreward. In Koestler, C., Felton, M.D., Bieda, K., & Otten, S., (Eds.), Connecting the NCTM process standards and the CCSSM practices (pp. v-viii). Reston, VA: The National Council of Teachers of Mathematics.
Ryu, S., & Sandoval, W. A. (2012). Improvements to elementary children’s epistemic understanding from sustained argumentation. Science Education, 96(3), 488-526. doi: 10.1002/sce.21006
Stahl, G. (2009). Studying virtual math teams. New York, NY: Springer.
Stahl, G. (2013a). Seminar: Analyzing virtual math teams enacting geometric practices [Electronic slideshow]. Presented at the LinCS Seminars, University of Gothenburg, Sweden. Retrieved from http://GerryStahl.net/pub/analyzing.pdf
Stahl, G. (2013b). Translating Euclid: Designing a human-centered mathematics. San Rafael, CA: Morgan & Claypool Publishers.
Stahl, G. (2014, November). The display of learning in groupwork. Paper presented at the Association for Computing Machinery Conference on Supporting Groupwork (GROUP 2014), Sanibel Island, FL.
Stahl, G., & the VMT Project Team. (2013). Topics in dynamic geometry for virtual math teams. Retrieved from http://gerrystahl.net/vmt/topics.pdf
Toulmin, S. (1969). The uses of argument. Cambridge, UK: Cambridge University Press.
Weber, K., & Alcock, L. (2005). Using warranted implications to understand and validate proofs. For the Learning of Mathematics, 25(1), 34-38, 51.
Weber, K., Maher, C., Powell, A., & Lee, H. (2008). Learning opportunities from group discussions: Warrants become the objects of debate. Educational Studies in Mathematics, 68(3), 247-261. doi: 10.1007/s10649-008-9114-8
Working Group on the Common Core State Standards. (2011). The Common Core State Standards and teacher preparation: The role of higher education. Washington, DC: Science and Mathematics Teacher Imperative/Association of Public and Land-Grant Universities.
Author Notes
Tim Fukawa-Connelly
Drexel University
Email: [email protected]
Jason Silverman
Drexel University
Email: [email protected]
![]()