Documenting Collective Development in Online Settings

The necessary blend of content and process called for in the National Council of Teachers of Mathematics’ (2014) Principles to Action necessitates instructional practices that are “complex, demanding, uncertain, and not reducible to predictable routines” (Cobb, Zhao, & Dean, 2009, p. 167).  One social resource for supporting teachers as they attempt to develop demanding instructional practices of this type is participation in strong professional networks.  Ongoing reform efforts in a number of content areas, including mathematics, have focused on teachers’ activities as they participate in and contribute to the development of professional teaching communities (e.g., Achinstein, 2002; Franke & Kazemi, 2001; Grossman, Wineburg, & Woolworth, 2001; Kazemi & Franke, 2004; Little, 2002; Nickerson & Moriarty, 2005; Stein & Brown, 1997; Warren & Rosebery, 1995; Westheimer, 1998) .

Our current research was grounded in an extended research project focused on supporting online professional development. The goal of this design-research based project was to engineer and study the ways in which the interactive and collaborative nature of the Internet can support mathematics teacher development.

This paper describes a methodology for studying the emergence of collective ways of interacting and reasoning and how these collective norms support or constrain individual development in an online environment.  An overview of work with communities in teacher education is provided, followed by a description of the salient aspects of two analytical frameworks developed for studying collective learning for face-to-face environments.  A framework is then proposed that builds on these existing analytical frameworks yet is sensitive to the unique nature of online interaction.  One example analysis is presented, which provides additional detail about specific stages of analysis and highlights the potential implications of this work.

Studying Communities in Teacher Education

Naturally, we want to follow the current efforts at teacher professional growth that focus on the need to support the development of communities of teachers that can both nurture and sustain generative growth (as described by Franke, Carpenter, Levi, & Fennema, 2001; Nelson & Hammerman, 1996; Wilson & Berne, 1999). This generativity means not only maintaining new practices over time, but also modifying and adapting practices continually in response to new learning and reflection. Franke et al. (2001) argued that both maintaining practice and generativity can be observed at the level of individual teacher, but a crucial difference between the two is that generativity occurs in the context of collaborative inquiry rather than in isolation.

From a theoretical standpoint, what remains constant throughout the discussion of communities of teachers in the research literature is the social situatedness of teachers’ learning within the activities of these communities (Franke & Kazemi, 2001; Grossman, Wineburg, & Woolworth, 2000; Lehrer & Schauble, 1998; Rosebery & Warren, 1998; Stein, Silver, & Smith, 1998; Warren & Rosebery, 1995) .  This emphasis on social situatedness is consistent with Rogoff’s (1994) claim that “learning and development occur as people participate in the sociocultural activities of their community” (p. 209).  Therefore, if a community is the context in which teachers are developing these new practices, it follows that the community of teachers and the teachers’ diverse ways of participating should be taken as a unit of analysis.

Thus, the focus is on the communal practices that are the social context for the learning of the teachers, which is not to say that the individual is no longer important or that teacher diversity does not exist.  Quite the contrary, this diversity of the individual members of a community is a primary resource on which to capitalize in supporting the collective learning of the community, as no single member of any community possesses all the knowledge needed.

In an effort to document collective ways of interacting and reasoning in online settings, we started with frameworks used in face-to-face environments to investigate the ways in which they were (or were not) transferable.  Rasmussen and Stephan’s (2008) methodology for documenting collective activity proved useful as a starting point.  Using an argument as the unit of analysis and Toulmin’s (1969) model to describe the structure and function of various components of an argument, Rasmussen and Stephan (2008) described a three-phase approach to documenting collective activity.

Phase 1 involves the creation of an argumentation log, where arguments are identified and documented through claims, data, warrants, and backing.  Phase 2 involves looking across the arguments in the argumentation log and identifying instances when (a) backings or warrants become implied without challenge or the challenge is rejected or (b) any of the four parts of an argument (data, warrant, claim, or backing) changes function without challenge or a challenge is rejected. Finally, Phase 3 of the methodology involves organizing the identified collective activity around particular mathematical practices.

Although a powerful analytical tool, Rasmussen and Stephan’s (2008) framework is limited in the assumption that the group being analyzed is already a community. This assumption is not necessarily the case when examining groups of teachers online, where normative ways of participating and reasoning have not yet been established.  Dean (2005) developed an analytical framework that specifically focused on the collective learning of a group of teachers as they emerged into a professional teaching community.  Dean (2005) emphasized the importance of differentiating between a group of teachers who meet to work on issues of mutual interest and a professional teaching community.  Therefore, we are cautious about the use of the word community when discussing our research.

Researchers who have collaborated with groups of teachers to establish communities (Franke et al., 2001; Grossman et al., 2001; Warren & Rosebery, 1995) have clarified that a group of teachers who collaborate with each other in some way does not necessarily constitute a community.  Thus, until the characteristics of a community emerge and can be documented, we refer to our group of teachers as a collective (for criteria for distinguishing a group from a community see Gamoran et al., 2003; Lave & Wenger, 1991; Newmann & Associates, 1996; Rogoff, 1995; Secada & Adajian, 1997; Wenger, 1998) .

While developing her analytical framework, Dean (2005) identified qualitatively distinct types of norms based on a review of literature on teacher change.  As a result, the framework initially focused on three types of norms: (a) norms of general participation, (b) norms of pedagogical reasoning, and (c) norms of mathematical reasoning. Dean’s retrospective analysis of the collective learning of the teacher group throughout the design research experiment to test the adequacy of the three norms delineated a priori via literature review revealed that all three types of norms were relevant in analyzing the collective learning of the teacher group. However, the framework had to be modified to include a fourth type of norm that emerged as relevant: norms of institutional reasoning.  Naturally, these four types of norms did not evolve independently.  Rather, the evolution of one type of norm created conditions within the group for the evolution of norms of another type.

Dean (2005) identified norms by discerning patterns or regularities in the ongoing interactions of the members of the developing teaching community.  A norm is, therefore, not an individualistic notion but is instead a joint or collective accomplishment of the members of a community (Voigt, 1995). A primary consideration when conducting analyses of this type is to be explicit about the types of evidence used when determining that a norm has been established so that other researchers can monitor the analysis.

First, building on Rasmussen and Stephan’s (2008) work, a relatively robust type of evidence occurs when a particular way of reasoning or acting that initially has to be justified is itself later used to justify other ways of reasoning or acting.  In such cases, the shift in the role of the way of reasoning or acting within an argument structure from a claim that requires a warrant to a warrant for a subsequent claim provides direct evidence that it has become normative and beyond justification.

A second, robust type of evidence is indicated by Sfard’s (2000) observation that normative ways of acting are not mere arbitrary conventions for members of a community that can be modified at will. Instead, these ways of acting are value-laden in that they are constituted within the community as legitimate or acceptable ways of acting.  This observation indicates the importance of searching for instances where a teacher appears to violate a proposed communal norm in order to check whether his or her activity is constituted as legitimate or illegitimate.

In the former case, the conjecture that a particular activity was normative would need to be revised; whereas, in the latter case the observation that the teachers’ activity was constituted as a breach of a norm would provide evidence in support of the conjecture (cf., Cobb, Stephan, McClain, & Gravemeijer, 2001).

Finally, a third and even more direct type of evidence occurs when the members of a professional teaching community talk explicitly about their respective obligations and expectations. Such exchanges typically occur when one or more of the members perceive that a norm has been violated.

This type of evidence for establishing a normative way of reasoning that builds on Sfard’s (2000) observation was problematic when documenting the emergence of the norms of general participation.  Any claim about emerging norms based on one person challenging another’s assertion must necessarily be tentative until challenging itself becomes a general participation norm of the group.

In an effort to establish certain types of participation as normative, Dean (2005) started her investigation of norms of general participation with a count analysis of each utterance to establish how often a person made an utterance, who the utterance was directed toward (another teacher or the facilitator), and the type of utterance (mathematical, pedagogical, or institutional).

Transitioning to Communities in an Online Context

These types of frameworks were developed to document the emergence of norms within a group interacting in a face-to-face setting.  Our challenge with this project has been determining if and how aspects of existing analytical frameworks created for face-to-face environments are transferrable to online environments, specifically asynchronous.

As with the face-to-face environments, we were still interested in analyzing the collective learning of teachers.  Thus, the collective remains the unit of analysis.  Also similar to face-to-face environments, there is no guarantee that all participants who are present are attending to the conversations, so claims are made based on utterances or the lack there of.  Further, in the online environment, participants may not have read all other posts.  Much like being present in a face-to-face does setting does not guarantee engagement, merely being logged on to a forum is not evidence of engagement in a particular discussion.  Thus, posts to discussion forums are used as data to document the emergence of normative practices.

Although to our advantage, challenging as a general participation norm appears to be more palatable online, with little evidence of participants “playing community” (Grossman et al., 2001). Online participants are more willing to engage their peers actively than in face-to-face seettings (Smith & Ferguson, 2002) and to question others’ contributions and to defend and justify their own (Wojnar, 2002). However, the frequency with which a person made an utterance, toward whom the utterance was directed, and the type and function of the utterance still need to be established.

The first two of these factors can be analyzed using a variant of Dean’s (2005) utterance count analysis.  However, due to the structure and use of online discussions, additional analysis is needed to determine clearly the details of participation and interaction in the online space. When a participant makes a post in a specific thread within a discussion board, for example, it is often unclear to whom it is directed. Further, it is also unclear who reviews each post, as participants may scroll through or mark posts as “read” without actually reviewing them. Whether the post can be used as evidence of a collective accomplishment is, thus, unclear .

We used social network analysis (SNA), a mathematical approach for analyzing interactions and exploring human and social dynamics, to better understand the intricacies of online interactions. Grounded in the mathematical discipline of graph theory, SNA allows researchers to create visual representations of the structure of social network and the strength of the ties between actors in the network (Wasserman & Faust, 1994). A variety of others have used SNA to understand and explore online collaborative settings such as an online course (Penuel & Riel, 2007; Penuel, Sussex, Korbak, & Hoadley, 2006; Su, Bonk, Magjuka, Liu, & Lee, 2005) .

In particular, SNA allowed us to quantify individuals’ prominence in the collaborative setting and to identify specific collectives within an online class for analysis. SNA techniques allow researchers to identify particularly cohesive groups and to explore the characteristics of these collectives. Chen, Zaïane, and Goebel (2009) proposed the method of iterative local expansion to identify local communities that may have properties that are quite different from the properties of the entire network. They used the term community differently than we do. What they referred to as communities or local communities, we refer to as cohesive collectives. Our current research agenda centers around documenting whether these cohesive collectives begin to display characteristics of communities of practice.

Chen et al.’s (2009) method involves beginning with a particular node (or individual) and exploring all the neighbors of the given node. Then, the “local community” is identified by optimizing the proportion of internal edges (connections between members of the local community) and the total number of edges adjacent to the given node. This optimization produces a local community that contains all the nodes for which the greatest difference exists between the nodes in the local community and those outside the local community, resulting in a first iteration community, C1.

The algorithm then proceeds to a second node and repeats the procedure, adding members or removing nodes to C1, while optimizing the proportion of internal and external edges. Ultimately, this method produces Cn, which is interpreted as a community within that network. This method can also be used to identify multiple, overlapping communities in a given network. This method, which has been used in identifying communities in online networks (i.e., the World Wide Web or cell phone communication networks), serves as the basis for our approach to identifying collectives in online teacher professional development.

Documenting Collective Development of Online Communities

This section  provides an overview for a proposed method for documenting the collective development in an online community. The method builds on the research methods for studying collective development in a face-to-face setting, but has been adapted to meet the unique challenges and readily available data generated in online contexts. The method involves the following four phases:

1. Generate interactional data. Interactional data are often generated by learning management systems but are sometimes difficult to collect in a usable form. Operationally, we generate a spreadsheet that includes a row for each post. Each post is identified by forum (discussion), thread, the author, the recipient, the content of the post, and the date and time the post was made.
2. Identify cohesive subgroups using cluster analysis. Initial analysis of the interactional data is conducted using software specifically designed to identify clusters (subgroups) within the group using the methods already described.  We use Meerkat, a social network analysis tool (http://aicml.cs.ualberta.ca/?q=node/41) to conduct our initial analysis and to identify particularly cohesive collectives. We claim that these cohesive collectives are the intermediate grain size most appropriate for focusing on collective development and accomplishments in an online setting; when any larger group is used, no evidence indicates a collective exists about which to make claims.
3. Delineate which threads/utterances can be used to make claims about collective development and accomplishment. This phase involves identifying the specific threads (groupings of posts with a specific theme and with defined participants) that can be used as data for claims about collective development and accomplishments.  Specifically, for each thread, we calculate a viability index for each cohesive collective identified in Phase 2. This viability index is the ratio of the posts in the thread generated by members of the collective to total posts in the thread. If the viability index is greater than 80%, we describe the thread as viable.
4. Develop and test conjectures about collective development and accomplishments. The final phase involves using face-to-face methods (Dean, 2005; Rasmussen & Stephan, 2008) to test and revise conjectures about collective development and accomplishments. This method is a consistent with Glaser and Strauss’ (1967) constant comparative method.  The distinguishing feature of their method is that as new utterances are analyzed, they are compared with currently conjectured themes or categories.  This process of constantly comparing utterances leads to the ongoing refinement of the theoretical categories that remain grounded in the data.  As Glaser and Strauss noted, negative cases that appear to contradict a current category are of particular interest and are used to further refine the emerging categories.

In contrast to typical analysis of online interaction, where the whole group or arbitrary subgroups are the unit of analysis, the unit of analysis in our method is an empirically identified cohesive collective. Similarly, while all posts are coded and used so we can better understand the students and the course, posts to viable threads—as opposed to posts in general— are the data against which conjectures about normative ways of reasoning with in a collective are tested and revised.

Use Case: Discussion Boards in an Online Class

One online class was analyzed to illustrate both the method and the potential implications of collective analysis of online classes. The specific sections of this online mathematics content course for teachers included 497 interactions between 24 participants. The overall instructional goal for this course was to support teachers in developing particular mathematical insights, understandings, and skills needed to teach algebra from a functions-based perspective (Chazan, 2000) through analysis and extension of tasks and concepts from the school mathematics curriculum.

The course was fully online and conducted using the BlackBoard Learning management system. Our analysis should not be considered a complete analysis of this class. Rather, it is provided to further illustrate the collective analysis method and to highlight the potential utility for the analysis.

Phase 1

This phase of analysis remained fairly primitive. In order to generate the necessary information in a usable format, we copied the fully expanded discussion board in plain text format and manually parsed this data into six columns: forum, thread, date/time, from, to, and content. Automating this process may be fairly straightforward, but we have not had the time or funds to explore this development.

Phase 2

A variety of tools and software packages are available to implement SNA and cluster analysis. We used Meerkat to automate the process of conducting iterative local expansion to identify cohesive collectives. Meerkat used SNA techniques to categorize the participants (nodes) into three groups. Two cohesive collectives are depicted as pink and orange nodes in Figure 1, as well as those who were not members of a cohesive collective (these “No Community” members are depicted as blue nodes). These two cohesive collectives each had higher interactions (both to and from) with other members of the collective than with members outside the collective.

Figure 1. Cohesive cllective identification.

Analysis of the smaller collective revealed that although there were higher within-collective interactions than outside-collective interactions, the analysis was limited by the fact that it focused on optimizing ratios, producing a collective with high cohesion but with only a total of 11 edges (interactions) between them. Thus, we considered those participants also part of the No Community group (blue).

This analysis provided us with a necessary first step for analysis of the emergence of normative practices in our online work. By definition, membership in C1 (nodes colored pink) indicates a large number of interactions between members of the collective. We cannot assume that each member of C1 had carefully read and reflected on each utterance from the 3 weeks, but the high cohesion of the group indicates that they likely had participated (either actively through posting or passively through reading) in much of the discussion. In other words, their participation was likely, much like those in a face-to-face conversation: They were in the room, so to speak, and more likely than not paying attention, but their focus may have been elsewhere at times.

Those participants who were members of the No Community group (blue) also had a large number of posts, but their posts were more broadly dispersed, indicating that these individuals were neither a major channel of information for their colleagues nor an individual that others sought out. In other words, these individuals’ contributions were unlikely used by their colleagues and their colleagues’ contributions did not likely influence them.

Phase 3

With the preliminary analysis in place, we were able to begin analysis of collective development, focusing on studying the collective development and achievement of C1. Members of this group were likely to have participated (either actively through posting or passively through reading) in much of the discussion. In contrast, the outsiders or peripheral participants were unlikely to have been a major channel of information for their colleagues nor an individual that others sought out. Further, this group’s contributions were unlikely to have been used by their colleagues in C1 and the contributions of their colleagues’ in C1 were unlikely to have influenced them.

While the contributions of those outside C1 are important and can have theoretical significance for particular research questions, we posited that the contributions of these students could not be used as evidence of collective development, particularly the collective development of C1. That being said, given the dynamic nature of social interactions, a reciprocal relationship existed between members of C1 and those outside the collective (C1′), and the contributions of members of C1′ were of potential importance.

First, once collectives are established, and (ideally, desirable and generative) norms and mathematical practices are documented, the instructor’s role is to support members of C1′ inculcation into these norms and practices. Additionally, noting that collectives are dynamic and morph over time, documenting individuals transition from outside the collective to inside the collective and fine grained analysis of the conditions that supported that transition are potentially fruitful from both a research and instructional perspective.

Given this initial analysis, we returned to the online interactions (discussion board) and identified threads where contributions from C1 represented significant proportions of the interactions. Figure 2 visually depicts the result of analysis of the viability of each thread in Weeks 3, 4, and 5. Specifically, each thread (represented by week_thread number), is identified as green or red. Green threads are those where more than 80% of the posts were from the collective (viable threads), while red threads represent those where less than 80% of the posts were from the collective. The decimal form of the viability index is displayed next to each colored circle.

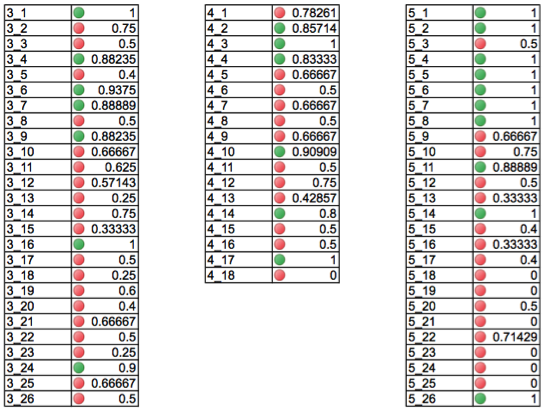Figure 2. Viability index table.

This viability index table delineates the threads to be used as data to develop, test, and refine conjectures regarding the collective development of the cohesive collection in question.

Phase 4

During Phase 4, our analysis was similar to Dean’s (2005) and Rasmussen and Stephan’s (2008) method for documenting collective activity using the constant comparative paradigm, with the exception that we had to restrict the data to focus only on those threads that were considered viable. Continuing the previous example, open coding of the entire data set resulted in four primary themes across the data set: talking trigonometry, providing qualitative descriptions of the characteristics of graphs, and grounding explanations and solutions in the quantities and context of the problem (speaking with meaning). A query matrix was then compiled, organizing all posts by both the theme and the viability index of the thread. This query matrix is shown in Table 1.

Table 1
Query Matrix by Theme and Viability

This query matrix allowed us to focus our attention when exploring collective characteristics. More specifically, as the table was generated by NVivo9 data analysis software, it allowed us to generate reports that focused specifically on the viable posts in each category. While we did not have enough data to present empirically verified conjectures, preliminary analysis allowed us to develop a number of conjectures about collective activity: language and ideas that have become established within this collective through patterns of interaction (Rasmussen & Stephan, 2008).

These conjectures are presented as examples of collective reasoning, but we need to conduct further analysis to determine whether these conjectures are valid beyond the small data set analyzed in this example. They highlight the potential utility of this analysis, both from an instructional and a research perspective.

Talking Trigonometry. The first emerging normative way of reasoning about the mathematics within this collective involved using standard trigonometry terms and language to describe particular tasks and activity. Specifically, participants regularly referred to key aspects of right triangle trigonometry, including the definition of the sine as “opposite over hypotenuse” and the pneumonic device “SOHCAHTOA” to remember the relationship between sides and specific trigonometric ratios. Additionally, teachers described and performed the standard procedure to find the period of a trigonometric function given its algebraic representation; that is, the period of sin(nx) is 2π/n.

Describing Graphs Qualitatively. The second emerging normative way of reasoning about the mathematics was describing the qualitative features of trigonometric graphs. For example, the teachers commonly described the graph of y = sin(x) as “wavy.” They also accepted describing the maximum and minimum values of the range of the function and talking about how the function repeated itself. In each of these cases, it appeared that the graph was taken as evidence of the claim.

Speaking With Meaning. A third emerging normative way of reasoning about the mathematics within this collective was the notion of speaking with meaning, which Clark, Moore, and Carlson (2008) described as discourse where “responses are conceptually based, conclusions are supported by a mathematical argument, and explanations include reference to the quantities in the problem context” (p. 298).

Specific examples of the theme Speaking With Meaning included an emphasis on describing angles as measurable quantities, including how they are measured and the meanings of units of angular measure. Additionally, explanations of functions and graphs focused on quantities and relationships and moved beyond the qualitative features of the graph. For example, the teachers noted that the graph of y = sin(x) has a maximum of 1, because as the angle varies the opposite side of a right triangle embedded within a unit circle cannot get any larger than the radius of the unit circle.

Discussion

The illustrative case and preliminary analysis in this paper highlights the potential of this method. Results such as those delineated here can serve as both summative and formative assessment for instructors. First, the results shed light on the norms and collective understandings emerging in specific collectives and provide an additional metric for documenting mathematical development. Additionally, results can provide instructors with formative guidance. For example, in the case of the emergence of norms and mathematical practices that are particularly productive and useful—such as Speaking With Meaning—within specific collectives, it may be useful to purposefully organize students into heterogenous groupings that include some students for whom the practice is normative and some for whom it is not. In this way, members of the collective can serve as brokers (Lave & Wenger, 1991), introducing the norms and practices from their collective to a new group.

A relationship appeared to exist between the week-by-week course foci and the collective mathematical reasoning. For example, trigonometry was introduced in Week 3 and was the focus of Weeks 4 and 5. The overlay of the weekly focus on to the results leads to a variety of conjectures and topics for further research. For example, in Figure 3, the number of utterances falling into the category Talking Trigonometry decreased from Week 3 to 5 for the identified cohesive collective. This result may indicate some transition in the focus of the collective, and additional analysis could explore both how other collective understandings, such as Speaking with Meaning, emerged alongside Talking Trigonometry. When, if ever, Talking Trigonometry ceased to be a collectively held focus of activity for the collective could also be explored.

Figure 3. Summary of the category Talking Trigonometry.

Evidence indicated that the category Talking Trigonometry emerged for threads generated by individuals outside the collective. Of particular significance would be detailed analyses that explore the relationships between this emergence and (a) the course curriculum and (b) participation alongside members of the collective. Specifically, this analysis could indicate that outsiders to the collective had begun to adopt the collective practices of the collective, and additional analysis of the potential benefits of peripheral participation (Lave & Wenger, 1991) could provide interesting characterizations of this phenomenon.

Conclusion

Collective learning is a significant focus in research and development in mathematics teacher professional development. As online teacher professional development grows, the need for online communities to support teachers as they attempt to maintain and adapt high-leverage professional practices will also increase. However, professional communities—and not just informal groupings of teachers—are clearly important to nurture and sustain generative growth (Franke et al., 2001; Nelson & Hammerman, 1996; Wilson & Berne, 1999). Grossman et al. (2001) argued for the importance of distinguishing between a community of teachers and a group of teachers:

Even a cursory review of the literature reveals the tendency to bring community into being by linguistic fiat.  Groups of people become communities, or so it would seem, by the flourish of a researcher’s pen.  Researchers have yet to formulate criteria that would allow them to distinguish between a community of teachers and a group of teachers sitting in a room for a meeting. (p. 943)

Although much progress has been made in documenting professional communities and collective practices in face-to-face settings, little analogous research exists for online community development. In this paper, we proposed a method that we have found useful in documenting the development of online communities. This method builds on existing methodologies, but adds additional steps needed to address characteristics of interaction that are unique to the online setting.

The methods discussed in this paper hold much potential for both research and practice. Specifically, research on online collectives can assist in identifying the emergence of collective ways of reasoning about mathematics, as well as for identifying shifts in groups for whom these collective ways of reasoning are normative—two aspects of learning that are not easily identified by instructors in the moment. This information, in turn, can provide instructors with instructional suggestions, such as specific groupings of students or instructional foci. Further exploration of this method in practice and discussions of successes or modifications needed for broader use are needed and encouraged.

References

Achinstein, B. (2002). Community, diversity, and conflict among schoolteachers. New York, NY: Teachers College Press.

Chazan, D. C. (2000). Beyond formulas in mathematics and teaching. New York, NY: Teachers College Press.

Chen, J., Zaïane, O. R., & Goebel, R. (2009, June). Detecting communities in large networks by iterative local expansion. Paper presented at the International Conference on Computational Social Networks, Fountainbleau, France.

Clark, P. G., Moore, K. C., & Carlson, M. P. (2008). Documenting the emergence of “speaking with meaning” as a sociomathematical norm in professional learning community discourse. The Journal of Mathematical Behavior, 27(4), 297-310. doi: 10.1016/j.jmathb.2009.01.001

Cobb, P., Stephan, M., McClain, K., & Gravemeijer, K. (2001). Participating in classroom mathematical practices. Journal of the Learning Sciences, 10, 113-164.

Cobb, P., Zhao, Q., & Dean, C. (2009). Conducting design experiments to support teachers’ learning: A reflection from the field. Journal of the Learning Sciences, 18(2), 165-199.

Dean, C. O. (2005). An analysis of the emergence and concurrent learning of a professional teaching community (Unpublished doctoral dissertation). Department of Teaching and Learning, Vanderbilt University, Nashville, TN.

Franke, M. L., Carpenter, T. P., Levi, L., & Fennema, E. (2001). Capturing teachers’ generative change: A follow-up study of teachers’ professional development in mathematics. American Educational Research Journal, 38, 653-689.

Franke, M. L., & Kazemi, E. (2001). Teaching as learning within a community of practice: Characterizing generative growth. In T. Wood, B. S. Nelson & J. Warfield (Eds.), Beyond classical pedagogy in elementary mathematics: The nature of facilitative teaching (pp. 47-74). Mawah, NJ: Lawrence Erlbaum Associates.

Gamoran, A., Anderson, C., Quiroz, P., Secada, W., Williams, T., & Ashman, S. (2003). Transforming teaching in math and science: How schools and districts can support change. New York, NY: Teachers College Press.

Glaser, B., & Strauss, A. (1967). The discovery of grounded theory:  Strategies for qualitative research. Chicago, IL: Aldine Publishing Company.

Grossman, P. L., Wineburg, S. S., & Woolworth, S. (2000, April). In pursuit of teacher community. Paper presented at the at the American Educational Research Association, New Orleans, LA.

Grossman, P. L., Wineburg, S. S., & Woolworth, S. (2001). Toward a theory of teacher community. The Teachers College Record, 103(6), 942-1012.

Kazemi, E., & Franke, M. L. (2004). Teacher learning in mathematics: Using student work to promote collective inquiry. Journal of Mathematics Teacher Education, 7, 203-225.

Lave, J., & Wenger, E. (1991). Situated learning: Legitamate peripheral participation. New York, NY: Cambridge University Press.

Lehrer, R., & Schauble, L. (1998, April). Developing a community of practice for reform of mathematics and science. Paper presented at the annual meeting of the American Educational Research Association, San Diego, CA.

Little, J. W. (2002). Locating learning in teachers’ communities of practice: Opening up problems of analysis in records of everyday work. Teaching and Teacher Education, 18, 917-946.

National Council of Teachers of Mathematics. (2014). Principles to action. Reston, VA: Author.

Nelson, B. C., & Hammerman, J. K. (1996). Reconceptualizing teaching: Moving toward the creation of intellectual communities of students, teachers, and teacher educators. In M. W. McLaughlin & I. Oberman (Eds.), Teacher learning: New policies, new practices (pp. 3-21). New York, NY: Teachers College Press.

Newmann, F. M., & Associates. (1996). Authentic achievement: Restructuring schools for intellectual quality. San Francisco, CA: Jossey-Bass.

Nickerson, S. D., & Moriarty, G. (2005). Professional communities in the context of teacher’ professional lives: A case of mathematics specialists. Journal of Mathematics Teacher Education, 8, 113-140.

Penuel, W. R., & Riel, M. (2007). The ‘new’ science of networks and the challenge of school change. Phi Delta Kappan, 88(8), 611-615.

Penuel, W. R., Sussex, W., Korbak, C., & Hoadley, C. (2006). Investigating the potential of using social network analysis in educational evaluation. American Journal of Evaluation, 27(4), 437-451. doi: 10.1177/1098214006294307

Rasmussen, C. L., & Stephan, M. (2008). A methodology for documenting collective activity. In A. E. Kelly, R. A. Lesh & J. Y. Baek (Eds.), Handbook for innovative design research in science, technology, engineering, and mathematics (STEM) education (pp. 195-215). New York, NY: Taylor & Francis.

Rogoff, B. (1994). Developing understanding of the idea of communities of learners. Mind, Culture, and Activity, 1, 209-229.

Rogoff, B. (1995). Observing sociocultural activity on planes: participatory appropriation, guided participation, and apprenticeship. In J. V. Wertsch & A. Alvarez (Eds.), Sociocultural studies of the mind (pp. 139-164). New York, NY: Cambridge University Press.

Rosebery, A., & Warren, B. (1998, April). Re-examining change in teacher professional development. Paper presented at the annual meeting of the American Educational Research Association, San Diego, CA.

Secada, W. G., & Adajian, L. B. (1997). Mathematics teachers’ change in the context of their professional teaching communities. In E. Fennema & B. S. Nelson (Eds.), Mathematics teachers in transition (pp. 193-219). Mawah, NJ: Lawrence Erlbaum Associates.

Sfard, A. (2000). On reform movement and the limits of mathematical discourse. Mathematical Thinking and Learning, 2(3), 157-189.

Smith, G., & Ferguson, D. (2002). Teaching over the Web versus in the classroom: Differences in instructor experience. International Journal of Instructional Media, 29(1), 61-67.

Stein, M. K., & Brown, C. A. (1997). Teacher learning in a social context: Integrating collaborative and institutional processes with the study of teacher change. In E. Fennema & B. Scott Nelson (Eds.), Mathematics teachers in transition (pp. 155-192). Mahwah, NJ: Erlbaum.

Stein, M. K., Silver, E. A., & Smith, M. S. (1998). Mathematics reform and teacher development: A community of practice perspective. In J. G. Greeno & S. V. Goldman (Eds.), Thinking practices in mathematics and science learning (pp. 17-52). Mahwah, NJ: Lawrence Erlbaum Associates.

Su, B., Bonk, C. J., Magjuka, R., J., Liu, X., & Lee, S.-h. (2005). The importance of interaction in web-based education: A program-level case study of online MBA courses. Journal of Interactive Online Learning, 4(1), 1-19.

Toulmin, S. (1969). The uses of argument. Cambridge, UK: Cambridge University Press.

Voigt, J. (1995). Thematic patterns of interaction and sociomathematical norms. In P. Cobb & H. Bauersfeld (Eds.), The emergence of mathematical meaning : interaction in classroom cultures (pp. 163-201). Hillsdale, NJ: L. Erlbaum Associates.

Warren, B., & Rosebery, A. (1995). Equity in the future tense: Redefining relationships among teachers, students, and science linguistic minority classrooms. In W. Secada, E. Fennema & L. Byrd (Eds.), New directions in equity for mathematics education (pp. 298-328). New York, NY: Cambridge University Press.

Wasserman, S., & Faust, K. (1994). Social network analysis: Methods and applications. New York, NY: Cambridge University Press.

Wenger, E. (1998). Communities of practice: Learning, meaning, and identity. New York, NY: Cambridge University Press.

Westheimer, J. (1998). Among school teachers: Community, autonomy, and ideology in teachers’ work. New York, NY: Teachers College Press.

Wilson, S. M., & Berne, J. (1999). Teacher learning and the acquisition of professional knowledge: An examination of research on contemporary professional development. In A. Iran-Nejad & P. D. Pearson (Eds.), Review of research in education (Vol. 24, pp. 173-209). Washington, DC: American Educational Research Association.

Wojnar, L. (2002). Research summary of a best practice model of onlnie teaching and learning. English Leadership Quarterly, 25(1), 2-9.

Author Notes

This material is based upon work supported by the National Science Foundation under grant number DRL-1222355.

Chrystal Dean
Appalachian State University
Email: [email protected]

Jason Silverman
Drexel University
Email: [email protected]