Research on the use of instructional technology in secondary mathematics education has proliferated over the last 20 years (e.g., Burrill et al., 2002; Heid & Blume, 2008; Zbiek, Heid, Blume, & Dick, 2007) and has demonstrated that the strategic use of technological tools such as graphing calculators, dynamic geometry software (DGS), and spreadsheets can deepen students’ mathematical content knowledge and support students’ mathematical thinking and discourse.
At the same time, awareness and interest in students’ mathematical thinking, reasoning, and sense-making has increased (Boaler & Staples, 2008; Cuoco, Goldenberg, & Mark, 1996; Hollebrands, Conner, & Smith, 2010; National Council of Teachers of Mathematics [NCTM], 2000, 2009; Romberg, 1994; Stein, Smith, Henningsen, & Silver, 2009; Suh, 2010). These sorts of behaviors have been articulated and promoted in NCTM’s (2000) Process Standards, but have received greater attention recently due to their inclusion of the Standards for Mathematical Practice in the Common Core State Standards (Common Core State Standards Initiative, 2010), adopted by a majority of states in the U.S. However, little research has focused on how the use of technology can support students’ mathematical thinking and reasoning.
The purpose of this study was to investigate how middle and secondary mathematics teachers use technology for instruction, especially as it relates to students’ opportunities to engage in higher level mathematical thinking. The Mathematical Tasks Framework (Stein & Smith, 1998) was used to assess the cognitive demand of mathematical tasks implemented in four mathematics classrooms and to investigate the role of technology in both low- and high-level cognitive demand tasks.
Evidence indicates that, while these teachers used technology in a way that was generally consistent with their practice in terms of the cognitive demand of the tasks, the use of technology as a reorganizer was strongly correlated with these teachers’ attempts to engage their students in high-level mathematical thinking. These general trends are delineated among four teachers, and specific classroom examples are used to describe and develop the role of technology as an amplifier or a reorganizer at the task level.
Theoretical Background
This section discusses the theoretical frameworks used to characterize students’ mathematical thinking and their use of technology. The Mathematical Tasks Framework (Stein & Smith, 1998), a taxonomy for evaluating the mathematical thinking requirements of a task during various phases of classroom enactment, was used to characterize students’ mathematical thinking, while the metaphors of amplifier and reorganizer (Pea, 1985, 1987) were used to describe the use of technological tools.
The Mathematical Tasks Framework
Whether technology is used or not, teachers shape students’ mathematical learning and view of the discipline of mathematics by the choice of mathematical tasks for instruction (NCTM, 1991). The Mathematical Tasks Framework (Stein & Smith, 1998) describes and differentiates the type of thinking that is called for by a given mathematical task, defined as “a classroom activity, the purpose of which is to focus students’ attention on a particular mathematical idea” (Stein, Grover, & Henningsen, 1996, p. 460).
This framework distinguishes between low-level cognitive demand tasks, including memorization and the use of procedures without connections to meaning or concepts, and high-level cognitive demand tasks, including the use of procedures with connections to meaning or concepts, and doing mathematics, of which nonalgorithmic thinking is characteristic. The Task Analysis Guide (Stein et al., 2009; Stein & Smith, 1998) described these four categories in greater detail. An important characteristic of this framework is that it is not tied to specific mathematical content, but rather characterizes different types of thinking in which students may engage while working on a range of mathematical tasks across a variety of mathematical domains. The aim of this study was to investigate and describe the opportunities for thinking specifically related to the use of technological tools.
Beyond the distinctions with respect to the types of thinking called for by a mathematical task, the Mathematical Tasks Framework makes an important connection to classroom practice by acknowledging that the thinking requirements of a task may change during its enactment. The task as it appears in curricular materials does not directly influence students’ learning by the type of thinking it requires. Those demands may be altered by the teacher when introducing the task to students during instruction, known as the set-up phase, and again while students are working on the task, referred to as the implementation phase. This element of the Mathematical Tasks Framework makes it especially suitable for describing students’ thinking in a classroom context.
Research has shown that the type of tasks that students engage with and the type of thinking that students do while engaging with those tasks have important implications for students’ learning (Boaler & Staples, 2008; Huntley, Rasmussen, Villarubi, Sangtong, & Fey, 2000; Stein et al., 1996; Stein & Lane, 1996). In general, students who have engaged with higher level mathematical tasks have demonstrated a greater ability to employ multiple solutions strategies, utilize multiple and connected representations, use graphing calculators to solve problems, and explain their reasoning than do those who have not.
The greatest gains have been associated with students who engaged with tasks at a high level during the implementation phase. However, there is evidence that students benefit from being exposed to high-level tasks during the set-up phase, even if the thinking requirements decline during implementation, over those students who consistently work on low-level tasks (Stein & Lane, 1996).
In sum, the choice of mathematical tasks has important implications for students’ understanding of the discipline of mathematics and for the quality of their mathematical thinking and learning. Thus, it is important to understand the role that technology might play in relation to the tasks that teachers choose to enact with their students.
Digital Cognitive Technologies
Digital technologies have become ubiquitous in secondary school settings and can serve a variety of purposes within mathematics classrooms. Peressini and Knuth (2005) identified five ways that digital technologies can serve as a tool for teachers in the mathematics classroom: as a tool for management, communication, evaluation, and motivation and as a cognitive tool (see Figure 1). The interest in this study is with digital technologies used specifically as cognitive tools, or “cognitive technologies” (Pea, 1985, 1987).
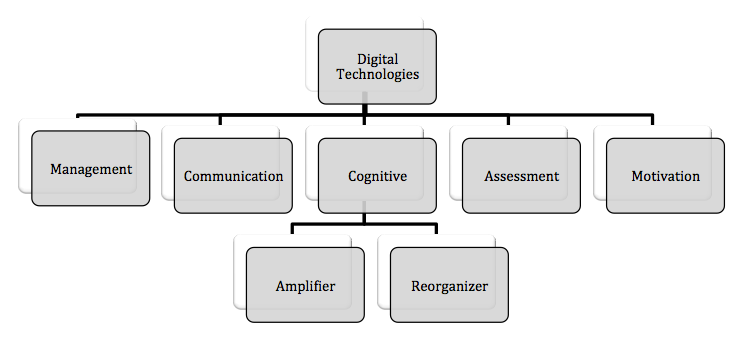 Figure 1. Amplifier and reorganizer as digital cognitive technologies.
Figure 1. Amplifier and reorganizer as digital cognitive technologies.
Pea (1987) defined cognitive technologies as those that “help transcend the limitations of the mind (e.g., attention to goals, short-term memory span) in thinking, learning, and problem-solving activities” (p. 91). By mediating human thought, cognitive technologies both assist and influence thought and learning. Although cognitive technologies are not limited to digital technologies (e.g., written language, abstract mathematical notation, chalkboards), the discussion in this article is limited to digital cognitive technologies that may serve as a medium for mathematical activity. Combining the use of presentation software and a computer projector for displaying geometric figures would be an example of a digital cognitive technology, while the use of a blackboard for the same purpose would be an example of a cognitive technology that is not digital. Only digital cognitive technologies were under consideration in this study.
Amplifier and Reorganizer Metaphors
A further distinction within cognitive technologies is between their use as an amplifier or a reorganizer of mental activity (Pea, 1985, 1987). When technology is used as an amplifier, it performs more efficiently tedious processes that might be done by hand, such as computations or the generation of standard mathematical representations. In this use of technology, what students do or think about is not changed but can be accomplished with significantly less time and effort and more accuracy. The use of a scientific calculator for computations while students set up and solve proportions can make their work more efficient and help to avoid basic arithmetic errors in their solutions. However, students’ activity and thinking is generally unchanged by this use of the calculator, as their cognitive focus is still on setting up and solving proportions whether the calculator is used or not.
As a reorganizer, technology has the power to affect or shift the focus of students’ mathematical thinking or activity. Some examples include producing novel representations, which make salient some aspect of a concept that is difficult to make explicit without it, or by providing feedback to students to which they would otherwise not have access. Students might use DGS to construct a triangle and its medians in order to look for patterns and make and test conjectures about the relationships between the medians of a triangle (i.e., they intersect at a single point called the centroid or the centroid divides each median into two segments whose lengths have a constant ratio of 2).
By using technological tools to generate and measure dynamic and interactive representations, students are able to focus on looking for patterns and making and testing conjectures rather than on drawing and measuring triangles. This use of technology supports a shift in the focus of students’ mathematical activity and thinking from drawing and measuring to looking for patterns and making and testing conjectures.
Pea’s original distinction was made around the advent of personal computers in educational contexts and was not specifically mathematical. However, the question he raised with this distinction was a fundamental one that persists in education today: Will technology be used to support a fundamental shift in how students think and interact with the curriculum, or will it simply add bells and whistles to the status quo?
This question is one that has been taken up in mathemathics education in a number of contexts, and the idea of using cognitive technologies as amplifier or reorganizer has been developed and applied in number of ways. It has been used to describe and organize the literature on the use of technology in mathematics education (Heid, 1997; Zbiek et al., 2007) and has been used by researchers in describing uses of technology in mathematical instruction and learning (Ben-Zvi, 2000; Goos, Galbraith, Renshaw, & Geiger, 2003; Lee & Hollebrands, 2008; Zbiek et al., 2007). The purpose of this paper is to develop this distinction further at the level of a mathematical task and connect it to students’ mathematical thinking, so that it might guide instruction and teacher education.
This distinction applies to two contexts that are not intended by this study: that of reorganizing the curricular sequence of a course and that of reorganizing the structure of the learning environment. In the former case, the use of technology as a reorganizer has been used to describe how the structure of the content of a course or curricular unit was changed to emphasize concepts or ideas different from the status quo.
The use of technology allows for the K-12 curriculum to be reorganized, giving priority to a different set of skills and abilities than what has traditionally been the goal of mathematics education. There are numerous cases in the literature of using technology as a reorganizer to restructure the curricular content of mathematics courses (e.g., Chazan, 1999, 2000; Heid, 1988; Judson, 1990; O’Callaghan, 1998; Palmiter, 1991; Schwarz & Hershkowitz, 1999).
Another way in which technology can be a reorganizer is in terms of the structure of the learning environment. The flipped model of instruction is becoming increasingly popular in a number of disciplines at the secondary and post-secondary level, including mathematics (Boutell & Clifton, 2011; Deslauriers, Schelew, & Wieman, 2011; Foertsch, Moses, Strikwerda, & Litzkow, 2002; Gannod, Burge, & Helmick, 2008; Lage, Platt, & Treglia, 2000; Moore, Gillett, & Steele, 2014; Novak, Patterson, Gavrin, Christian, & Forinash, 1999; Prober & Heath, 2012; Strayer, 2012; Winterbottom, 2007).
In general, the flipped model of instruction utilizes technology by having students view video lectures outside of class in order to spend class time engaging students in working on problems or projects or discussing problems or issues in small or large groups. In this way, the use of technology has allowed the structure of instruction to be reorganized so that the mode of instruction traditionally used in class (such as lecture) can now be conducted outside of class, while activities traditionally taking place outside of class (such as completing problems or projects) can take place during class.
Although technology can play a role in reorganizing the curriculum or the structure of the learning environment, the current use of the amplifier and reorganizer metaphor is at the mathematical task level, describing how the use of technology can influence what students do and how they think mathematically. For example, Doerr and Zangor’s (2000) description of the use of the graphing calculator as a transformational tool seems to align with the idea of a reorganizer at the task level. Specifically, they cite the use of the graphing calculator “whereby tedious computational tasks were transformed into interpretive tasks” (p. 152-3). The teacher in their study required students to interpret the results of data analysis and modeling in terms of the context of the problem by offloading computations such as the calculation of regression equations from numerical data.
Goos et al. (2003) discussed four roles that technology can play for students in the mathematics classroom: master, servant, partner, and extension of self. They aligned the servant role with the use of technology as amplifier, performing tedious or menial tasks of computation or representation, while as a partner or extension of self technology acts as a reorganizer of students’ mathematical thinking and activity.
In his discussion of using technological tools in the learning of data analysis, Ben-Zvi (2000) used the amplifier-reorganizer distinction to discuss the ways in which students’ activity and thinking may be reorganized by the use of these tools. In particular, he claimed that the use of technological tools can reorganize students’ work by shifting their activity to a higher cognitive level, changing the objects of the activity, and focusing the activity on transforming and analyzing representations. These sorts of behaviors are examples of how the purpose or focus of a mathematical task can be reorganized by the inclusion of technology.
An important aspect of the type of thinking afforded by the use of technology is the kind of task that calls for its use. The inclusion of technology requires an understanding of the kinds of tasks that may utilize the resources provided by the technology to support students’ high-level thinking. “Some researchers also suggest that the choice of the task in relation to the affordances of the dynamical geometry environment may be critical for the development of the understandings of the students” (Hollebrands, Laborde, & StraBer, 2008, p. 174). Thus, an aim of this study was to explicate better the role of technology within the tasks in which it was used. The amplifier and reorganizer metaphors for technology use provide a way to describe how students’ thinking might be influenced by the inclusion of technology.
In this study, the amplifier-reorganizer distinction is used to describe the role of technology in relation to the cognitive demand of mathematical tasks with which students engage. One adaptation that was made to the amplifier and reorganizer metaphors during a pilot study was the inclusion of the possibilities of technology being used as both an amplifier and a reorganizer. When technology is used as both an amplifier and a reorganizer, the purpose of making tedious computations or generation of standard mathematical representations more efficient and accurate by automating them is to support a shift in students’ focus to some other aspect of the task.
For example, using DGS to construct a triangle and measure the interior angles and side lengths is considered an amplifier use of technology. This procedure can be done using paper, pencil, a ruler, and a protractor. Even dragging the vertices of the triangle to reshape it is a more efficient way of creating numerous triangles. However, when students are asked to construct and measure triangles using a DGS to investigate the sum of the interior angles of a triangle, then DGS is intended to be used as a reorganizer as well, since the purpose of creating and measuring triangles is to observe relationships and to make and test conjectures about the properties of triangles.
The use of technology as an amplifier in this case has the potential to support a shift in students’ focus and behavior and the purpose of the task by offloading the construction and measurement of mathematically precise triangles to the technological tools. In this way, the reorganizer use of technology depends upon its use as an amplifier as a sort of necessary condition.
Thus, the research questions that this study sought to answer are the following:
- How is the use of technology related to the cognitive demand of mathematical tasks as set up and implemented?
- What is the role of technology in low-level tasks?
- What is the role of technology in high-level tasks?
Research Methods
The study was observational in nature. There was no attempt to design or influence mathematics instruction in these classrooms, but rather to observe how teachers used technology for instruction and how that use was related to students’ opportunities to engage in mathematical thinking. The study employed a mixed methods research design with the goal of understanding how classroom teachers use technology to support the mathematical thinking of their students. Although the data collected were qualitative in nature, codes for students’ thinking and technology use during the various stages of implementation were collected and counted in order to reveal general patterns and associations. Thus, the data analysis included a quantitative element.
The Setting
Four teachers were recruited primarily based on the fact that they used technology for mathematics instruction. Each teacher designated one or two units of instruction that were observed in each classroom over a period of 4 to 6 weeks. Each of the teachers had 3 years of teaching experience and had taught the observed unit at least once previously. A geometry unit was observed in each of the three secondary classrooms, and two units were observed in the same middle school classroom, one on the order of operations and another introducing operations with fractions.
Because the research questions posed for this study did not relate to a particular cognitive technology but rather to ways a given technology was used, a variety of technologies were observed in these teachers’ classrooms, including scientific and graphing calculators, interactive whiteboards (IWBs), and DGS. The technologies that teachers chose to use are part of the answer to the question regarding how technology was used.
In general, IWBs were used by the teacher, and DGS and calculators were used by students. On a few occasions, the teacher used DGS with their computer screen projected for a demonstration. In a few others, students were invited to the front of the class to manipulate the IWB. An overview of the data collection classrooms is given in Table 1.
Table 1
Summary of Data Collection Classrooms
Teachers [a] | Tasks Observed | Grade/Class Level | Topics | Technologies |
| Ms. Jones | 12 | 9th-grade Integrated Math |
|
|
| Ms. Young | 17 | 11th-grade Inclusion |
|
|
| Mr. Mack | 17 | 6th-grade Regular |
|
|
| Ms. Lowe | 17 | 10th-grade Advanced |
|
|
| [a] All names are pseudonyms | ||||
Data Collection and Coding
Data collected at each site included lesson observation field notes, task artifacts, student work on the task, and audio recorded postlesson interviews with the teacher, which were subsequently transcribed. Following Stein et al. (1996), a mathematical task was defined as “a classroom activity, the purpose of which is to focus students’ attention on a particular mathematical idea” (p. 460). Students might engage in more than one task in a given lesson, and in practice the introduction of a new mathematical topic or activity was used to demarcate tasks.
The Task Analysis Guide (Stein & Smith, 1998) was used to code each task with respect to whether the cognitive demand of the task was high or low during two of the three phases of enactment: tasks as set up by the teacher prior to students working on the task and as implemented in the classroom as students engaged with the task.
The question guiding the coding of tasks during the implementation phase was, “What type of thinking do the majority of students seem to be engaged in for a majority of the task?” Students’ interactions with each other, the teacher, and the technology (when used), as captured in lesson observation field notes and the work that students produced on the task were the evidence used in answering this question. Thus, these qualitative data were compiled to create a detailed representation of the lesson that was used to assess the type of thinking in which most students engaged and the ways technology was used.
To ensure that these representations were valid, two reliability coders were used throughout the data collection process. One coder accompanied the researcher to the classroom and coded the task directly from the observation of the implementation and the collected student work, while the second coder coded the task from the lesson observation field notes, task artifacts, and student work. Coders alternated roles so that each coded approximately half of the tasks from observations and half from the lesson observation field notes.
Approximately one fourth (24%) of the observed tasks were coded for reliability. Agreement on the cognitive demand was 98% with the lesson observer and 83% with the field note coder. All discrepancies were resolved, and the consensus code was assigned to the task.
In addition, for those tasks that utilized technology as a cognitive tool, the use of technology was coded as amplifier, reorganizer, or both during the set-up and implementation phases. Technology use during the set-up phase refers to the way in which technology was intended to be used in the task as set up by the teacher, but prior to students actually engaging with the task. For example, if the teacher introduced a task in which students were to use DGS to investigate the properties of medians of a triangle, the use of technology was coded as an amplifier and reorganizer during set up.
Technology use during the implementation phase was based on what actions students performed with the technology and how those actions related to their work on the task. For example, if students created and dragged figures, but did not use those actions to generate conjectures, then the use of technology was coded as amplifier. DGS made the actions students performed more efficient and accurate, but did not result in students shifting their focus to looking for patterns or making generalizations.
Agreement on technology use was 86% with the lesson observer and 86% with the field note coder as well. All discrepancies were resolved, and the consensus code was assigned to the task.
Data Analysis
Following data collection and coding, the coding results were summarized to answer the research questions. For the first research question, the distribution of tasks with respect to cognitive demand and the inclusion of technology was examined in order to identify differences or similarities between those tasks that used technology and those that did not and to discern any association of the use of technology with low- or high-level tasks.
The coding results were summarized with respect to the way that technology was used (amplifier, reorganizer, or both) during the set up and implementation phases of low-level tasks for the second research question and with respect to high-level tasks for the third research question. These coding results were used to observe patterns in the data that could guide qualitative analysis.
For example, one hypothesis regarding the second research question was that the use of technology as an amplifier would be associated with low-level cognitive demand tasks. However, the summary of the coding results revealed that, although the use of technology as an amplifier was often associated with low-level tasks across sites, a number of high-level tasks also used technology as an amplifier. Thus, the set of tasks using technology as an amplifier were analyzed qualitatively in order to understand the role that technology played in these tasks and how it was related to the thinking demands of the task.
Lesson observation field notes, student work, and interview transcripts were analyzed to identify how particular actions that students (or the teacher) performed with technological tools were related to interactions between students or between student and teacher, the work students produced, and the teacher’s interpretation of students’ thinking and use of technology. In order to use this qualitative analysis to characterize the role of technology in tasks of varying cognitive demand, the constant comparative method (Glaser, 1965) was used in analyzing different tasks in the same classroom, as well as across classrooms.
Results
The primary focus of this study was on ways the use of technology was correlated with the cognitive demand of the mathematical tasks within which that use was situated and the meaning of those associations. Answering the first research question required generalizing across the set of 63 tasks by examining how the distribution of low- and high-level tasks related to the use of technology. Qualitative data were compiled to construct a representation of the observed lessons, which were then coded with respect to the cognitive demand and use of technology.
Thus, the results reported for the first research question are not qualitative in nature, but qualitative data were used to generate them. Results regarding the role of technology in low-level and high-level tasks include reporting patterns in the coding of these subsets of tasks, as well as qualitative examples from the data that exemplify the conclusions and provide insight into how technology played the role that it did.
The Use of Technology in Relation to Cognitive Demand
The results of the coding of tasks in terms of the cognitive demand and the inclusion of technology are reported in Tables 2 and 3.
Table 2
Distribution of Tasks During Set-Up
Set-Up | No Technology | Technology | Total |
| Low-level | 12 | 25 | 37 |
| High-level | 3 | 23 | 26 |
Table 3
Distribution of Tasks During Implementation
Implementation | No Technology | Technology | Total |
| Low-level | 6 | 48 | 54 |
| High-level | 1 | 8 | 9 |
A few trends in the coding results are worth noting and require some explanation. The first is that a large majority of tasks utilized technology in some way, with 48 out of 63 tasks (76%) making use of technology during the set up of the task, and 56 of 63 tasks (89%) using technology during implementation. This trend provides evidence that instructional technologies are becoming ubiquitous in some secondary mathematics classrooms.
Related to this trend is the fact that some tasks were set up by the teacher without any explicit mention of technology as part of the task, but students initiated its use during implementation of the task. Twelve tasks were set up at a low level without technology, but only six tasks were implemented at a low level without technology. For example, students used scientific calculators while solving equations, even though there was no mention of using (or not using) calculators when the task was introduced to the class. This task used technology during implementation but not during set up, explaining the increase from one phase to the next.
The main result that can be gleaned with respect to the first research question is that these teachers set up and implemented more tasks at a low level than at a high level, whether technology was used or not, a result that is consistent with research on trends in U.S. classrooms (Stein et al., 1996; Stein & Lane, 1996; Stigler & Hiebert, 2004; Weiss & Pasley, 2004; Weiss, Pasley, Smith, Banilower, & Heck, 2003).
This general pattern was much more evident during implementation, where six times as many tasks were implemented at a low level than at a high level across both conditions (technology and no technology). However, the fact that these teachers set up almost as many tasks at a high level as at a low level when using technology is a notable exception to this general trend. It suggests that they perceived a certain usefulness of technology in relation to higher cognitive demand tasks.
In addition, teachers were fairly consistent across conditions in their ability to maintain the cognitive demand of a task set up at a high level during implementation. Ms. Jones and Ms. Young implemented all their tasks at a low level, whether technology was used or not, while Mr. Mack and Ms. Lowe both had some success implementing tasks at a high level. Across all sites, the proportion of tasks maintained at a high level during implementation was the same both with and without the inclusion of technology (about one third). Thus, while these teachers set up more high-level tasks when using technology, they did not maintain the cognitive demand of these tasks during implementation with greater success when technology was used than when it was not.
Many researchers have noted that teachers use technology in a way that is consistent with their current teaching practice (Cuban, Kirkpatrick, & Peck, 2001; Earle, 2002; Farrell, 1996; Galbraith, 2006; Kastberg & Leatham, 2005; Kendal & Stacey, 2001; Monaghan, 2004; Norton, McRobbie, & Cooper, 2000; Russell, Bebell, O’Dwyer, & O’Connor, 2003). These results demonstrate further evidence of this trend along the dimension of practice constituted by the choice of mathematical tasks with which teachers engage their students.
The Role of Technology in Low-Level Tasks
Table 4 shows the distribution of tasks set up or implemented at a low level across the use of technology (no technology, amplifier use, or both amplifier and reorganizer use).
Table 4
The Distribution of Low-Level Tasks With Respect to Technology Use
Low-Level Tasks | No Technology | Amplifier | Both Amplifier and Reorganizer | Total |
| Set up | 12 | 25 | 0 | 37 |
| Implementation | 6 | 46 | 2 | 54 |
One trend present in these data that is not obvious in Table 4 is that many tasks set up to use technology as both an amplifier and reorganizer in a high level task were implemented at a low level using technology as an amplifier only. This trend helps to account for the increase in the number of tasks using technology as an amplifier from set-up to implementation in low-level tasks in Table 4.
In addition, no instances of using technology as a reorganizer only were coded in these data (including high-level tasks), but when technology was used as a reorganizer, it was always in conjunction with its use as an amplifier. Thus, for the sake of simplicity, the terms reorganizer and both amplifier and reorganizer are used interchangeably for the remainder of this article.
The results of the coding of tasks that utilized technology demonstrate that the use of technology as an amplifier was generally associated with low-level tasks, although it was used in some high-level tasks as well. The role of technology in low-level tasks varied, and thus, the discussion of its role in these tasks is separated into two parts: (a) tasks that were set up and implemented at a low level and (b) tasks that were set up at a high level and declined to a low level during implementation.
Tasks Set Up and Implemented at a Low Level. Table 4 demonstrates a correlation of amplifier use with low-level tasks, especially during implementation. However, what these data do not reveal is whether these uses of technology somehow supported or contributed to the cognitive demand of the tasks within which they appeared. Qualitative analysis of the tasks that used technology as an amplifier revealed that the amplifier use of technology was not causally related to the cognitive demand of these tasks.
Within the sample of technology-enhanced tasks set up at a low level, the use of technology was always as an amplifier, as Table 4 demonstrates. In most cases, these tasks involved using an IWB for a class lecture and practice problems.
In all 25 tasks set up at a low level with technology, the IWB was used either by itself or in conjunction with calculators or DGS. It was used to display lecture notes or practice problems and to project a worksheet while discussing problems or solutions. In many cases, teachers took electronic copies of the textbook and copied and pasted them into presentation software files and also used these to create handouts for students. In some cases, teachers used it in conjunction with DGS in order to provide a dynamic demonstration or example. What these examples have in common is that the IWB was used to display text and images that everyone in the classroom could see.
Other cases of using technology as an amplifier during set-up involved the use of a calculator for computations while completing worksheets. In terms of the cognitive demand, these teachers primarily used technology as an amplifier in the set-up of low-level tasks as a medium for the display of content to be memorized, procedures to be learned, or problems for which the recall of facts or the execution of procedures was desired.
The results of the qualitative analysis of these tasks suggests that the association of the use of technology as an amplifier with low-level cognitive demand tasks says more about the decisions these teachers made in selecting tasks than it does about the use of technology. The role of technology in these tasks is merely a medium or computational aid for the task that the teacher had chosen to enact with students in a given lesson.
The use of technology did not contribute to the low cognitive demand of these tasks, as in these cases the task would have been implemented at a low level even if technology were not used. Further evidence of the claim that amplifier use of technology did not contribute to the low-level demand of these tasks is given by the fact that technology was used as an amplifier within high-level tasks. Thus, when technology was used as an amplifier, it seemed incidental to the cognitive demand of the task.
Tasks That Declined to a Low Level During Implementation. The set of tasks implemented at a low level included tasks that were set up at a low level as well as others set up at a high level. Consistent with research on cognitive demand (Stein & Lane, 1996; Stein et al., 1996), all of the tasks set up at a low level remained at a low level during implementation. However, many tasks set up at a high level were implemented at a low level as well, a trend also consistent with the research in this area (Henningsen & Stein, 1997; Stein et al., 1996; Stigler & Hiebert, 2004).
Although the use of technology as an amplifier was associated with the low-level implementation in these tasks as well, the fact that technology was intended to be used as both an amplifier and a reorganizer in a high-level task makes the role of technology in these tasks different than when it is used in the set-up of a low-level task.
Table 5 summarizes the tasks that these teachers set up at a high level using DGS as both an amplifier and a reorganizer and implemented at a low level using technology as an amplifier only. DGS has the ability to display accurate and precise representations of mathematical objects that can be manipulated by the user, and these capabilities allow students to interact directly with mathematical representations and to explore and discover the properties of these objects. This pattern suggests that for these teachers the purpose of using technology as a reorganizer was strongly related to engaging students with high-level cognitive demand tasks.
Table 5
Tasks Using Technology That Declined During Implementation
Teacher | Technology | Task Description |
Ms. Jones | GSP | Teacher leads the class in using GSP in order to determine how a line segment connecting two sides of a triangle can create a similar triangle within the given triangle. |
| Students use GSP to explore the relationship between the lengths of the sides of a triangle, i.e., the Triangle Inequality Theorem. | ||
| Students use GSP to individually explore the relationship between the angles formed by parallel lines cut by a transversal and between the angles formed by intersecting lines. | ||
| Students use GSP to discover that trig ratios (sine, cosine, and tangent) depend only on the angles and not on the side lengths. | ||
Ms. Young | GeoGebra | Students use dynamic GeoGebra applet to discover angle relationships formed by parallel lines cut by a transversal. |
| Students use a dynamic GeoGebra applet to discover that the sum of the interior angles of a triangle equal 180. | ||
GeoGebra | Students use GeoGebra to construct a triangle and an exterior angle to discover that the sum of the two remote interior angles is equal to the exterior angle. | |
GSP | Students use GSP to explore the relationship between the lengths of the sides of a triangle, i.e., the Triangle Inequality Theorem. | |
Mr. Mack | IWB | The teacher uses the IWB to demonstrate how to estimate fractions and sums using a number line and benchmark fractions and decimals. |
With the exception of one task used by Mr. Mack, these tasks were all set up to use DGS as both an amplifier and a reorganizer in a high-level task, but were implemented using it as an amplifier only at a low level.
Given the documented difficulty in maintaining the cognitive demand of a task set up at a high level during implementation (Henningsen & Stein, 1997; Stein et al., 1996; Stigler & Hiebert, 2004), the use of technology in these tasks was not necessarily the cause of the observed decline. Nonetheless, the decline of the thinking demands of these tasks coincided with students using technology as an amplifier only.
Qualitative analysis of these tasks suggests that, while there is a meaningful connection between the decline of these tasks and the use of technology as an amplifier only, it is not necessarily a cause-and-effect relationship. Rather, the use of DGS as a reorganizer was connected with the high cognitive demand of these tasks as set up, and thus when students failed to use it as a reorganizer, they also did not engage in the high-level thinking demands of the task.
The tasks that declined during implementation required students to construct, measure, and manipulate representations of mathematical objects in order to explore their properties. The high-level thinking required by these tasks generally consisted of making mathematically meaningful observations, generalizations, or conjectures.
The thinking entailed in dragging representations of mathematical objects can be complex (Hollebrands et al., 2008), and the use of technology can support students’ ability to make conjectures by providing numerous examples to analyze as the basis for a conjecture. However, in order for students to use technology in this way, they must understand the importance of examining a variety of examples, determine what is mathematically meaningful to look for across those examples, and understand how to make a mathematically precise statement as a conjecture.
Furthermore, students must recognize the importance of strategically manipulating objects in order to test a conjecture and look for counterexamples and the difference between a conjecture and a proof. These behaviors were precisely the ones in which students failed to engage. They constructed, measured, and manipulated figures, but there was no evidence that the majority of students engaged in this sort of high-level thinking.
For example, in Ms. Jones’ class, students created triangles and measured side lengths in order to explore the Triangle Inequality Theorem (the sum of the lengths of any two sides of a triangle is always greater than the length of the third side), as shown in Video 1. However, when asked if it were possible to create a triangle in which the sum of two side lengths could be less than the third or equal to it, a number of students replied “Yes,” and few students wrote a conjecture about the relationship between the lengths of the sides. Thus, they created, measured, and manipulated triangles, but did not make mathematically relevant observations or generalizations or make and test conjectures, behaviors that constituted the high-level aspect of the task.
Video 1. Using Geometer’s Sketchpad to explore the Triangle Inequality Theorem.
Ms. Young’s students experienced similar issues when engaging with the Triangle Inequality Theorem task in Geometer’s Sketchpad. Ms. Young reported that she was pleased with how her students were able to construct and measure their triangles correctly, noting that the use of the technology was not problematic for them. That is, students exhibited some proficiency in using the technology as an amplifier.
However, in the postlesson interview she said that her students had “questions about the questions” that they were asked in the worksheet regarding making observations and conjectures. She admitted that her students had little experience with making conjectures in a mathematics class. Her students’ inability to understand the generality of the observations they needed to make in order to make and test conjectures seemed to prevent them from using DGS in a way that would support that type of thinking.
These examples were typical of what occurred in Ms. Jones’ and Ms. Young’s classrooms during these tasks. Students constructed, measured, and dragged, and thus, technology was used as an amplifier by making students’ work more precise and efficient. Most students, however, did not utilize this work with the technology to engage in the high-level thinking involved in looking for patterns or invariance or making and testing conjectures.
These teachers seemed to underestimate the support that students would need in connecting their work with DGS to the mathematical thinking and behavior required by the task. The capabilities of DGS can support high-level thinking, but nothing about the use of a DGS for an exploratory task causes students to engage in high-level thinking.
If students have never been asked to make a conjecture before, providing them with technological tools that support making conjectures will not necessarily result in their ability to do so. Ultimately, when technology is used as both an amplifier and a reorganizer, teachers must support the shift entailed by its use as a reorganizer. In these cases, students’ inability to use technology as a reorganizer, as well as their failure to engage with these tasks at a high level, both seemed more related to their lack of understanding of the mathematical thinking and behaviors that were the goal of the task than to any role that the technology played directly. Thus, implementing high-level tasks at a high level using technology may have less to do with the technology than it does with support for students’ high-level engagement.
Many classroom-based factors have the potential to influence whether or not a task set up at a high level was implemented at a high level (c.f., Stein et al., 1996; Stein et al., 2009). In addition to these factors, the support needed by students when engaging in technology-enhanced tasks must also take into account the role that technology is intended to play in the high-level thinking aspects of the task (Sherman, 2012).
Tasks Set Up and Implemented at a High Level
Consistent with research (Stein & Lane, 1996; Stein et al., 1996; Henningsen & Stein, 1997), a minority of the tasks set up at a high level remained at a high level during implementation, as shown in Table 6. Unlike low-level tasks, which were exclusively set up using technology as an amplifier, high-level tasks were set up and implemented using technology in both ways, that is, as amplifier and as amplifier and reorganizer, although more often the latter. The role of technology in these tasks varied between these two uses of technology, and thus, each is discussed separately in this section.
Table 6
The Distribution of High-Level Tasks With Respect to Technology Use
High-Level Tasks | No Technology | Amplifier | Both Amplifier and Reorganizer | Total |
| Set up | 3 | 7 | 16 | 26 |
| Implementation | 1 | 2 | 6 | 9 |
High-Level Tasks Using Technology as an Amplifier. Seven tasks used technology as an amplifier to set up a high-level task. In general, the IWB was used as an amplifier to display the statement or description of a high-level task. For example, Mr. Mack displayed the Spice Problem from the sixth-grade Connected Mathematics 2 curriculum (Lappan, Fey, Fitzgerald, Friel, & Phillips, 2006) by cutting and pasting and rewriting the problem statements from an electronic version of the text into an IWB software file.
The problem was set up as a high-level task. In the context of purchasing spices needed for recipes students were to use their background knowledge of fractions and fraction sums in order to invent a method for subtracting mixed numbers when the fractional part of the subtrahend is larger than the fractional part of the minuend. Mr. Mack used the IWB to support a class discussion of student strategies on this task, inviting students to the board or calling on them to share their strategies and using a virtual IWB pen to write on copies of the problems displayed on the IWB.
Similar to the use of the IWB as an amplifier in tasks set up at a low level, the use of the technology was not related to the cognitive demand of the task. It was simply a medium for communicating or describing a task that would have had the same cognitive demand if it were displayed or communicated using another medium. The fact that a large majority of the tasks that used technology as an amplifier were set up at a low level appears to reflect the fact that, in general, these teachers used more low-level than high-level tasks with their students, regardless of whether or not technology was included.
High-Level Tasks Using Technology as an Amplifier and a Reorganizer. The sample of tasks both set up and implemented at a high level, in which technology was used as both an amplifier and a reorganizer, is shown in Table 7. In conjunction with the tasks shown in Table 6, it comprises the set of tasks that were set up at a high level using technology as a reorganizer. The fact that no task was set up at a low level using technology as a reorganizer is significant, as it indicates that these teachers perceived affordances of technology, DGS in particular, that would support students’ high-level thinking. The fact that only Mr. Mack’s and Ms. Lowe’s students engaged with these tasks at a high level during implementation is further evidence that Ms. Jones’ and Ms. Young’s students’ low-level engagement during implementation is likely more related to classroom pedagogy than technological factors.
Table 7
Tasks Set up and Implemented at a High Level Using Technology
|
In general, the use of technology as an amplifier and reorganizer in these tasks involved offloading tedious or time consuming constructions or measurements to technology in order to allow students to focus on a high-level aspect of the task. (Mr. Mack’s use of the IWB to provide an interactive figure to support a discussion of students’ strategies on this task was unique and is not discussed in detail here.)
The purpose of using technology in these tasks was for students to construct meaning for a mathematical concept or procedure or to engage in mathematical behaviors, such as observing, reasoning, generalizing, and conjecturing. Although Ms. Jones and Ms. Young also used DGS in the set-up of high-level tasks, Ms. Lowe’s class provides some insight into how that intended purpose was fulfilled by students during implementation.
Ms. Lowe generally created her own worksheet to guide students in using GeoGebra individually at their own computers for most of the period in order to investigate the properties of triangles. A particular task that she enacted with her students involved using GeoGebra to investigate the properties of the centroid of a triangle, that is, the intersection of the medians of a triangle. (The median is the segment connecting the midpoint of a side of a triangle to the opposite vertex.) The worksheet guided students to construct a triangle and its medians, construct the centroid, measure the segments from the vertex to the centroid and from the centroid to the midpoint of the opposite side (see an example at http://www.geogebratube.org/student/m122153), and then record these measurements in a table in order to look for a relationship and make a conjecture.
The relationship students were intended to discover is that the segment from the midpoint to the centroid is one third of the length of the median, and the segment from the centroid to the opposite vertex is two thirds of the length of the median. In this case, the opportunity for each student to drag and explore the properties of the medians was directly connected to the cognitive demand of the task, as it provided a means for students to look for patterns and invariance in the sketch.
As an example of the type of thinking that students engaged in while working on the task, the following conversation was observed between two students:
[Nick and Brian are dragging their figures and discussing what it is that they’re supposed to be noticing.]
Nick: There are lots of things to notice.
Brian: Yeah, but most of them are obvious.
Nick: I’m going to make it a right triangle. What would that do? It would stay at the center of the triangle, right?
Brian: Look at this.
[Brian shows Nick his table, pointing out the 6.17 and the 3.08.]
Brian: This one is almost exactly double that one.
Nick: You can’t make assumptions from one triangle.
[Both start dragging their triangles.]
Nick: I see something like that, but if you stretch it far enough…
[They continue dragging their triangles and looking at the measurements.]
Nick: One is always half of the other.
Brian: The distance from the vertex is always double the distance to the midpoint.
Ms. Lowe: Change it, see if you can disprove it.
[Starting over with a new triangle, Brian begins to measure the distances from the centroid to the vertex and from the centroid to the midpoint for each median.]
Brian: [as he measures each segment] That is double that, and that is double that, and that is double that.
Nick drags his figure.
Nick: Yes, it does stand true.
(Field note, 2/7/11)
This excerpt demonstrates both the amplifier and reorganizer uses of technology in this task. Students constructed a triangle, the medians of the triangle, and the centroid quickly and precisely. Students measured and labeled the angle measures, the lengths of the medians, and the lengths of the segments. Most students had completed this part of the task within 10 minutes. While students might be able to construct the centroid of a triangle and use a protractor and ruler to make the same measurements, this could be difficult for most students to do accurately in 10 minutes. Furthermore, by dragging the triangle, students are essentially creating many triangles and their medians and centroids.
However, dragging does more than create multiple examples quickly. One can observe, for example, how the centroid moves in response to a vertex being dragged, that is, how the location of the centroid changes from an acute triangle, to a right triangle, to an obtuse triangle, and back again. This sort of real-time motion of one object in relation to another is simply not possible in a pencil-and-paper environment and is a capability of DGS that supports its use as a reorganizer by students.
In the excerpt, for example, students were not focused on making the necessary measurements, but on using them to discern regularities in the behavior of the segments and on understanding what they mean. By saying, “I’m going to make it a right triangle. What would that do? It would stay at the center of the triangle, right?” Nick illustrated the open-ended nature of directly manipulating an object created within a DGS. Many possibilities exist in terms of how to drag the object.
His quotation also reveals the making and testing of conjectures that is inherent in the development of a more strategic investigation of an object using dragging. Students must consider the purpose of dragging in terms of an overarching goal, what information would be helpful in achieving that goal, and what sort of dragging might provide that information. Students must then assess if the object behaved in the anticipated manner and, if not, why, and what should the next move be in light of this information?
The technology acts as a reorganizer by supporting these students’ focus on looking for relationships and making and testing conjectures. Nick’s statement that one “can’t make assumptions from one triangle,” and the subsequent dragging of his triangle indicated that he understood the goal of this task to be a relationship that could be generalized. It also demonstrates that he understood the affordances of dragging the figure in relation to that goal. This assertion was further confirmed after Brian pointed out the relationship in the median segments while helping him to measure those segments, and Nick dragged the triangle to test the claim before agreeing with it.
Another important element of this task was the relative absence of Ms. Lowe in Brian and Nick’s investigation. She appeared briefly, but only after they had made and tested their conjecture, and only to advance the students’ thinking. This concrete example shows how the use of technology supports independent investigation by students, a goal that Ms. Lowe cited for having students engage in these types of tasks.
The description of this task is consistent with the way in which GeoGebra was used in the four other tasks implemented at a high level by Ms. Lowe. A number of factors supported students’ high-level engagement in Ms. Lowe’s class (Sherman, 2012), but the focus here is the role of technology in that process. Ultimately, it provided a way for students to interact directly with accurate representations of mathematical objects in order to explore their properties, look for patterns and invariance, and make and test conjectures. A crucial factor related to the use of technology as a reorganizer by students and not just an amplifier is an understanding of the goals of the task and how the tools provided by technology can help to achieve them.
Discussion
Consistent with the results from other studies (Cuban et al., 2001; Doerr & Zangor, 2000; Farrell, 1996; Kendal & Stacey, 2001; Monaghan, 2004; Norton et al., 2000), these teachers seemed generally to adapt the use of technology in their classrooms to their current practice. Monaghan (2004) noted “a division between those who view technology as something that enables teacher to become less ‘didactic’ in their interactions with students, and those who perceive change in practice as problematic” (p. 328).
In particular, he pointed out a discrepancy between the claim that the introduction of technology into classrooms will “naturally” result in a shift in a teacher’s traditional role as the locus of mathematical knowledge and authority to a facilitator or catalyst of students’ mathematical activity and the research on technology use by teachers that demonstrates the process is much more complex and problematic.
By distinguishing between the set-up and implementation phases, the Mathematical Tasks Framework (Stein & Smith, 1998) provides a more nuanced interpretation of these results. Although a large majority of the tasks were implemented at a low level, these data seem to point to an attempt by these teachers to use technology to engage students in high-level tasks during the set-up phase. The fact that almost 50% of tasks using technology were set up at a high level versus about 20% of nontechnology tasks provides evidence of this fact.
These teachers appeared to be making an attempt to enact instruction that departed from their established teaching practice. During implementation, however, the level of students’ mathematical thinking was similar to what was observed when technology was not used.
Another interpretation of these results, then, is that when these teachers adapted the use of technology to their current practice it was used as an amplifier. The association of amplifier use with low-level tasks revealed in these data seem to be mediated through the teachers, that is, the selection of the task was the primary factor in the cognitive demand when technology was used as an amplifier.
On the other hand, when these teachers chose to set up high-level tasks with their students, there is evidence that the use of technology as a reorganizer was perceived as supporting that instructional goal. The set-up of a high-level task was strongly associated with this use of technology. Thus, using technology as a reorganizer may have indicated an attempt to break with current practice, even if those efforts failed during implementation.
Implications for Teacher Education
The results of this study support the following claim in the Technology Principle of the Principles and Standards for School Mathematics (NCTM, 2000):
Technology is not a panacea. As with any teaching tool, it can be used well or poorly. Teachers should use technology to enhance their students’ learning opportunities by selecting or creating mathematical tasks that take advantage of what technology can do efficiently and well. (p. 25)
Given the documented difficulty that teachers have in selecting high-level cognitive demand tasks and maintaining the demand of tasks set up at a high level during implementation (Henningsen & Stein, 1997; Stein et al., 1996; Stigler & Hiebert, 2004), and the quality of mathematical learning that students exhibit as a result of engaging with high-level tasks (Boaler & Staples, 2008; Stein & Lane, 1996), it is important to understand how the use of technology can support this endeavor. The use of technology as a reorganizer as exhibited in the sample of tasks analyzed here demonstrates that the use of DGS can play an important role in the cognitive demand of tasks in which students are required to investigate the properties of mathematical objects by making observations, generalizations, conjectures, and connections to other mathematical ideas or objects.
Although only one of the three teachers was successful in implementing these tasks at a high level, there is evidence that these three teachers perceived a certain usefulness of DGS to support the high-level thinking goals. The majority of tasks set up at a high level involved using technology in this way, and no tasks were set up at a high level using technology as an amplifier.
This fact is significant, as research has shown that students who are exposed to high-level tasks during set-up demonstrated more meaningful learning of mathematics than those who were not, even if the thinking demands declined during implementation (Stein & Lane, 1996). Furthermore, the differences in implementation are likely accounted for more by classroom factors, such as clear expectations, support by the teacher that did not remove the thinking required by the task, and accountability for high-level thinking. The use of DGS as a reorganizer has the potential to support teachers who are interested in student-centered instruction that requires students to think and reason mathematically.
These results also demonstrate that merely introducing technology into the classroom does not bring about that change on its own. If students are asked to engage in activity and thinking with which they have little or no experience, to do and learn mathematics in a qualitatively different manner than what they are accustomed to, then the inclusion of a technology that can support that activity will likely have little effect. Students need to have the desired high-level mathematical thinking and behavior modeled and must be supported in using new tools to engage in it.
Thus, teachers who have not yet learned how to engage their students in high cognitive demand tasks successfully will not magically be able to do so by introducing a new tool, even if that tool has the potential to support that goal. Indeed, introducing a new tool into the learning environment is likely to make such an endeavor more complex. Holistic professional development is needed that integrates the use of technological tools with engaging students in high-level mathematical thinking.
Research has demonstrated that teachers can be prepared to choose, set up, and implement tasks of a higher cognitive demand (Boston & Smith, 2009). In light of the results of the present study, a more modest goal for the use of technology for mathematics instruction is that it can support teachers who are attempting to transform their practice to a more student-centered, problem-solving approach.
The remaining question, then, is how to incorporate the use of technology in professional development and teacher education in a way that would support that goal. The results of this study suggest that focusing on technology use is likely to have little effect if teachers’ goals and instructional strategies are unaddressed. The answer involves helping teachers to weave the use of technological tools into a more student-centered practice, so that the use of technological tools aligns with and supports a learning environment that values student investigation and exploration.
The present analysis builds on previous work that makes use of the amplifier and reorganizer distinction (Ben-Zvi, 2000; Goos et al., 2003; Laborde, 2002; Lee & Hollebrands, 2008; Zbiek et al., 2007), but extends the distinction by considering how technology might act as an amplifier or reorganizer during the implementation of classroom tasks. The amplifier and reorganizer metaphor may help to add specificity to the distinction between superficial and meaningful use of technology in mathematics classrooms by considering the role of technology with respect to the mathematical thinking demands of a task.
An understanding of this distinction may be an important element of mathematics teachers’ technological pedagogical content knowledge (Koehler & Mishra, 2008; Mishra & Koehler, 2006; Niess, 2005; Niess et al., 2009) by providing a way to examine critically the role of technology in the tasks they choose to enact with their students.
Evidence from work with preservice teachers in a secondary methods course suggests that they were able to understand and make use of the amplifier and reorganizer distinction to evaluate, select, and develop technology-enhanced mathematical tasks (Sherman, 2013). Research is needed to determine how an understanding of this distinction might influence in-service mathematics teachers’ selection and implementation of high-level cognitive demand classroom tasks, perhaps by making the connection between these two frameworks more explicit. An understanding of precisely how the use of technology as a reorganizer can support students’ high-level mathematical thinking may better prepare teachers to support that endeavor during implementation.
References
Ben-Zvi, D. (2000). Toward understanding the role of technological tools in statistical learning. Mathematical Thinking and Learning, 2(1&2), 127–155.
Boaler, J., & Staples, M. (2008). Creating mathematical futures through an equitable teaching approach: The case of Railside School. The Teachers College Record, 110(3), 608–645.
Boston, M. D., & Smith, M. S. (2009). Transforming secondary mathematics teaching: Increasing the cognitive demands of instructional tasks used in teachers’ classrooms. Journal for Research in Mathematics Education, 40(2), 119–156.
Boutell, M., & Clifton, C. (2011). SPLICE: Self-paced learning in an inverted classroom environment. In Proceedings of the 42nd ACM Technical Symposium on Computer Science Education. New York, NY: Association for Computing Machinery.
Burrill, G., Allison, J., Breaux, G., Kastberg, S., Leatham, K., & Sanchez, W. (2002). Handheld graphing technology in secondary mathematics: Research findings and implications for classroom practice. Retrieved from the Texas Instruments website: http://education.ti.com/sites/UK/downloads/pdf/References/Done/Burrill,G.%20(2002).pdf
Chazan, D. (1999). On teachers’ mathematical knowledge and student exploration: A personal story about teaching a technologically supported approach to school algebra. International Journal of Computers for Mathematical Learning, 4, 121–149.
Chazan, D. (2000). Toward a “conceptual understanding” of school algebra. New York, NY: Teachers College Press.
Common Core State Standards Initiative. (2010). Common core state standards (Mathematics standards). Retrieved from http://www.corestandards.org/the-standards/mathematics
Cuban, L., Kirkpatrick, H., & Peck, C. (2001). High access and low use of technologies in high school classrooms: Explaining an apparent paradox. American Educational Research Journal, 38(4), 813.
Cuoco, A., Goldenberg, E. P., & Mark, J. (1996). Habits of mind: An organizing principle for mathematics curricula. Journal of Mathematical Behavior, 15, 375–402.
Deslauriers, L., Schelew, E., & Wieman, C. (2011). Improved learning in a large-enrollment physics class. Science, 332(6031), 862–864.
Doerr, H. M., & Zangor, R. (2000). Creating meaning for and with the graphing calculator. Educational Studies in Mathematics, 41(2), 143–163.
Earle, R. S. (2002). The integration of instructional technology into public education: Promises and challenges. Educational Technology, 42(1), 5–13.
Farrell, A. M. (1996). Roles and behaviors in technology-integrated precalculus classrooms. The Journal of Mathematical Behavior, 15(1), 35–53.
Foertsch, J., Moses, G., Strikwerda, J., & Litzkow, M. (2002). Reversing the lecture/homework paradigm using eTEACH® web-based streaming video software. Journal of Engineering Education, 91(3), 267–274.
Galbraith, P. (2006). Students, mathematics, and technology: Assessing the present–challenging the future. International Journal of Mathematical Education in Science and Technology, 37(3), 277–290.
Gannod, G. C., Burge, J. E., & Helmick, M. T. (2008). Using the inverted classroom to teach software engineering. In Proceedings of the 30th International Conference on Software Engineering (pp. 777–786). New York, NY: Association for Computing Machinery.
Glaser, B. G. (1965). The constant comparative method of qualitative analysis. Social Problems, 12(4), 436–445.
Goos, M., Galbraith, P., Renshaw, P., & Geiger, V. (2003). Perspectives on technology mediated learning in secondary school mathematics classrooms. The Journal of Mathematical Behavior, 22(1), 73–89.
Heid, M. K. (1988). Resequencing skills and concepts in applied calculus using the computer as a tool. Journal for Research in Mathematics Education, 19(1), 3–25.
Heid, M. K. (1997). The technological revolution and reform of school mathematics. American Journal of Education, 106, 5–61.
Heid, M. K., & Blume, G. W. (Eds.). (2008). Research on technology in the teaching and learning of mathematics: Research syntheses (Vol. 1). Charlotte, NC: Information Age Publishing.
Henningsen, M. A., & Stein, M. K. (1997). Mathematical tasks and student cognition: Classroom-based factors that support and inhibit high-level mathematical thinking and reasoning. Journal for Research in Mathematics Education, 28(5), 524–549.
Hollebrands, K. F., Conner, A. M., & Smith, R. C. (2010). The nature of arguments provided by college geometry students with access to technology while solving problems. Journal for Research in Mathematics Education, 41(4), 324–350.
Hollebrands, K. F., Laborde, C., & StraBer, R. (2008). Technology and the learning of geometry at the secondary level. In M. K. Heid & G. W. Blume (Eds.), Research on technology in the teaching and learning of mathematics: Research syntheses (Vol. 1, pp. 155–205). Charlotte, NC: Information Age Publishing.
Huntley, M. A., Rasmussen, C. L., Villarubi, R. S., Sangtong, J., & Fey, J. T. (2000). Effects of standards-based mathematics education: A study of the Core-Plus Mathematics Project Algebra and Functions strand. Journal for Research in Mathematics Education, 31(3), 328–61.
Judson, P. T. (1990). Elementary business calculus with computer algebra. Journal of Mathematical Behavior, 9(2), 153–157.
Kastberg, S., & Leatham, K. (2005). Research on graphing calculators at the secondary level: Implications for mathematics teacher education. Contemporary Issues in Technology and Teacher Education, 5(1), 25–37. Retrieved from https://citejournal.org/vol5/iss1/mathematics/article1.cfm
Kendal, M., & Stacey, K. C. (2001). The impact of teacher privileging on learning differentiation with technology. International Journal of Computers for Mathematical Learning, 6(2), 143–165.
Koehler, M. J., & Mishra, P. (2008). Introducing technological pedagogical content knowledge. In AACTE Committee on Innovation and Technology (Ed.), Handbook of technological pedagogical content knowledge (TPCK) for educators (pp. 3–29). New York, NY: Routledge.
Laborde, C. (2002). Integration of technology in the design of geometry tasks with Cabri-Geometry. International Journal of Computers for Mathematical Learning, 6(3), 283–317.
Lage, M. J., Platt, G. J., & Treglia, M. (2000). Inverting the classroom: A gateway to creating an inclusive learning environment. The Journal of Economic Education, 31(1), 30–43.
Lappan, G., Fey, J., Fitzgerald, W., Friel, S., & Phillips, E. D. (2006). Connected mathematics 2: Grade 6. Pearson Prentice Hall.
Lee, H. S., & Hollebrands, K. F. (2008). Preparing to teach mathematics with technology: An integrated approach to developing technological pedagogical content knowledge. Contemporary Issues in Technology and Teacher Education, 8(4), 326–341. Retrieved from https://citejournal.org/vol8/iss4/mathematics/article1.cfm
Mishra, P., & Koehler, M. J. (2006). Technological pedagogical content knowledge: A framework for teacher knowledge. Teachers College Record, 108(6), 1017–1054.
Monaghan, J. (2004). Teachers’ activities in technology-based mathematics lessons. International Journal of Computers for Mathematical Learning, 9(3), 327–357.
Moore, A. J., Gillett, M. R., & Steele, M. D. (2014). Fostering student engagement with the flip. Mathematics Teacher, 107(6), 420.
National Council of Teachers of Mathematics. (1991). Professional standards for teaching mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (2009). Focus in high school mathematics: Reasoning and sense making. Reston, VA: Author.
Niess, M. L. (2005). Preparing teachers to teach science and mathematics with technology: Developing a technology pedagogical content knowledge. Teaching and Teacher Education, 21, 509–523.
Niess, M. L., Ronau, R. N., Shafer, K. G., Driskell, S. O., Harper, S. R., Johnston, C., … Kersaint, G. (2009). Mathematics teacher TPACK standards and developmental model. Contemporary Issues in Technology and Teacher Education, 9(1), 4–24. Retrieved from https://citejournal.org/vol9/iss1/mathematics/article1.cfm
Norton, S., McRobbie, C. J., & Cooper, T. J. (2000). Exploring secondary mathematics teachers’ reasons for not using computers in their teaching: Five case studies. Journal of Research on Computing in Education, 33(1), 87–109.
Novak, G. M., Patterson, E. T., Gavrin, A. D., Christian, W., & Forinash, K. (1999). Just in time teaching. American Journal of Physics, 67, 937.
O’Callaghan, B. R. (1998). Computer-intensive algebra and students’ conceptual knowledge of functions. Journal for Research in Mathematics Education, 29(1), 21–40.
Palmiter, J. R. (1991). Effects of computer algebra systems on concept and skill acquisition in calculus. Journal for Research in Mathematics Education, 22(2), 151–156.
Pea, R. D. (1985). Beyond amplification: Using the computer to reorganize mental functioning. Educational Psychologist, 20(4), 167–182.
Pea, R. D. (1987). Cognitive technologies in mathematics education. In A. H. Schoenfeld (Ed.), Cognitive science and mathematics education (pp. 89–122). Hilldale, NJ: Erlbaum.
Peressini, D., & Knuth, E. J. (2005). The role of technology in representing mathematical problem situations and concepts. In W. J. Masalski & P. C. Elliott (Eds.), Technology-supported mathematics learning environments, 2005 Yearbook of the National Council of Teachers of Mathematics (pp. 277–290). Reston, VA: National Council of Teachers of Mathematics.
Picciotto, H. (2010). Why I use interactive whiteboards. Mathematics Teacher, 104(4), 250–253.
Prober, C. G., & Heath, C. (2012). Lecture halls without lectures—a proposal for medical education. New England Journal of Medicine, 366(18), 1657–1658.
Romberg, T. A. (1994). Classroom instruction that fosters mathematical thinking and problem solving: Connections between theory and practice. In A. H. Schoenfeld (Ed.), Mathematical thinking and problem solving (pp. 287–304). Hillsdale, NJ: Erlbaum.
Russell, M., Bebell, D., O’Dwyer, L., & O’Connor, K. (2003). Examining teacher technology use: Implications for preservice and inservice teacher preparation. Journal of Teacher Education, 54(4), 297–310.
Schwarz, B. B., & Hershkowitz, R. (1999). Prototypes: Brakes or levers in learning the function concept? The role of computer tools. Journal for Research in Mathematics Education, 30(4), 362–389.
Sherman, M.F. (2012). Supporting students’ mathematical thinking during technology-enhanced investigations using DGS. In D. Martinovic, D. McDougall, & Z. Karadag (Eds.), Technology in mathematics education: Contemporary issues. Santa Rosa, CA: Informing Science Institute.
Sherman, M.F. (2013). Supporting teachers’ understanding of the role of technology in mathematics instruction: The amplifier and reorganizer metaphor. Paper presented at the annual conference of the Association of Mathematics Teacher Educators, Orlando, FL.
Stein, M. K., Grover, B. W., & Henningsen, M. A. (1996). Building student capacity for mathematical thinking and reasoning: An analysis of mathematical tasks used in reform classrooms. American Educational Research Journal, 33(2), 455–488.
Stein, M. K., & Lane, S. (1996). Instructional tasks and the development of student capacity to think and reason: An analysis of the relationship between teaching and learning in a reform mathematics project. Educational Research and Evaluation, 2(1), 50–80.
Stein, M. K., & Smith, M. S. (1998). Mathematical tasks as a framework for reflection: From research to practice. Mathematics Teaching in the Middle School, 3(4), 268–75.
Stein, M. K., Smith, M. S., Henningsen, M. A., & Silver, E. A. (2009). Implementing standards-based mathematics instruction: A casebook for professional development (2nd ed.). New York, NY: Teachers College Press.
Stigler, J. W., & Hiebert, J. (2004). Improving mathematics teaching. Educational Leadership, 61(5), 12–17.
Strayer, J. F. (2012). How learning in an inverted classroom influences cooperation, innovation and task orientation. Learning Environments Research, 15(2), 171–193.
Suh, J. (2010). Leveraging cognitive technology tools to expand opportunities for critical thinking in elementary mathematics. Journal of Computers in Mathematics and Science Teaching, 29(3), 14.
Weiss, I. R., & Pasley, J. D. (2004). What is high-quality instruction? Educational Leadership, 61(5), 24–28.
Weiss, I. R., Pasley, J. D., Smith, P. S., Banilower, E. R., & Heck, D. J. (2003). Looking inside the classroom: A study of K-12 mathematics and science education in the United States. Chapel Hill, NC: Horizon Research Inc. Available at http: www.horizonresearch.com
Winterbottom, S. (2007). Virtual lecturing: Delivering lectures using screencasting and podcasting technology. Planet, (18), 6–8.
Zbiek, R. M., Heid, M. K., Blume, G. W., & Dick, T. P. (2007). Research on technology in mathematics education: The perspective of constructs. In F. K. Lester (Ed.), Second handbook of research in mathematics teaching and learning (pp. 1169–1207). Charlotte, NC: Information Age Publishing.
Author Notes
The study reported in this article was part of the author’s dissertation completed at the University of Pittsburgh under the direction of Ellen Ansell. The author wishes to thank James Greeno, Justin Boyle, Charity Cayton, Maryann Huey, Tonia Land, Candace Walkington, and three anonymous reviewers for valuable feedback on earlier versions of this manuscript.
Milan Sherman
Drake University
Email: [email protected]
![]()