The current era of mathematics reform encourages and expects teachers to develop students who view mathematics as a coherent, sense-making endeavor and to use key mathematical processes not only as goals for students but as a means for learning the mathematics content. These current trends in mathematics education can trace their beginnings to the National Council of Teachers of Mathematics (NTCM, 1980) Agenda for Action, with continued emphasis expressed in NCTM’s (1989, 1991, 2000) standards documents, and through today’s Common Core State Standards for Mathematics (CCSSM; Common Core State Standards Initiative, 2010).
Inquiry-based instruction is one effective teaching approach useful in developing these desired student outcomes. Though many definitions of inquiry are used, we view inquiry-based instruction as a student-centered approach, in which students explore mathematical ideas and think critically about the content prior to receiving or developing their own explanations.
In contrast to an inquiry-based approach, most people have experienced mathematics as a set of procedures to be learned, practiced, and automated. Within their own mathematical experiences teachers have rarely been asked to challenge their mathematical understandings; to question why things work the way they do; and to appreciate the beauty, coherence, and value of mathematics.
These types of experiences can have a direct and profound impact upon teachers’ beliefs, conceptions, attitudes, and practices (Fennema & Franke, 1992; Pajares, 1992; Thompson, 1992). If new and different educational outcomes are to be achieved, teachers must be encouraged to try new and different approaches of instruction. A considerable body of research however, has demonstrated that transformation of teachers’ practices is a difficult and complex process (Thompson, 1992).
In addition, teachers are expected to use technology to encourage students to explore mathematics and to foster deeper learning (NCTM, 2000; CCSSO & GSA, 2010). Koehler and Mishra (2009) suggested that technology should be used from the outset of any professional development efforts designed to transform teacher practices. Teachers may then experience mathematics and learn mathematics in ways similar to the way their students will experience and learn mathematics, leading to a more coherent pedagogical approach. However, asking teachers to simultaneously develop their content knowledge, transform their practice to one that is inquiry based, and incorporate new technology into their instruction may prove to be overwhelming.
This paper describes a professional development project, Inquiry in Motion, and our attempts to effect transformative changes in middle grades teachers’ mathematics practices. This report describes the participation of 6 middle school mathematics teachers.
Our goal for the project was to develop and support teachers’ use of technology in teaching mathematics through inquiry. In the first 2 years of the project, we undertook two different approaches in reaching this goal. Both approaches challenged teachers to examine their current content and pedagogical knowledge and the ways in which their knowledge bases interacted as they taught. The first approach developed teachers’ knowledge bases prior to introducing and considering ways that technology could support their instruction and student learning. The second approach immediately introduced technology as a tool for inquiry-based instruction. In our examination of these two approaches, we sought to answer the following questions:
- Prior to training and sustained support on the use of color-graphing calculators, what are middle school teachers’ beliefs about and attitudes toward incorporating graphing calculators into instruction?
- How do middle school teachers’ beliefs and attitudes about incorporating graphing calculators into instruction change as they participate in a professional development program composed of intensive summer training and the availability of multiple support structures throughout the school year?
- Was the strategy of infusing technology contemporaneously with inquiry-based instruction or the strategy of introducing them separately was more effective in producing desired change?
Literature Review and Theoretical Frame
This article reports on a portion of a larger professional development project called Inquiry in Motion (Marshall, Horton, & Smart, 2009; Marshall, Smart, & Horton, 2010; Marshall & Horton, 2011), which has worked with middle grades mathematics and science teachers to develop and assess content-embedded inquiry pedagogy. The project was designed on principles and research on both inquiry instruction and effective professional development.
For this study, we expanded this frame to include other research bases, including teachers’ beliefs and conceptions about mathematics and incorporating technology into instruction and the emerging literature on technological pedagogical content knowledge. This expanded framework guided the formation of our research questions and the professional development supports we provided teachers.
Inquiry Instruction
We take our view of inquiry-based instruction from the National Science Education Standards, in which inquiry-based instruction refers to “the development of understanding through investigation, i.e. asking questions, determining appropriate methods, gathering data, and formulating and communicating logical arguments” (National Research Council, 1996, p. 105). Although this definition was written for science education, it is germane to the pedagogical goals of mathematics educators. A mathematical approach to effective inquiry is the union of the five Process Standards espoused by the NCTM (2000): problem solving, communication, representation, connections and reasoning with content-based objectives. The key facet to an inquiry approach is that students must have opportunity to explore the concepts at hand before receiving a formal explanation of them.
An inquiry-based approach to teaching science has been shown in the literature to be moderately effective in helping students to learn (e.g., Haury, 2002; Shymansky, Kyle & Alport, 1983; Wise & Okey, 1983). Within the Inquiry in Motion project we have seen moderate gains in student performance after Year 1 of teacher participation and significant student gains in science content and processes after Year 2 (Marshall & Horton, 2011).
From a mathematical education standpoint, standards-based teaching approaches have been shown to increase students’ problem solving skills while not significantly influencing (positively or negatively) students’ procedural knowledge. Boaler’s (1998) work is one such example of this result.
Design of Effective Professional Development
The professional development for this project aligns with the work of Loucks-Horsley, Love, Stiles, Mundry, and Hewson (2003): “There is no prescription for which designs are right for which situations” (p. 7). Rather, several things must be considered: teachers’ and students’ knowledge and beliefs, the nature of mathematics teaching and learning, state and national standards, current curricula and assessments, and organizational structures in place to support change. Understanding that these items play a crucial role in the design and delivery of professional development is vital. Further, the role of technology in mathematics was considered in the design of this project.
Neufeld and Roper (2003) suggested that professional learning experiences should be grounded in inquiry, reflection, and experimentation; collaborative; ongoing and supported by modeling; connected to teachers’ current work with students; and supported by a school’s current organizational structure. Additionally, professional developers may assume several roles during professional development (Killion & Harrison, 2006). For the purposes of this project, the researchers served as coaches, mentors, consultants, collaborators, and coordinators.
Teachers’ Beliefs and Conceptions of Mathematics
Much of the earlier research done in the area of teacher beliefs was summarized and synthesized by Thompson (1992). Thompson discussed the differences between beliefs and knowledge. This distinction is important, because these two concepts are often intertwined; teachers often treat their beliefs as knowledge. Further, beliefs can be held with varying levels of conviction and the understanding that not all people may believe the same thing. In contrast, knowledge has the connotation of being universally accepted and is judged solely as being right or wrong.
Researchers have classified and explained the beliefs held by mathematics teachers on the nature of mathematics in several ways (Ernest, 1988; Lerman, 1990; Pajares, 1992; Thompson, 1992). Ernest’s (1988) three different conceptions of mathematics (the problem solving view, the Platonist view, and the instrumentalist view) are connected to the four main models of mathematics teaching offered by Kuhs and Ball (1986), which classify mathematical teaching approaches based upon research on learning and teaching as well as philosophies of education and mathematics.
1) Learner-focused: mathematics teaching that focuses on the learner’s personal construction of mathematical knowledge; 2) Content focused with an emphasis on conceptual understanding: mathematics teaching that is driven by the content itself but emphasizes conceptual understanding; 3) Content-focused with an emphasis on performance: mathematics teaching that emphasizes student performance and mastery of mathematical rules and procedures; and 4) Classroom-focused: mathematics based on knowledge about effective classrooms. (p. 2)
The learner-focused view is most closely associated with an inquiry approach to teaching mathematics. The role of the teacher in this approach is that of a facilitator and a poser of questions and explorations. The second view takes the content as the focus of the classroom and encourages the students to develop understandings of ideas and processes; the lesson is driven not by student inquiry but by a scope and sequence of mathematical content. In the third mode, the teacher is expected to “demonstrate, explain, and define the material, presenting it in an expository style” (Thompson, 1992, p. 136), and to be successful, students must demonstrate their knowledge of and proficiency with mathematical rules and algorithms. The classroom-focused model is not based upon any particular learning theory, but rather on the notion that students learn best when lessons are well structured and organized.
Based on multiple observations of each teacher and on teacher interviews prior to the professional development experience described in this study, the third mode, with its emphasis on performance, was by far the most dominant mode of instruction. The primary goal of the professional development was to help teachers transform their practice to a learner-focused model.
Use of Technology in Teaching
The NCTM and the Association of Mathematics Teacher Educators (AMTE) have called for mathematics teachers to use technology to support their instruction, enhance student learning, foster mathematical discourse, and facilitate discovery and conceptual understanding (NCTM, 2000; AMTE, 2008). AMTE (2009) further stated that for teachers to use technology effectively they must have a vast understanding of the content and connections that exist within the content, a rich and thorough understanding of how students learn mathematics, and a pedagogical base that encompasses the use of technology in their instruction. This view influenced us most in assisting the teachers in integrating technology into their instruction.
Burrill and colleagues (2002) performed a meta-analysis of research articles concerning the relationships between teacher beliefs about technology and about mathematics and mathematics education. Their work revealed a positive relationship between teachers’ beliefs about mathematics and their beliefs about the use of handheld graphing technology. For example, teachers with non-rule-based beliefs about mathematics viewed technology as integral to their instruction and were more likely to allow students more freedom in the way they chose to use the technology.
Teachers who had rule-based beliefs about mathematics were less likely to view technology as a means of improving or enhancing their instruction, focused on students’ affective reactions to calculator use, and were more likely to control the ways students used the technology (Burrill et al., 2002).
In their review of the literature related to teachers’ beliefs about technology integration, Zbiek and Hollebrands (2008) categorized teachers’ beliefs into three types: personal concerns, management concerns, and technology concerns. Teachers’ personal concerns deal with logistics, planning, and control and are related to how teachers view themselves as content experts and authorities in the classroom.
Management concerns relate to classroom management issues and the student learning that does or does not occur as a result. Teachers who have a rule-based approach to teaching mathematics have a structured approach to classroom management and to integrating graphing calculators into their instruction (Tharp, Fitzsimmons, & Ayers, 1997). These teachers tend to view the calculator as a computational tool, use it as such, and fail to acknowledge the ways in which the tool can be used to help students explore topics. The technology promotes structure rather than learning.
Technology concerns are identified as those relating to using the technology effectively during instruction. Taken together, these concerns related to broadening beliefs about using technology in the classroom initially present a challenge. These concerns were integral to our professional development efforts during our initial efforts to help teachers incorporate technology into their instruction. Other classifications of technology use (e.g., Beaudin & Bowers, 1997) influenced our thinking but did not have as profound an influence upon our design and data collection.
Zbiek and Hollebrands’ (2008) review of the research related to technology use indicated that “the ways in which technology is integrated into teachers’ classrooms is influenced by their conceptions of technology, mathematics, learning, and teaching.” Consequently, in designing our professional development, we paid close attention to teachers’ conceptions and made conscious efforts to perturb the teachers in ways that would help them experience the power of technology to deepen learning.
Chen (2008) found that in many cases a disconnect exists between teachers’ beliefs and practice. Chen cited three reasons for this disconnect: external factors such as administrative support, teachers’ conflicting beliefs, and teachers’ incomplete theoretical frameworks concerning teaching mathematics with technology. For our project, we had full support and encouragement from the administration, we worked to confront and influence teachers’ beliefs, and we discussed and provided experiences that were intended to aid them in infusing technology into their practice.
Further, there is a relationship between teachers’ beliefs about the effective use of technology and their beliefs’ about how mathematics should be taught. Turner and Chauvot (1995) suggested that teachers who view themselves as the content authority in the classroom believe students must completely understand mathematical procedures and concepts before being allowed to use technology. Nevertheless, other research has demonstrated that when teachers have opportunities to use a new technology as learners their conceptions of technology are broadened and their beliefs about technology integration expand (Drier, 2001). Consequently, we posited that supporting teachers and providing them with opportunities to use technology as learners would positively impact their instructional practice.
Technological Pedagogical Content Knowledge
Technology can be a useful tool for facilitating inquiry-based mathematics instruction, and through experience learning with technology teachers can gain knowledge and insight into using technology in their teaching. Scholars in the field of education developed a description of the knowledge required by teachers to incorporate technology effectively into their instruction, calling it technological pedagogical content knowledge (e.g., see Koehler & Mishra, 2005; the concept is often more recently referred to as technology, pedagogy, and content knowledge or TPACK). Technological pedagogical content knowledge consists of (a) the knowledge of teaching content with technology, (b) the knowledge of instructional decisions and representations for teaching content with technology, (c) and the knowledge of students’ learning with technology (Niess, 2008).
Grandgenett (2008) recommended that teacher education programs should integrate technology, content, and pedagogy within their coursework, prepare teachers to gain a disposition to experiment with new technologies, and offer teaching methods and mathematics content courses supporting the development of TPACK. This framework guided our work with teachers and, specifically, the questions we asked about the ways in which the professional development for the mathematics teachers should unfold.
Methods
Setting
The interventions and study were conducted at a middle school in a relatively small (approximately 27,000) urban district. Two middle schools were involved in the first year of the study, focusing on inquiry-based instruction in mathematics. Only one school was selected for adding the technological component for the second year. This was conscious decision was made primarily due to limitation of resources. The school that was selected for the technological component had designated itself a School of Inquiry and Innovation. The school had an enrollment of just under 600, with 54% White, 32% African American, 8% Hispanic, and 5% mixed race; 61% on free lunch and 8% on reduced lunch; and 15% classified as having special needs.
Participants
During the first year of the study, 4 of 6 mathematics teachers from the school participated in the Inquiry in Motion effort. During the second year, all 6 mathematics teachers participated. The two mathematics teachers who joined the effort the second year had prior commitments during the first year of the study; they had expressed an interest but were unable to participate.
Of the 6 teachers, all were female with a minimum of 3 years of experience. Five were elementary certified and had been grandfathered in by the South Carolina State Department of Education to obtain their middle school certificate; the other was originally certified to teach secondary mathematics. As such, though the teacher with the secondary background had extensive course work in mathematics, none of the teachers had special training or preparation for teaching middle school mathematics. Teacher information is provided in Table 1.
Table 1
Participating Teachers
Teacher Name | Grade Level Taught | Participated in Year 1 of Project | Initial Certification Type |
| Abby | 6th | Yes | Elementary |
| Beth | 6th | Yes | Elementary |
| Candice | 7th | No | Elementary |
| Debra | 7th | Yes | Elementary |
| Edith | 8th | Yes | Secondary |
| Frances | 8th | No | Elementary |
Data Sources
During the first year, data were collected from field notes, observations using the Electronic Quality of Inquiry Protocol, also known as EQUIP (Marshall et al., 2010), analyses of lesson plans, and interviews. During the second year, data were collected from field notes, interviews, surveys that were conducted at the middle and end of the year, and journals that teachers were required to keep. Teachers’ beliefs about the integration of technology into their instruction and their beliefs about how students learn were also assessed using a beliefs survey.
We included a teacher survey called Teacher Beliefs: Integrating Graphing Calculators into the Curriculum (see Appendix A), which included both Likert-style and open-ended questions. The researchers designed the teacher beliefs survey by adapting statements from two existing surveys on teacher attitudes toward integrating technology into the curriculum in a more general sense. We utilized the Survey of Factors Affecting Teachers Teaching with Technology (Papanastasiou & Angeli, 2008) and the Intrapersonal Technology Integration Scale (Neiderhauser & Perkmen, 2008). Internal consistency reliabilities for factors on the Survey of Factors Affecting Teachers Teaching with Technology ranged from 0.59 to 0.90. Overall reported internal consistency reliability on the Intrapersonal Technology Integration Scale was 0.96.
Professional Development
Each year of the project consisted of an 8-day summer institute (approximately 60 hours), four 2.5-hour follow-up sessions during the school year, and multiple one-on-one classroom visits and meetings with the classroom teachers by members of the professional development staff. The activities of the first year were focused on developing inquiry-teaching approaches within teachers’ practice.
In the second year we continued this work, but with a strong focus on the integration of technology. While Koehler and Mishra (2009) pointed out that considering components of knowledge in isolation can represent a disservice to good teaching, we posited that focusing on teachers’ pedagogical content knowledge, specifically teachers’ emerging understanding of the process of inquiry and key underlying concepts in middle school mathematics before introducing technology, provided teachers a foundation upon which to build.
Had the teachers all possessed sufficient background in content, we may have decided to develop inquiry contemporaneously with technology. However, we questioned whether merging content, inquiry, and technology at the same time would be overwhelming. Having 2 teachers join us in the second year of the project enabled us to study the question of whether we had made a sound decision.
First Year Intervention. Intervention activities of the first year were intentionally structured to address and deepen teachers’ current understanding of particular mathematical topics within their curriculum. Our initial goal was to perturb the teachers and to challenge their beliefs about mathematics, their content knowledge, and their practices. To do so, we spent the opening days of the professional development program having the teachers solve three middle grades level mathematics problems, for which the participants needed to explain their thinking and their solutions.
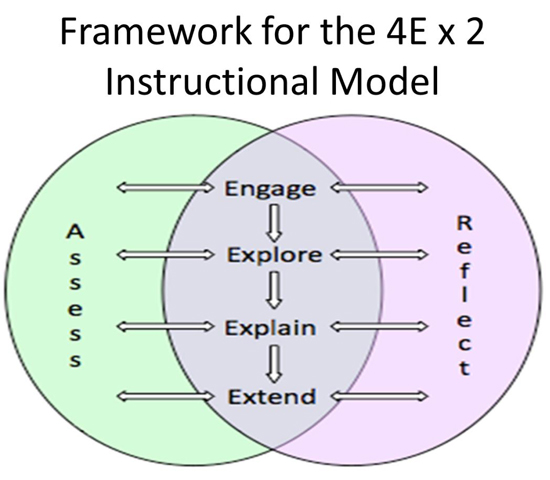
Each of the problems addressed multiple standards, though targeted on one of the big ideas in the middle school standards. One problem focused on number sense and operations, one on proportional reasoning, and one on data analysis. After each of the problems, we led a discussion unpacking the underlying mathematics, as well as the lesson structure used in working with the teachers. We also discussed the degree to which that structure might be effectively employed with their students. The structure for inquiry that we incorporated was the 4E X 2 (read “4E by 2; Marshall et al., 2009).
The 4E X 2 is a modification of the BCSC 5E Instructional Model (Bybee et al., 2006). Engage, explore, explain, and extend represent the “four Es.” Assessment and reflection, which should happen continually throughout the lesson, comprise the “by two.” The creators of this model described the 4E X 2 Instructional Model as
…a model for learning that links strong conceptual understanding of content with inquiry learning experiences. The 4E X 2 Model integrates what we know and understand about inquiry-based teaching and learning with effective assessment and metacognitive reflection. These three constructs, formative assessment, inquiry instructional models, and metacognitive reflection, are foundational to the Model. (Marshall et al., 2009, p. 501)
See Appendix B for a diagram representing the interactions of metacognitive reflection, inquiry instructional models and formative assessment.
Engaging the learner through an opening activity or task not only addresses motivation for learning, but may also serve to identify misconceptions, activate prior knowledge, or preassess prior knowledge as well. The purpose of explore-focused activities is to give student opportunity to engage in the development of mathematical ideas and to discover mathematical concepts, procedures, relationships, and so forth, along the way. This goal can be achieved with well-designed tasks and careful planning.
Explain-focused activities are connected to an explore activity. It is a lesson phase in which the teacher orchestrates a mathematical discussion to help students see the larger mathematical ideas embedded in the tasks they have worked on. Many times the explain activity is a discussion of the explore activity that preceded it.
Extend-focused activities are often other explore-focused activity or tasks designed to build on previously addressed mathematical knowledge. These tasks may further the mathematical content by involving applications, generalizations, or proof.
Having introduced and unpacked this model with the teachers, we next asked them to adapt lessons they had previously taught, restructuring them to fit the 4E X 2. The primary goal for adapting these was for the teachers to provide adequate opportunities, with proper scaffolding, for the students to explore the ideas prior to any explanation. Then, teachers began working in grade-level teams, first determining the big ideas for their particular grade and then developing lessons that addressed these big ideas.
In addition to the support of the project leaders, teachers were introduced to a web tool housed on the Inquiry in Motion website, which they would use for their lesson planning. The web tool supported their planning by providing lesson plan structure and guiding questions to ensure teachers had considered and addressed important elements of their inquiry lesson. The tool also served as a vehicle for collaboration and a location for posting and referencing multiple resources.
By the conclusion of the two-week summer session, teachers had posted on the site two inquiry-based lessons that they would implement in the first part of the year.
Throughout the first year, two members of the professional development team spent, on average, a total of 2 days per week visiting the 6 math teachers. Approximately one third of this time was spent conducting EQUIP observations, with the remaining time spent providing requested support. The most common form of support was to teach model lessons, but the support also included targeting specific EQUIP indicators, coteaching, and planning lessons.
Second Year Intervention. The second year of the project focused on integrating technology, namely a color-graphing calculator with natural display, and examining teachers’ existing and developing technological pedagogical content knowledge. We chose to focus on the graphing calculator because it is a piece of technology ubiquitous to schools. The Casio PRIZM was selected because we knew it was powerful and easy to use. PRIZM calculators and the related emulators were provided to every teacher along with sufficient calculators so that every student in the school would have access. Students in sixth and seventh grades had access to class sets, while students in eighth grade were provided individual calculators that they could take home and use throughout the year. (Casio America donated the calculators and software but played no role in the research, nor did project personnel receive any compensation from the company.)
The design of the professional development in this year was aligned with the current research that considers teachers’ technological pedagogical content knowledge. Specifically, teachers were simultaneously introduced to the basic functions of the calculators and how to use them to promote inquiry in mathematics. This manner of introduction forced teachers to further consider their core beliefs about teaching, as they needed to consider two questions: “How do I use this tool?” and “How might I use this tool to promote learning?” In other words, the introduction of technology use was not separated from the curriculum or the expected teaching practices. As mentioned, 2 of the 6 mathematics teachers joined the project in the second year, enabling us to investigate the third research question.
Prior to the second year, teachers’ beliefs regarding the integration of technology into their instruction and their beliefs about how students learn were assessed. We recognized the knowledge and beliefs of teachers acted as a filter through which they learned about effective technology integration to promote conceptual understanding. Professional development experiences throughout the project were designed to help teachers transform their beliefs about teaching mathematics with a graphing calculator, to encourage teachers to shift from procedural-based approaches, and to foster inquiry and exploration in their classrooms.
Transforming beliefs required teachers to consider more fully their current conceptions regarding teaching mathematics, the depth of their content knowledge, their beliefs about using technology in the classroom, the extent to which their beliefs had an impact upon their practice, and their self-efficacy in infusing the calculators into their instruction.
While we conceptualize our first year work as focused on pedagogical content knowledge (Shulman, 1986), the second year broadened our focus to technological pedagogical content knowledge. Of our 6 participants, only 1 had any prior experience using the graphing calculator, and her use had been mainly of an instrumentalist nature.
Despite the addition of the new participants in the second year, we continued our approach of perturbing teachers’ beliefs about mathematics, their content knowledge, and their practices; however, in each of our sessions in the second year, we did so through the use of the graphing calculator.
After a short (approximately 20-minute) initial period with the calculators, in which we had teachers learn how to perform basic skills with the calculator (such as turning it on and off and performing arithmetic), we presented a problem for the teachers to investigate. The participants from the first year worked alongside and assisted the new participants with the inquiry-based nature of the presented mathematics.
As a resource, we introduced a draft of a book written by one of the project leaders, Fostering Mathematical Thinking in the Middle School (Horton, 2012). This book contains dozens of classroom investigations with detailed explanations of possible solutions and discussion of salient mathematical, pedagogical, and technological concepts and skills. The book is based on the NCTM (2000) Principles and Standards for School Mathematics and was also informed by the initial draft of the Common Core Standards. The book presents challenging contextual problems for students to explore, think about mathematically, derive and justify solutions, and represent in multiple ways.
During the academic year, we held four face-to-face visits with all of the participants. Two project leaders, one of whom was a professor and the other an instructor pursuing her doctorate in curriculum and instruction with a focus on mathematics, each spent approximately 1 day per week at the school, providing support to the teachers as they requested. For some of these occasions, the leaders cotaught with the teachers, For others, the project leaders taught the class while the teachers observed, and at other times the leaders observed, using the EQUIP protocol to assess the quality of inquiry in the classroom. Most sessions were followed by a debriefing session, when teachers’ schedules allowed.
Although the teachers selected the form this support would take and could make specific requests, the leaders kept track of the number of visits to ensure that project support was balanced approximately equally among the teachers.
The charge to the teachers for the school year was to use the calculators regularly, complete at least two major investigations from the Horton (2012) book each quarter, keep a journal in which they documented significant events, feelings, thoughts, and experiences, communicate regularly with the project leaders, provide access to their classrooms for visits, complete the midyear and year-end surveys, and focus their instruction on exploration before explanation when teaching big ideas. This last charge was also the major emphasis of the first year.
Results
The EQUIP scale provides a guide for assessing a teacher’s level of inquiry on four main facets of instruction: instructional factors, discourse factors, assessment factors and curriculum factors. Each of the four facets is assessed in 5-minute intervals throughout a lesson. At the conclusion of a lesson, a teacher is given a composite score for each of the four facets (from 1-4, associated with a level of inquiry). These composite scores are then combined to create an overall lesson score. Prior to the first year of the project intervention, all teachers’ lessons received an overall score of 1 (Pre-Inquiry) on the EQUIP scale. The category of Pre-Inquiry reflects a largely didactic pedagogical approach in which explanations of content precede students’ engagement or investigation. By the end of the first year, 5 of the 6 teachers’ lessons had progressed to an overall score of 2 (Developing Inquiry) on the EQUIP scale. Developing Inquiry is characterized by instruction that allows students to explore content prior to explanations built from the teacher’s understandings.
In Proficient Inquiry (an EQUIP score of 3) explorations are followed by explanations orchestrated by the teacher using students’ understandings. Although we fell short of our target of Proficient Inquiry, we recognized this transformation to inquiry would take considerable time, and the trajectory and teachers’ desire to incorporate inquiry more fully suggested we were moving in the right direction.
Research Question 1
In order to answer our research question regarding the participants’ initial beliefs toward the incorporation of calculators into their teaching, we administered a beliefs survey at the beginning of Year 2, consisting of 25, 5-point Likert-scale items and four open-ended response items (Appendix A). The survey was administered in July 2011, after the six participants had had a brief exposure to the graphing calculators, but had not yet conducted any full investigation. Results for the Likert-scale items have been reverse-coded as appropriate so a higher score represents a more positive view toward incorporating graphing calculators. Each teacher’s number of response types on the Likert scale is represented in Figure 1. Five of 6 participants initially exhibited positive attitudes toward incorporating of graphing calculators, as evidenced by the high proportion (50+%) of responses of agree (4) or completely agree (5). Frances had the majority of her responses as neutral (3) or lower. Edith was the teacher with some prior work with a graphing calculator, though not the brand type we were using in our intervention.
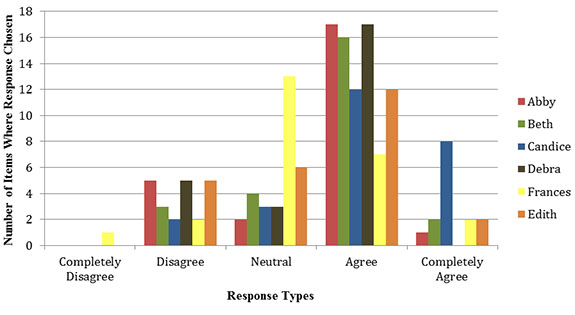 Figure 1.Total initial response types on the beliefs survey.
Figure 1.Total initial response types on the beliefs survey.
Despite the positive responses on the surveys, our field notes captured teachers’ apprehension related to the integration of the calculators. Following are representative comments from the four open-ended survey questions, showing both teachers’ enthusiasm for and apprehensions about the project (Table 2). We have included the participant’s name in cases where we could clearly identify her.
Table 2
Example Teacher Comments About Incorporating Calculators Into Mathematics Instruction
Themes | Teachers’ Comments |
| Technical Issues Related to the Calculator |
|
| Conceptual or Mathematical Issues Related to the Calculator |
|
| Curricular or Implementation Issues Related to the Calculator |
|
During the third year of the project, Edith and Frances moved to work at other schools in the district. Debra had indicated that she no longer wished to fully participate in the project. We purposefully focused more in depth on Candice, Abby, and Beth. Both Abby and Beth had participated in the project since its inception, and Candice joined the project during its second year, when the graphing calculators were introduced.
This stragegy allowed us to consider the ways in which these teachers responded to the introduction of inquiry-based instruction and technology in different ways. We looked at the number of survey responses from these teachers receiving a score of 1, 2, 3, 4, or 5 (see Figure 2). All three teachers tended to demonstrate positive beliefs about technology integration.
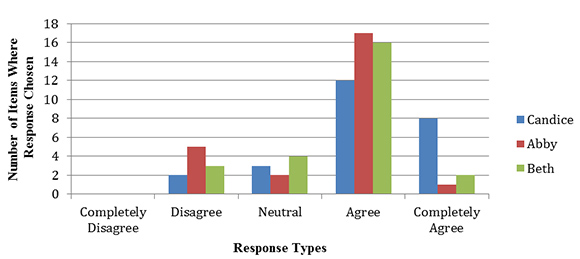 Figure 2. Total initial response types of Candice, Abby, and Beth on the beliefs survey.
Figure 2. Total initial response types of Candice, Abby, and Beth on the beliefs survey.
Perhaps most noteworthy, Candice did not participate in the project during its first year and had not been introduced to inquiry-based instruction prior to being introduced to the graphing calculator. She responded to eight questions on the survey with a strongly agree, further demonstrating her interest and willingness to teach with technology.
Research Question 2
The analysis of the Teacher Belief surveys from the beginning of Year 2 (initial introduction to the graphing calculator) to the beginning of Year 3 revealed a positive shift in beliefs for each teacher involved in the project (see Table 3). Responses from all 6 teachers indicated that over their course of involvement with the project, beliefs expanded to encompass the idea that graphing calculators can be used to support and encourage inquiry in mathematics and that the graphing calculator can be used to help students understand mathematical concepts more completely.
Table 3
Overall Mean Scores for All Six Teachers
Teacher Name | Overall Mean Score (July 2011) | Overall Mean Score (Sept. 2012) | Overall Mean Score Difference |
| Abby | 3.56 | 4.16 | 0.6 |
| Beth | 3.68 | 4.44 | 0.76 |
| Candice | 4.04 | 4.44 | 0.4 |
| Debra | 3.48 | 4.24 | 0.76 |
| Edith | 3.44 | 4.28 (May 2012) | 0.84 |
| Frances | 3.28 | 3.48 (May 2012) | 0.2 |
Because of the small sample size, we did not run hypothesis tests nor compute confidence intervals. We determined, albeit arbitrarily, a change of 0.75 or more, merited further investigation. The following survey statements had an increase in mean of at least 0.75:
- The graphing calculator changes the way students learn in my classes.
- The graphing calculator can help students understand concepts in more effectively than traditional instruction.
- I feel confident that I can teach significan math content with appropriate use of the graphing calculator.
- I feel confident that I have the necessary skills to se the graphing calculator for instruction.
- I feel confident that I can regularly incorporate the graphing calculator into my lessons to enhance student learning.
These results demonstrate that after their initial semester of usage, the teachers grew in several key areas during the second semester of implementation. Among other things, this finding supports the need for patience when important and significant changes are expected.
We again chose to focus more in depth on three teachers for our data analysis: Abby, Beth, and Candice. Candice was an award-winning teacher, but one who viewed middle school mathematics from an instrumentalist, arithmetic approach. Based on our observations and field notes, Candice largely employed direct instruction in her classroom and focused on having students memorize specific rules and procedures, with little explanation as to why they were important or worked.
Between the midyear 2011 and end-of-year 2012 surveys, the number of statements with a positive change of at least 1 point on the Teacher Beliefs Survey included the following: Abby, 11; Beth, 13; and Candice 6. Table 4 lists a sample of the specific survey questions that showed this change.
Table 4
Sample Statements on Beliefs Survey That Show Positive Changes
Teacher Name | Statements |
| Abby |
|
| Beth |
|
| Candice |
|
Though Candice’s beliefs about teaching with the graphing calculator, as evidenced in the survey, had not shifted as much as Beth’s and Abby’s, her comments from an interview, along with several one-on-one support sessions, indicated that her ideas about teaching inquiry-based mathematics with the graphing calculator had, in fact, changed significantly.
Before the project, she was confident that she was doing an excellent job in teaching mathematics; however, the project perturbed her and, in time, convinced her that she was not leading her students to deep understanding of mathematical ideas, nor was she requiring them to think at the depths she had now come to expect.
At the end of the first semester of the second year, though participants continued to voice some concerns, they were even more positive than they had been initially. By the end of the second year, the data reflect a consistently positive outlook about the use of the calculators in the classroom. The greatest change in mean scores occurred for the following questions:
16. The technical support for integrating the graphing calculator in my school is adequate.
17. The instructional support for integrating the graphing calculator in my school is adequate.
Teachers believed that they had adequate support in fully integrating the technology, were excited about using technology, and did not view the technology as presenting technical problems in their classrooms.
We also analyzed the overall mean scores for the three teachers of interest. As Figure 3 and Table 5 illustrate, all three teachers demonstrated an overall increase in their beliefs about effective incorporation of the graphing calculator into their instruction.
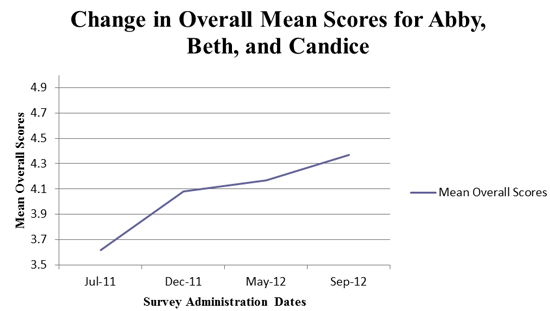
Figure 3. Change in overall mean scores for Abby, Beth, and Candice.
Table 5
Overall Mean Scores for Abby, Beth, and Candice
Teacher Name | Overall MeanScore (July 2011) | Overall MeanScore (Sept. 2012) | Overall Mean Score Difference |
| Abby | 3.56 | 4.16 | 0.6 |
| Beth | 3.68 | 4.44 | 0.76 |
| Candice | 4.04 | 4.44 | 0.4 |
Candice’s initial scores on the survey were more positive than that of Abby and Beth. Also, Abby’s overall mean scores on the beliefs survey showed a slight decrease from the end of Year 2 to the beginning of Year 3 (4.36 to 4.16). Perhaps this change was due to her concerns that she may have forgotten much of what she had learned during the previous year.
Also of interest is the overall mean score difference for the three teachers. While Candice showed an increase of 0.4 in responses, Abby and Beth demonstrated even more change overall. The explanation may be that Abby and Beth were introduced to inquiry-based instruction prior to being introduced to the graphing calculator as a teaching and learning tool and, consequently, were not cognitively overloaded with the inclusion of the calculator.
Candice, on the other hand, was coping with a move toward content-embedded inquiry along with the inclusion of the graphing calculator. However, she did show a significant increase over the summer when she had the opportunity to reflect upon the previous year and then participated in the summer professional development. She also indicated that she did significant work on her own during the summer, which could also have contributed to this increase.
None of the teachers met all of the expectations expressed to them prior to the start of Year 2. Specifically, none conducted two major technology-rich, inquiry-based investigations each quarter. From interviews, we determined that this was not due to concerns about the technology but, instead, concerns about the inquiry. Without exception, they indicated that neither they nor their students were prepared to engage in explorations that would take more than one class period. While they all shifted to having students explore ideas before an explanation, they were still working on transforming their practice so as to engage in deeper mathematical explanations.
Research Question 3
To address the third research question, in addition to studying the survey results and our field notes, we interviewed the three teachers of interest: Candice, Abby, and Beth.
The school administrators considered all three of these teachers to be outstanding. Both Abby and Beth had been elementary education majors, with Abby having taught 12 years and Beth having taught 3 years prior to the start of the program. As evidenced by their interviews, they found the transformation to an inquiry-based model of instruction challenging and believed that they would have been overwhelmed had they been expected to learn how to use graphing calculators at the same time they were expected to transform their primary method of instruction.
I believe that if I would have to have done the calculators and the inquiry learning at the same, in the same year, it would have been a little overwhelming. The only way I feel like that would have worked is if I would have had knowledge about calculators prior, like when, when you introduce the calculator, I was learning it for the first time. So, I had to learn how to use the calculator, plus keep in mind everything with inquiry. Had I known anything about the calculator, I might have handled both of them in one year. But, would it be new? I definitely feel like the two different years was very important. Because, I mean, to me, just learning inquiry was a big deal. I mean, learning, you know, the 4Es, that was, that was a big deal to me.…I needed the foundation of what inquiry was, how it was going to transform my classroom, and what I needed to do as far as helping the students learn to discover the math themselves. So, that was like a whole task within itself that, that I think the whole year, really helped me focus on that before I added the calculators. (Abby, interview)
I’d say I do think that the first year of having my foundation of inquiry helped a good bit. It just helped kind of shift my classroom focus over, and then, I do think that that made implementing in the calculators and the technology much easier, because I felt like I’ve already had an inquiry-based classroom. Then, I can implement the calculators and use them as a tool for inquiry, but I did not have to shift all at once. (Beth, interview)
Another important finding is that the process of changing their primary method of instruction to one of inquiry enabled all teachers to recognize and address gaps in their content knowledge, especially in their conceptual understanding of procedures they were comfortable in using and teaching. Proportion was one such example. Initially, teachers’ understanding of proportions was particularly weak and relegated to the rote process of setting up and solving proportions using cross-multiplying and dividing.
Through exploring with the calculators however, they began to develop a more conceptual view of proportions and made connections between proportions and other mathematical topics. Specifically, the teachers discovered that a proportional relationship between two variables was linear, and its solution set always contained the origin. A similar development of understanding and connections occurred when exploring decimal representations of rational numbers.
The teachers used technology to gather data of repeating and terminating decimal representations of fractions. In connecting their observational data to their knowledge of number theory, teachers were able to generalize a rule stating that a given fraction would have a repeating decimal representation if and only if the denominator of the fraction in simplest form contained any prime factors other than 2 or 5.
In the middle of her first year of participation, Candice said, “I was very skeptical at first. I am no longer skeptical, however; I have realized I have so much to learn. This is stretching me with my beliefs and deepening my content knowledge.”
By the end of her second year in the project, the process of change had clearly influenced Beth’s view of her own teaching and knowledge, as well: “I feel like my teaching has drastically changed since we began two years ago: a lot more inquiry and technology. My content knowledge has really improved.”
Candice provided a fascinating contrast to both Beth and Abby. Candice had 12 years of teaching experience prior to her involvement with the project, 6 of which were in math, and had degrees in elementary education and a master’s degree in elementary school leadership. Several times during the interview she indicated that she had wished she had been able to participate during the first year, positing that it would have helped her to manage all of the expectations she had for herself in making changes to her practice.
I definitely think it impacted me because it was so overwhelming to have to try to do both pieces at one time. And it was not quite the seamless transition I would have liked it to be. It’s almost like when I focused on one piece of it and I let the other piece slide or vice versa, so I wish I would have had more of the inquiry background before the calculator started. I did have some because [Abby and Beth] were good to share with me, but it was just not the same as actually having been there. (Candice, interview)
Candice had spoken with the other project teachers about their experiences with inquiry, but claimed these conversations, though interesting, were not sufficient to motivate her to modify her instruction. It was, in fact, the calculators and the opportunities they presented that convinced her she needed to change from what she had believed was an appropriate and effective method for teaching mathematics.
I tried to use the calculator as an inquiry tool and wasn’t really prepared fully as far as the inquiry piece goes. I feel like that was where my, you know, my weakness was, how to use the tool best for the inquiry. And I wish I would have taken baby steps instead of one big jump into all of it. I can see, you know, separating it out, how that would work, but I also see how I wasn’t fully convinced until I saw all of it merged together. (Candice, interview)
As a result of her work in the project, she became convinced that changes to technology enriched, inquiry-based instruction could and probably should happen contemporaneously. Further, Candice’s experiences in the project helped to make the act of teaching problematic, and they encouraged her to keep working on her practice.
Discussion
The change to a technology-rich, inquiry-based approach has been, as expected, time consuming and has required significant supports. Teachers, though, have been positive about the change. Once they were perturbed sufficiently to challenge their perspectives concerning the meaning of mathematics and the goals of middle school mathematics, all of the teachers in the project embraced the transition.
Their transformation was significantly complicated by their past successes in a direct instruction, skill-based model and the doubts they had pertaining to the depths of their own knowledge and skills. Though we have not reported on the changes in practice in this article, those changes have lagged, as all of the teachers in the project have readily admitted. Nevertheless, as support has continued, even with a positive perspective from the onset, their views have continued to become more positive.
The teachers have embraced color-graphing calculators as exploratory tools that can foster mathematical thinking. However, even after a full year of support in integrating technology, though more confident, the teachers have requested more professional development, sample and team teaching episodes, and support in breaking down investigations into manageable components. Thus, we are continuing to work with these teachers for a third year.
Candice, the teacher who was introduced to inquiry-based instruction and the graphing calculator as a tool to facilitate inquiry-based instruction at the same time, was quick to embrace the changes and found the graphing calculator to be the catalyst to motivate her to make these changes. She was, and continues to be, vocal about requesting classroom support, particularly asking project leaders to teach lessons so she can take notes and then model her instruction after ours. Though, as she readily admits, changes are still needed, Candice fully accepted the integration of the calculator into inquiry-based instruction. She did not recognize a need to separate the technological goals from the broader pedagogical changes, although she admitted that at times she felt overwhelmed.
Abby and Beth, who experienced a year of professional development focused on inquiry-based instruction prior to their focus on calculator usage, have also been mostly successful in their transformation, though both said they still have much room for growth and have also requested continued support. They remain convinced, however, that they would have been overwhelmed had the technology been introduced during the first year.
Another teacher who participated in both years, Debra, on the other hand, did not make many changes. Though her beliefs about mathematics were modified slightly, her primary concern was her students’ performance on the high-stakes, end-of-year state test. Because students were not allowed to use a calculator on the test, she thought the students would not be adequately prepared. This belief was transferred to her students as well. For this group, the calculator was not a learning tool, but merely a device to get results quickly and accurately.
In summary, then, the transformation is an individual process and, as Loucks-Horsley et al. (2003) have indicated, no single prescription fits all situations. Teachers come with different experiences and different backgrounds and can experience and interpret the same professional development in different ways. Technology can make a significant difference in how teachers approach mathematics, though we have conflicting evidence as to whether the technology should be introduced at the same time as an inquiry-based approach is introduced. For some, it may be too much, while for others the technology can provide the motivation to make such a major change.
We recognize our particular intervention and specific context limit the generalizability of our belief results. However, our project provides valuable evidence to consider in the design of future professional development projects attempting to address issues of technology and pedagogy.
Implications
Results support prior findings of the slow pace of transformation, but are nevertheless encouraging. Though there was a clear exception, the teachers now have a different conception of mathematics and are working to transform their instruction.
Personalized support, however, has been essential for these teachers, and requests for this support continue into the third year of the program. The feasibility of providing this type of professional development on a large scale, then, is problematic. Insufficient resources exist to support each school in the fashion described here. Consequently, our current and future efforts are geared toward institutionalizing the changes and supporting the changes without such an intense commitment of time and resources.
Coaching models have provided some ideas for these changes. If coaches are not available, then having a lead teacher who provides the support necessary for continued change may be possible. We are also investigating partnerships with the computer science department to develop and support remote learning/teaching/supporting opportunities. Applications may also exist that provide ready access to information, ideas, and teaching videos to provide the scaffolding and ongoing support that teachers need to implement such profound changes in their beliefs and practices.
As these teachers have demonstrated, change is possible and can be worthwhile. As their school principal said, because of the changes made by these teachers “students now are thinking at much deeper levels.”
References
Association of Mathematics Teacher Educators. (2006). Preparing teachers to use technology to enhance the learning of mathematics: A position of the Association of Mathematics Teacher Educators. Retrieved from http://www.amte.net/sites/all/themes/amte/resources/AMTETechnologyPositionStatement.pdf
Association of Mathematics Teacher Educators (AMTE). (2009). Mathematics TPACK framework. Retrieved from http://www.amte.net/sites/all/themes/amte/resources/MathTPACKFramework.pdf
Beaudin, M., & Bowers, D. (1997). Logistics for facilitating CAS instruction. In J. Berry, J. Monaghan, M. Kronfellner, & B. Kutzler (Eds.), The state of computer algebra in mathematics education (pp. 126-135). Lancashire, England: Chartwell-York.
Boaler, J. (1998). Open and closed mathematics: Student experiences and understandings. Journal for Research in Mathematics Education, 41-62.
Burrill, G., Allison, J., Breaux, G., Kastberg, S., Leatham, K., & Sanchez, W. (2002). Handheld graphing technology in secondary mathematics. Dallas, TX: Texas Instruments.
Bybee, R. W., Taylor, J. A., Gardner, A., Van Scotter, P. V., Carlson, J., Westbrook, A., & Landes, N. (2006). The BSCS 5E instructional model: Origins, effectiveness, and applications. Colorado Springs: BSCS.
Chen, C. (2008). Why do teachers not practice what they believe regarding technology integration? The Journal of Educational Research, 102(1), 65-75.
Common Core State Standards Initiative. (2010). Common core state standards for mathematics. Retrieved from http://www.corestandards.org/assets/CCSSI_Math%20Standards.pdf
Drier, H.S. (2001, March). Beliefs, experiences, and reflections that affect the development of techno-mathematical knowledge. Paper presented at the meeting of the Society for Information Technology and Teacher Education, Orlando, FL.
Ernest, P. (1988). The knowledge, beliefs, and attitudes of the mathematics teacher: A model. Unpublished manuscript, University of Exeter, England.
Fennema, E., & Franke, M. L. (1992). Teachers’ knowledge and its impact. In D. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 147-164). New York, NY: Macmillan.
Grandgenett, N. F. (2008). Perhaps a matter of imagination: TPCK in mathematics education. In J. Colbert, K. Boyd, K.Clark, S. Guan, J. Harris, M. Kelly, & A. Thompson (Eds.), Handbook of technological pedagogical content knowledge (TPCK) for educators (pp. 145-166). New York, NY: Routledge.
Haury, D. L. (2002). Learning science through design (ERIC Digest). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education.
Heid, M.K., & Blume, G. (Eds). (2008). A research-informed view of the process of incorporating mathematics technology into classroom practice by in-service and prospective teachers. In M. Zbiek, & K. Hollebrands (Eds.), Research on technology and the teaching and learning of mathematics (Vol. 1; pp. 287-344). Charlotte, NC: Information Age Publishing, Inc.
Horton, R. M., (2012). Fostering mathematical thinking in the middle grades. Dover, NJ: Casio America, Inc.
Killion, J., & Harrison, C. (2006). Taking the lead: New roles for teachers and school-based coaches. Oxford, OH: National Staff Development Council.
Koehler, M.J., & Mishra, P. (2009). What is technological pedagogical content knowledge? Contemporary Issues in Technology and Teacher Education, 9(1). Retrieved from https://citejournal.org/vol9/iss1/general/article1.cfm
Kuhs, T. M., & Ball, D. L. (1986). Approaches to teaching mathematics: Mapping the domains of knowledge, skills, and dispositions. East Lansing, MI: Michigan State University, Center on Teacher Education.
Lerman, S. (1990). Alternative perspectives of the nature of mathematics and their influence on the teaching of mathematics. British Educational Research Journal, 16(1), 53-61.
Loucks-Horsley, S., Love, N., Stiles, K., Mundry, S., & Hewson, P. (2003). Designing professional development for teachers of science and mathematics. Thousand Oaks, CA: Corwin Press, Inc.
Marshall, J. C., & Horton, R. M. (2011). The relationship of teacher facilitated inquiry-based instruction to student higher-order thinking. School Science and Mathematics, 111(3), 93-101.
Marshall, J. C., Horton, B., & Smart, J. (2009). 4E x 2 instructional model: Uniting three learning constructs to improve praxis in science and mathematics classrooms. Journal of Science Teacher Education, 20(6), 501-516.
Marshall, J. C., Smart, J., & Horton, R. M. (2010). The design and validation of EQUIP: An instrument to assess inquiry-based instruction. International Journal of Science and Mathematics Education, 8(2), 299-321.
National Council of Teachers of Mathematics. (1980). Agenda for action. Reston, VA: Author.
National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (1991). Professional standards for teaching mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
National Research Council. (1996). National science education standards. Washington, DC: National Academies Press.
Neiderhauser, D. S., & Perkmen, S. (2008). Validation of the intrapersonal technology integration scale: Assessing the influence of intrapersonal factors that influence technology integration. Computers in Schools, 25(1-2), 98-111.
Neufeld, B., & Roper, D. (2003). Coaching: A strategy for developing instructional capacity – promises and practicalities. Washington, DC: Aspen Institute Program on Education, and Providence, RI: Annenberg Institute for School Reform.
Niess, M. L. (2008). Guiding preservice teachers in developing TPCK. In N. Silverman (Ed.), Handbook of technological pedagogical content knowledge (TPCK) for educators. (pp. 223–250). New York, NY: Routledge.
Pajares, F. (1992). Teachers’ beliefs and educational research: Cleaning up a messy construct. Review of Educational Research, 62, 307-332.
Papanastasiou, E. C., & Angeli, C. (2008). Evaluating the use of ICT in education: Psychometric properties of the survey of factors affecting teachers teaching with technology (SFA-T3). Educational Technology & Society, 11 (1), 69-86.
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4-14.
Shymansky, J. A., Kyle, W. C., & Alport, J. M. (1983). The effects of new science curricula on student performance. Journal of Research in Science Teaching, 20(5), 387-404.
Tharp, M.L., Fitzsimmons, J.A., & Brown Ayers, R.L. (1997). Negotiating a technological shift: Teacher perception of the implementation of graphing calculators. Journal of Computers in Mathematics and Science Teaching, 16, 551-575.
Thompson, A.G. (1992). Teachers’ beliefs and conceptions: A synthesis of the research. In D. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 127-146). New York, NY: Macmillan.
Turner, P., & Chauvot, J. (1995). Teaching with technology: Two preservice teachers’ beliefs. In D. Owens, M. Reed, & G. Millsaps (Eds.), Proceedings of the 17th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 115-121). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education.
Wise, K. C., & Okey, J. R. (1983). A meta-analysis of the effects of various science teaching strategies on achievement. Journal of Research in Science Teaching, 20(5), 419-435.
Zbiek, R. M., & Hollebrands, K. (2008). A research-informed view of the process of incorporating mathematics technology into classroom practice by inservice and prospective teachers. Research on Technology and the Teaching and Learning of Mathematics, 1, 287-344.
Author Notes
Andrew M. Tyminski
Clemson University
Email: [email protected]
Leigh Haltiwanger
Clemson University
Email: [email protected]
V. Serbay Zambak
Clemson University
Email: [email protected]
Robert Horton
Clemson University
Email: [email protected]
Traci Hedetniemi
Clemson University
Email: [email protected]
Teacher Beliefs: Integrating Graphing Calculators into the Curriculum
Please circle the responses that best represents the extent of your agreement or disagreement with each statement.
Completely Disagree | Disagree | Neutral | Agree | Completely Agree | |
| 1. I feel comfortable with the idea of the graphing calculator as a tool in teaching and learning. | 1 | 2 | 3 | 4 | 5 |
| 2. The use of graphing calculators in teaching and learning stresses me out. | 1 | 2 | 3 | 4 | 5 |
3. The idea of using a graphing calculator in teaching and learning makes me skeptical. | 1 | 2 | 3 | 4 | 5 |
| 4. The use of the graphing calculator as a learning tool excites me. | 1 | 2 | 3 | 4 | 5 |
| 5. The use of the graphing calculator in teaching and learning scares me. | 1 | 2 | 3 | 4 | 5 |
| 6. The use of the graphing calculator changes the way I teach. | 1 | 2 | 3 | 4 | 5 |
| 7. The graphing calculator changes the way students learn in my classes. | 1 | 2 | 3 | 4 | 5 |
| 8. Students learn better from the teacher than they do by exploring with the calculator. | 1 | 2 | 3 | 4 | 5 |
| 9. The graphing calculator is not conducive to student learning because it is not easy to use. | 1 | 2 | 3 | 4 | 5 |
| 10. The graphing calculator can help students understand some concepts more effectively than traditional instruction. | 1 | 2 | 3 | 4 | 5 |
| 11. The graphing calculator can help students learn because it allows them to explore and discover ideas. | 1 | 2 | 3 | 4 | 5 |
| 12. The graphing calculator is not conducive to good teaching because it creates technical problems. | 1 | 2 | 3 | 4 | 5 |
Completely Disagree | Disagree | Neutral | Agree | Completely Agree | |
| 13. The principal encourages me to integrate the graphing calculator into my teaching. | 1 | 2 | 3 | 4 | 5 |
| 14. I exchange ideas about integrating the graphing calculator with other teachers. | 1 | 2 | 3 | 4 | 5 |
| 15. A variety of instructional resources for integrating the graphing calculator are available for use in my school. | 1 | 2 | 3 | 4 | 5 |
| 16. The technical support for integrating the graphing calculator in my school is adequate. | 1 | 2 | 3 | 4 | 5 |
| 17. The instructional support for integrating the graphing calculator in my school is adequate. | 1 | 2 | 3 | 4 | 5 |
| 18. I feel confident that I can teach significant math content effectively with appropriate use of the graphing calculator. | 1 | 2 | 3 | 4 | 5 |
| 19. I feel confident that I have the necessary skills to use the graphing calculator for instruction. | 1 | 2 | 3 | 4 | 5 |
| 20. Using the graphing calculator in the classroom is increasing my effectiveness as a teacher. | 1 | 2 | 3 | 4 | 5 |
| 21. I feel confident I can regularly incorporate the graphing calculator into my lessons to enhance student learning. | 1 | 2 | 3 | 4 | 5 |
| 22. I feel confident that I can help students when they have difficulty using the graphing calculator. | 1 | 2 | 3 | 4 | 5 |
| 23. Effectively using the graphing calculator in the classroom will increase my sense of accomplishment. | 1 | 2 | 3 | 4 | 5 |
| 24. Using the graphing calculator in the classroom is improving my teaching. | 1 | 2 | 3 | 4 | 5 |
| 25. I feel confident that I can effectively use the graphing calculator in my teaching. | 1 | 2 | 3 | 4 | 5 |
26. What has surprised you as you’ve begun to incorporate the graphing calculator into your instruction?
27. What are some of the challenges you face as you continue to find ways to use graphing calculators?
28. Describe how your attitudes and beliefs about using the graphing calculator to teach math have changed.
29. In order to more fully use the graphing calculator to teach math, what other supports do you need?
Appendix B
The 4Ex2 Instructional Model
![]()