Browning and Klespis (2001) raised a number of thoughtful and important issues in their reaction to our article concerning guidelines for the preparation of preservice secondary mathematics teachers (PSTs) to use technology appropriately in their teaching (Garofalo, Drier, Harper, Timmerman, & Shockey, 2000). In this reply, we provide examples of our work with PSTs and illustrations of actual work done by PSTs to address their two main points, namely that (a) preservice teachers need to experience the learning of ‘new’ mathematics with technology, and (b) preservice teachers usually struggle with appropriate use of technology as beginning teachers.
Experiencing Mathematics Topics Again, for the First Time
Most secondary mathematics teacher education programs require either a major or a strong concentration (e.g., 30 credits or more) in mathematics. At the University of Virginia, for example, PSTs are mathematics and education majors and are awarded both a BA in mathematics and an MT in education concurrently at the end of five years of study. Hence, they come into our mathematics pedagogy course in their fourth year having relatively strong mathematics backgrounds, including exposure to many advanced mathematics topics in a variety of areas. Despite this background, a number of PSTs come to us without knowledge of some topics that they will teach in secondary classrooms, such as recursion, regression, and fractals. Their learning of these topics, enhanced by technology, is very different from their learning of topics in both their high school and college mathematics courses. This allows them to reflect on various aspects of the experiences they have had learning these topics and to compare them to learning experiences they have had with other mathematics topics.
Even though PSTs come to us having completed eight or nine college mathematics courses, they often lack conceptual knowledge of some topics they have studied, including some at the secondary level. Too often, their knowledge of these topics can be characterized as procedural (Hiebert & Lefevre, 1986) or instrumental (Skemp, 1978). Skemp went so far as to say that instrumental mathematics (rules without reason) is different mathematics from relational mathematics (knowing what to do and why)!
When PSTs are learning these topics conceptually for the first time with technology, they often experience ‘Ah ha!’ or ‘Eureka!’ moments. These moments provide opportunities to discuss and compare methods of teaching and quality of learning. One example of such a topic is Taylor’s theorem. Most PSTs recall the theorem and are able to tell us that it is about approximating functions with series, and many remember the expansion formula and can generate terms. But rarely are PSTs able to conceptually or graphically explain the theorem. They are usually confused about points of expansion and the remainder terms. However, once they algebraically expand a function about a point, generate graphs and tables for several approximations, and analyze their results, they develop understandings that they never had. (Figure 1.)
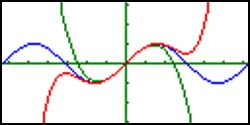
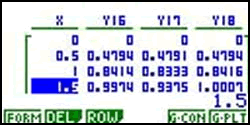
Figure 1 . Graphs and table of sin( X ) (blue), X – X 3 /3! (green), and X – X 3 /3!+ X 5 /5! (orange)
Another such topic is linear programming. All our PSTs remember that to find the extreme values of an objective function all one has to do is evaluate it at the intersection points of the graphs of the constraining functions defining the feasibility region. No PST has ever been able to explain to us why this works. However, once they explore the interactive linear programming applet at ExploreMath.com by dynamically observing values of the objective function as the cursor is moved over points in the feasibility region and interpreting and explaining what is happening, they begin to understand that they are evaluating a linear surface defined over a two-dimensional region. (Figure 2.) The Linear Programming applet, requiring a Shockwave plug-in, can be found at http://www.exploremath.com/activities/Activity_page.cfm?ActivityID=31 .
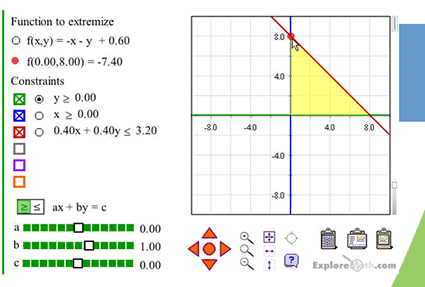
Figure 2. The ExploreMath.com Linear Programming applet
We believe, following Skemp, that in a very real sense, PSTs are learning new mathematics in each of these instances. Furthermore, they are in a position to reflect on differences between their ‘old’ learning and their ‘new’ learning and connect them to differences in teaching approaches.
Learning to Teach with Technology
The other point Browning and Klespis made is that it takes time to learn how to incorporate technology appropriately into one’s teaching. We wholeheartedly agree. We believe that the approach we take, characterized by the guidelines discussed in our previous article, helps PSTs begin to learn how to use technology in their subsequent teaching. Not only are they learning features of various technologies, but they are experiencing some of the potential benefits afforded by appropriate use of technology in a classroom where using technology as a teaching and learning tool is explicitly modeled and discussed. We have not yet conducted formal research on the impact of these experiences on our PSTs, but we do have examples of PSTs’ use of technology to enhance teaching. The following six examples illustrate a variety of ways that our PSTs have used their learning experiences with technology as building blocks to develop lessons and tools they believe embody appropriate use of technology in a mathematics classroom.
Mitch’s Linear Programming Lesson . When Mitch was a student teacher introducing the concept of linear programming to his students in an Algebra II class, he proposed the following situation:
You are organizing the items to be sold at the concession stand for the next home football game. You notice that you have 2,500 cups that are used for both hot chocolate and coffee. Hot chocolate sells for 50 cents while coffee sells for 30 cents. If you must sell at least 300 cups of hot chocolate and 500 cups of coffee, how many cups of each must you sell in order to maximize your profit?
After his students generated the constraint functions from the given information and graphed them on their calculators, they interpreted the area bounded by these three constraints as a planar region that represents the possible solution set. The students knew that they needed to evaluate the profit function at the intersections of y = 2,500 ‘ x and y = 500 and of y = 2,500 ‘ x and x = 300, and were able to find them with their calculators (Figure 3).
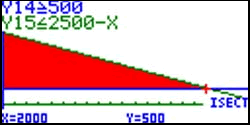
Figure 3 . The intersection of y = 2,500 ‘ x at y = 500
Mitch was not satisfied with his students merely knowing how to determine the maximum values of the profit function procedurally, as he did prior to working with the ExploreMath applet (Figure 2). He wanted them to understand why the method they used was mathematically justified. He did not have access to ExploreMath in his classroom, so he had to improvise. To assist his students in seeing that the maximum value of the profit function, a three-dimensional surface, occurred at a vertex of the feasibility region, Mitch asked three students to hold a plank of wood up above their heads. With each student representing one of the three points of intersection, Mitch challenged them to make the highest point on the board not at one of the corners. This hands-on experiment demonstrated to the students that the highest point always occurs at one of the points of intersection. Mitch was influenced by his use of technology in his pedagogy course to assist his students to move beyond rote understanding and was able to do so even without access to that same technology.
Ann’s Probability Simulation . Ann, a preservice teacher in our mathematics methods course, wanted to design a lesson for students to use experimental probabilities to closely approximate theoretical ones and to discuss the law of large numbers. She created an interactive spreadsheet that would quickly generate a large amount of random data. The experiment in Ann’s lesson was to draw a random card from a standard deck 2,000 times. The user is able to specify a card (e.g., king of spades), and the spreadsheet tallies the number of times that card was picked out of the 2,000 trials. In addition, the tallies shown in Figure 4 allowed the students to see the similarity in results for picking each of the 52 cards, as well as the 4 suits and the 13 different face values. She used this spreadsheet in a peer teaching episode to help other mathematics education students calculate experimental probabilities and to lead them to thinking about the theoretical probability of picking a single card (1/52), a specific suit (1/4), and a specific face value (1/13).
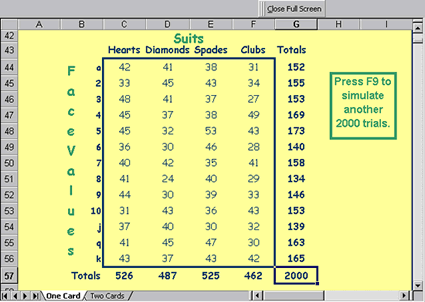
Figure 4. Frequency chart for all cards chosen from 2,000 random draws
Matt’s Geometry Web Resource . After completing his student teaching, Matt created the Geometry Gala, an interactive web-based geometry resource for students and teachers. Geometry Gala contains statements of many of the more commonly studied theorems concerning angles, circles, triangles and quadrilaterals, a collection of downloadable Geometer’s Sketchpad interactive sketches to illustrate each of these theorems, and movies of these sketches with sound descriptions. (Figure 5.) Matt’s Geometry Gala can be accessed at
http://curry.edschool.virginia.edu/teacherlink/math/geometrygala/ggg_contents.html .
Figure 5. A screen shot from the Geometry Gala
Mike’s Calculator-Based Ranger Lesson . Mike made regular use of graphing calculators and CBLs during his student teaching. On one occasion he asked students to work in small groups to ‘create’ graphs by ‘walking them’ in front of a TI-Ranger. He began by asking students to walk the ‘usual’ graphs (e.g., increasing with constant slope, horizontal) and asked them to discuss their methods and observations and to interpret and analyze their findings with respect to slope and distance-rate-time relationships. In order to assess whether or not his students really understood these relationships, he asked them to create more difficult and even impossible graphs. For example, he asked them to create parallel lines, spikes, and loops. In each case he allowed students to experiment with walking the graphs. He asked them to explain why they walked what they walked, why they thought the graphs were difficult or impossible, and, most importantly, how their methods and findings related to the concept of slope and distance-rate-time relationships.
Kris’s Geometry Lesson . One day while student teaching, Kris was teaching a lesson on the angles formed when two parallel lines are cut by a transversal. During the first half of class, the students were in the computer lab using The Geometer’s Sketchpad . Students worked individually at the computer and referred to a written exploration guide Kris had created. Not only did the guide provide the students with instructions of the mathematical exploration but also of the technology features of Sketchpad necessary to complete the exploration. As the students were following the written guide, Kris facilitated the students to make conjectures about pairs of congruent angles in their sketches. Students recorded their conjectures as they followed through a series of explorations, as seen in Figure 6. After approximately 45 minutes in the computer lab, the students went back to their classroom with their completed exploration guide in hand. The class summarized the conjectures they had made in the computer lab before Kris gave each student a printed sheet with the Corresponding Angle Postulate , the Alternate Interior and Exterior Angles Theorems , and the Consecutive Interior Angles Theorem formally stated. She purposefully left space under each of the theorems for the students to provide a formal proof. She carefully explained how their explorations in the computer lab did not provide mathematical proof of the theorems; their explorations were used to conjecture the theorems. Kris used the remaining class time to have students formally proof the conjectures they had made in the lab. Although Kris had seen many activities in her methods class where The Geometer’s Sketchpad was used, the particular activity she used in her class was not one of them. She transferred what she had learned in her methods class to create a short exploration that was useful for the objectives of her particular lesson.

Figure 6. Kris’ Exploration Guide
Jerry’s Model of Projectile Motion . For a class project in our course, Jerry, then a preservice teacher, wanted to use the interactive capabilities of a spreadsheet to help students explore projectile motion and make connections with parametric equations, trigonometry, and quadratic functions. Jerry created the projectile motion environment (Figure 7) to allow students to manipulate various parameters in a parametric equation (initial altitude, initial velocity, and launch angle). With the time scroll bar, students can animate the motion of the object and explore how long it takes for the object to reach its maximum altitude and when the object will hit the ground. By varying the other parameters, the students can explore how each will affect the path of the object and which values will maximize or minimize altitude and horizontal distance. Jerry believed that manipulating different parameters and visualizing the path of the object could make the mathematical equations used to describe projectile motion relevant and meaningful to students. During his peer lesson, he engaged the class in a rich discussion comparing the parameters in the parametric equation to the parameters in trigonometric and quadratic functions.
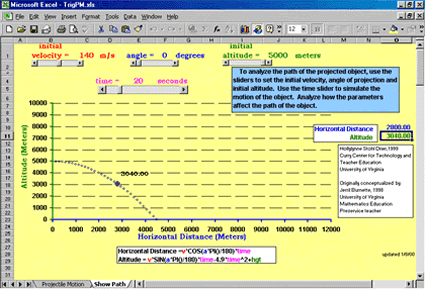
Figure 7. Interactive spreadsheet to explore projectile motion
Final Thoughts
We realize that these PSTs are just beginning to develop into teachers who can incorporate technology into their teaching. We are encouraged by their initial efforts to help students learn mathematics conceptually and apply mathematics meaningfully. Other researchers (Olive & Leatham, 2000) have documented that using technology as a tool for learning mathematics is not enough to ensure PSTs will use technology as a teaching and learning tool in their own classrooms. Many factors affect the development of PSTs’ use of appropriate technology tools. Many PSTs need sustained interactions with technology throughout their teacher education programs, especially in the context of pedagogy courses, combined with meaningful field experiences and support to learn to value the affordances of a technology-enabled classroom and embrace teaching and learning opportunities with technology. In addition, PSTs’ beliefs about teaching and learning are central to their development. However, PSTs’ past learning experiences with technology, as well as their engagement and interactions in technology-enabled learning activities like the ones we advocate, have strong influences on their belief systems. For a discussion of how PSTs’ beliefs about teaching and learning mathematics are affected by experiences with technology, see Drier, 2001. We hope that our guidelines, learning activities, and examples motivate mathematics teachers and educators to reflect on and discuss the use of technology in their teaching.
References
Browning, C., & Klespis, M. (2001). A reaction to Garofalo, Drier, Harper, Timmerman, & Shockey. Contemporary Issues in Technology and Teacher Education , [Online serial], 1 (2). Available:
https://citejournal.org/vol1/iss2/currentissues/mathematics/ .
Drier, H. (2001, March). Beliefs, experiences, and reflections that affect the development of techno-mathematical knowledge . Proceedings of the Twelfth International Meeting of the Society for Information Technology and Teacher Education, Orlando, FL.
Garofalo, J., Drier, H.S., Harper, S., Timmerman, M.A., & Shockey T. (2000). Promoting appropriate uses of technology in mathematics teacher preparation . Contemporary Issues in Technology and Teacher Education , [Online serial], 1 (1). Available:
https://citejournal.org/vol1/iss1/currentissues/mathematics/ .
Hiebert, J., & Lefevre, P. (1986). Conceptual and procedural knowledge in mathematics: An introductory analysis. In J. Hiebert (Ed.), Conceptual and procedural knowledge: The case of mathematics (pp. 1-27). Hillsdale, NJ: Lawrence Erlbaum.
Olive, J., & Leatham, K. (2000). Using technology as a learning tool is not enough . Paper presented at the International Conference of Technology in Mathematics Education, Auckland, New Zealand.
Skemp, R. (1978). The psychology of learning mathematics . Hillsdale, NJ: Lawrence Erlbaum.
Contact Information
Suzanne Harper
Center for Technology and Teacher Education
University of Virginia
1912 Thomson Road
PO Box 400279
Charlottesville, VA 22904-4279
[email protected]
![]()