Much of the reform in mathematics education advocates teachers supporting appropriate use of technology and teacher knowledge structures that incorporate knowledge about subject matter, learners, pedagogy, curriculum, and schools (Ball & Stacey, 2005; National Council of Teachers of Mathematics [NCTM], 2000; Niess, 2005). Integration of such techniques in effective manners allows teachers and students to access advanced concepts, incite mathematical discourse, and represent abstract concepts. Mishra and Koehler’s (2006) technological pedagogical content knowledge (TPCK) framework lies at the core of understanding how technology can help remedy some of the problems of teaching and learning. TPCK brings together knowledge about content, pedagogy, and technology as interconnecting factors affecting the development of effective teaching with technology (Mishra & Koehler, 2006).
Mathematical TPCK, dissimilar from knowledge of all three concepts individually, refers to the intersection of knowledge of mathematics with knowledge of technology and with knowledge of teaching and learning. It underlines the notion of using technology as a tool to construct teacher and student mathematical knowledge (Mishra & Koehler, 2006). In order for technology to become a tool for learning mathematics, mathematics teachers must develop “an overarching conception of their subject matter with respect to technology and what it means to teach with technology – technology pedagogical content knowledge (TPCK)” (Niess, 2005). Shulman (1987) defined content knowledge as the knowledge about the subject (i.e., knowledge of mathematics and mathematical representations), while knowledge of students, knowledge of teaching, and knowledge of educational contexts characterize pedagogical content knowledge. The sum and intersection of technological knowledge, pedagogical knowledge, and content knowledge serve as a framework for effective mathematics teaching and learning.
To be prepared to teach mathematics adequately, teachers must have a comprehensive understanding of TPCK. As mathematics teachers think about teaching with technology, they should concurrently consider how to teach mathematical concepts in such a way that students can experiment with ideas, make conjectures, test hypotheses, and form generalizations.
Likewise, in order for technology to support effective mathematics teaching, teachers must develop or use appropriate mathematics tasks that capitalize on the strengths of technology. Because of the wealth of available technology resources, a challenge for teachers is in learning how to selective appropriate and effective technology tools for mathematics teaching and learning. As views of technology as a demonstration tool expand to views of technology as more of a knowledge construction tool, teachers will experience how to select, evaluate, design, teach, and learn using this powerful resource.
As the NCTM (2000) highlighted, technology integration in the teaching and learning of mathematics is a necessity. As the necessity and availability of technology in mathematics classrooms increases, so must supporting teachers in their practices, professional development, and development of TPCK (Newby, Stepich, Lehman, & Russell, 2000; Roblyer & Edwards, 2000). Although preparing teachers to use technology appropriately is a complex task (Mergendoller, 1994), research suggests that such professional development must entail both conceptual and pedagogical issues. An important challenge is to identify how to prepare mathematics teachers to teach in the 21st century using TPCK and what they need to know to be able to do so.
Procedures
This article describes experiences gained from a professional development project designed to prepare in-service eighth-grade mathematics teachers to develop, explore, and advance TPCK in the teaching and learning of algebra. It details and describes the process of the participating teachers’ mathematical activities and teaching and learning tasks, each of which required a TPCK framework. The project helped teachers become more effective in facilitating students’ learning through strengthening teachers’ technological and pedagogical content knowledge of algebra.
Participants and School District
This initiative provided professional development to 20 middle school teachers from six different schools in the same area. Although the schools were in the same district, three of the schools were in a rural setting and three in an urban setting. Participating teachers, all women from various backgrounds, applied to participate in the project, were paid a small stipend for attending sessions, and were given various mathematics materials and supplies (e.g., TI Nspire technology, algebra tiles classroom sets, and algebra blocks) to supplement their teaching.
Only two of the teachers had more than 2 years of Algebra I teaching experience. Slightly over two fifths of the teachers had been teaching for at least 10 years, three of the teachers had 3 or fewer years of teaching experience, and the remaining teachers had teaching experience ranging from 3 to 10 years.
With the exception of one multigrade charter school teacher, all participants were public school teachers teaching at least one eighth-grade Algebra I course, with an average of 21 students in each class. All 20 participating teachers had middle school general teaching certifications; none had secondary mathematics certification.
The district, rated “Academically Acceptable” by the state education agency for the past 2 years, had a 60% pass rate on the state standardized eighth-grade mathematics assessment exam. Over 80% of the district’s student population was classified as minorities, with 16% of the students classified as English language learners. Eighty-two percent of the district’s students were eligible for free or reduced price lunch programs.
In response to a district mandate for all eighth-grade students to be enrolled in Algebra I, all participating teachers began teaching eighth-grade Algebra I for the first time during the academic year following the beginning of the professional development sessions. Each teacher received 120 professional development hours, including 60 hours of summer professional development and 60 hours of academic year professional development, each consisting of fifteen 4-hour sessions. Summer sessions focused on conceptual knowledge, while the academic year agenda targeted pedagogical techniques for developing and implementing effective Algebra I classroom activities and instruction for all students, particularly those from underrepresented groups.
Project Details
The primary goals of the professional development sessions were to (a) offer participating teachers new opportunities to creatively formulate and communicate TPCK, (b) increase their understanding of algebraic concepts, and (c) develop their problem-solving skills with an emphasis on modeling concepts and using technology. The professional development program guided teachers in learning about planning for teaching and learning algebra using technology. Teachers increased their level of content knowledge, learned to develop student-centered activities, identified specific activities that guided their planning and teaching of algebra, increased their knowledge and appropriate use of technology in the teaching and learning of algebra, explored eighth-grade algebra projects, examined how algebra fits into the curriculum, experimented with instructional strategies, and engaged in constant mathematics dialog. Additional instructional activities included writing in electronic journals, designing technology-based curricular materials, using graphing calculators, and using mathematical software.
As detailed in an outline of the summer and academic year sessions in Appendix A and B, respectively, sessions encouraged cooperative work, reflection on teaching experiences, and exploration of a variety of solution strategies. The sessions were organized and conducted by the author, a mathematics educator charged with the responsibility of preparing preservice mathematics teachers and delivering continuing education to in-service mathematics teachers to advance TPCK and a colleague with numerous years of experience teaching mathematics at the postsecondary level. A discussion of three session experiences is presented later in the article.
Methods
Participant journal entries and observations of interactions and discussions between participants were categorized and analyzed using a TPCK content analysis framework (Mishra & Koehler, 2006). Identified participant discussions, interactions, and perceived benefits of participating in the project were noted in one or more of four categories developed to describe general themes in varying levels of TPCK development. The four categories included technological pedagogical knowledge (TPK), technological content knowledge (TCK), pedagogical content knowledge (PCK), and technological pedagogical content knowledge (TPCK).
Descriptors or themes reflecting participants’ development of an understanding of how technology usage serves as an avenue for multiple representations of algebraic concepts were sorted into the TCK category, and those indicative of participants’ understanding of how teaching algebra changes as a result of using a variety of available technologies were grouped in the TPK category. The PCK category highlighted indicators of how participants’ understanding of algebraic concepts influenced their teaching of algebra.
Naturally, the TPCK category grouped blends of all three categories. Responses in one category often intersected with one of the three other content analysis categorizations. All observations and journal entry details were categorized using at least one of the four descriptors to describe participants’ levels of TPCK in teaching and learning algebra.
Discussion of Sample Activities
The experiences of the author and summaries from three different professional development sessions are presented in the following section. Activities and discussions from the professional development sessions focused on using technology to represent algebraic ideas in verbal, symbolic, and graphic forms. As a part of the TPCK initiative, participants were required to consider what algebraic reasoning means to them and the various forms that students concentrate on, think together about how students can develop their algebraic reasoning and transition from calculations to mathematical analysis, and assess the role of resources used in the teaching and learning of algebra.
Activity 1: Analysis of a Transfer Problem
One of the many activities that teacher participants engaged in involved transfer problems. For students to develop an understanding of functions, they must have opportunities to solve problems that require them to transfer between algebraic, numeric, and graphic representations (Cunningham, 2005). Knuth (2000) reported that a majority of students fail to recognize or create transfer between graphic and algebraic representations. Research has confirmed that student difficulties with certain types of transfer problems are results of instructional factors. Despite graphing calculator usage and availability, students are given few opportunities to solve graphic-to-numeric transfer problems. Research has suggested that student achievement is positively affected when students use curricula designed with graphing calculators as a primary tool (Kastberg & Leatham, 2005).
To make meaning of certain problem situations, it is imperative that students model these situations graphically and use graphing to find solutions to these problems. As a part of a project session focused on exploring the effects of using multiple representations in solving linear equations and inequalities, project teachers were asked to solve an inequality given in algebraic form, such as
![]() ,
,
and then solve the same inequality given only its graphic representation. All participating teachers were able to solve the inequality in algebraic form successfully. However, only slightly less than half of the teachers were able initially to solve the same inequality in graphic form. Although teachers were able to graph both inequalities successfully by hand and with a graphing calculator, teachers were not able to recognize the solution to the inequality based solely on the graph.
After extensive discussion, a group of teachers collectively outlined steps to respond to the following task:
Solve ![]() using only the given graph of its inequality.
using only the given graph of its inequality.
An excerpt from one group’s conversation follows. Research comments are in brackets at the end of each of the teacher’s statements.
| Teacher A: | I think we should first make an attempt to represent what we are thinking. |
| Teacher B: | We already have the graphs. We need to figure out the answer. |
| Teacher A: | No…we already know the solution to the inequality. We found that using basic algebra. This is different. How can we verify it using only the graph? What strategy would you use to explain this to your students? [This is an example of the teacher’s PCK. She explores ways to make this notion comprehensible to her students.] |
| Teacher C: | Let’s start over. Graph the inequality on the Nspire. Well … I don’t know how to graph it with the inequality.… But we can graph the two sides separately but on the same page. [This is an example of the teacher’s TCK. She explores how to graph an inequality using a graphing device.] |
| Teacher A: | I’m not sure if that will help but at least we will be able to actually see the lines and move them to make one bigger than the other. [This is an example of the teacher’s TCK. She understands technological content.] |
Next, the teachers explored and manipulated the graphs of y1 = 2(x – 4) and
![]()
using the graphing device. They zoomed in on critical points and briefly explored the numerical table of the representation.
| Teacher A: | Showing students this with computer software would be great. OK, so look … no matter how I move the lines, this part of this one is always on top of this one. [This is an example of the teacher’s TPK. She understands that more than one technology tool exists to help students make connections between effects of manipulating graphs and solving inequalities.] |
| Teacher C: | Right. Yes. You are right. Well, that’s what we need to know. Right? Look – values on this line are bigger than that line anytime x is at least … [This is an example of the teacher’s TCK. She understands how to use the graphing device to explore the effect altering either graph has on changing x values.] |
| Teacher B: | …Negative 9 and a half. So how would I explain this to my students? The solution could be obtained quicker from the graph than when we solved the inequality by hand in the beginning. It makes so much sense. “Greater than” means “When is the left bigger than the right?” [This is an example of the teacher’s TPCK. She reflects on how a teacher can show students how to perform the technological procedures and relate solving inequalities in a coherent way during her teaching.] |
Analysis of teacher discussions and actions during this task revealed multiple examples of the teachers’ exploration and development of TCK, TPK, PCK, and TPCK. Although the most prominent knowledge category is highlighted, themes intersect multiple categories. In particular, teachers almost always showed some evidence of TCK. As noted in the transcript excerpt, the teachers agreed to utilize a representation that amplified their conceptual understanding and served as a catalyst for their critical thinking. They argued that through representing the graph on a graphing calculator, they would be able to expose diverse aspects of graphing inequalities, process information in a more meaningful and varied way through building tables, tracing curves, and zooming in on critical points, and minimize mastered plotting tasks. As a result of the graphing calculator usage, the teachers became more involved in asking and answering “what if” and “how to teach” questions that challenged their pedagogical and content knowledge because of their technology usage.
As a means of fostering the development of TPCK, all participants were required to reflect in a journal entry how they and their students could overcome the hurdles of moving from calculations to mathematical analysis, particularly through the integration of technology in this teaching and learning shift. In her entry, one teacher wrote,
I was initially embarrassed that I couldn’t find the solution by looking at the graph without other’s help. I can’t believe how much this simple activity has changed my thinking about the types of questions I ask of my students and of my own teaching. We are so used to “finding the answer” that we forget what the answer actually means. If I would have started this task with translating what that answer I got from working the problem by hand (with no graph) meant, I could have easily been able to find the answer from the graph.
This entry embodies multiple references to the teacher’s development of varying levels of TPCK. She focused on her pedagogical knowledge but intersected that exploration with content and technological knowledge.
The purpose of this task was not only to require the teachers to learn new technological practices, but also have them adjust their current information technology use and integrate these new practices into their existing pedagogical and content knowledge practices. This process situated the teachers’ analysis of their own algebraic representation and manipulation in their own learning and instruction. In reflecting on this challenge, teachers wove together technology, content, and pedagogy to focus on their instructional goals and the math content of solving inequalities using only their corresponding graphs. In doing so, the teachers discovered that the delay in their ability to successfully address such transfer problems was not due to deficiencies in their mathematics foundation but instead due to inadequacies in their interpretation skills. Teachers who do not have these understandings can misrepresent content to their students (Ball & McDiarmid, 1990).
Activity 2: Analysis of Virtual Manipulatives
Teachers participating in this professional development project were provided access to virtual manipulatives that directly support the initiative’s vision of an integrated mathematics and technology curriculum. Most of the participating teachers had some experience with classroom use of physical manipulatives, but none had familiarity with using virtual manipulatives, an electronic version of concrete manipulatives. Virtual manipulatives are dynamic electronic representations that combine characteristics of physical and pictorial models (Moyer, Bolyard, & Spikell, 2002). They are generally free, can be accessed through various online mediums, and are often paired with associated lessons or activities for use in the mathematics classroom.
A recent review of research indicates that students using virtual manipulatives either alone or in combination with physical manipulatives demonstrate gains in mathematics achievement and understanding (Bolyard, 2006; Moyer, Niezgoda, & Stanley, 2005; Reimer & Moyer, 2005; Suh & Moyer, 2007) and appear to be more engaged and on task than when using physical manipulatives (Drickey, 2000). Virtual manipulatives enable students and teachers to represent abstract, mathematical concepts in concrete ways and to link these concepts to prior knowledge. Students’ abilities to represent abstract concepts and translate among representations, including internal and external representations, facilitate deeper understanding of mathematical concepts (Goldin, 2003).
As a part of two professional development sessions focused on exploring how virtual manipulatives can be used in the teaching and learning of algebra, participating teachers first explored an electronic library of interactive, Web-based virtual manipulatives at the National Library of Virtual Manipulatives (http://nlvm.usu.edu/). Reimer and Moyer (2005) said that in order for teachers to use virtual manipulatives effectively in the classroom, they must understand how to use representations for mathematics instruction and how to structure a mathematics lesson in which students use technology, and they must be comfortable with technology. In pairs, teachers examined content from district lesson modules and then compared each module’s technology alignment and content with the NCTM standards (2000) and state Algebra 1 standards.
Teachers modified five lessons over the course of the sessions by integrating the use of virtual manipulatives in each. In doing so, participating teachers had to determine the type of virtual manipulatives appropriate for each lesson and how each would be used. Graphing devices were the most frequently used of all virtual manipulatives. The teachers’ uses of virtual manipulatives in the modified lessons focused primarily on investigating and understanding mathematical concepts (i.e., developing TCK) and introducing new mathematical concepts (i.e., developing TPCK). The teachers’ level of TPCK was categorized and analyzed in these sessions based on their interactions and journal entries. The following description of teachers’ exploration of the classic counterfeit coin problem provides an example.
Participating teachers were challenged to use an electronic manipulative to investigate and explain the counterfeit coin problem and identify what algebra was needed to solve the problem. The counterfeit coin problem is a fascinating learning activity that reads,
In a collection of n coins, all coins have the same weight except for one coin, known as the counterfeit coin, which is heavier than the others. Plan a weighing scheme to identify the counterfeit coin in as few weighings as possible.
The teachers used a counterfeit coin virtual manipulative (http://nlvm.usu.edu/en/nav/category_g_3_t_2.html), which included a two-pan balance scale and selection of the user’s choice of number of coins, to reason through the problem. The scale could not measure the weights of the collections but could only determine which of two collections was heavier.
The teachers initially attempted to complete the activity using the virtual scale simply to meet the requirements of the task, but they soon discovered even greater value in the activity and were challenged to explain how the manipulative worked through extracting the mathematics from the activity. In thinking through and carrying out a strategy, teachers were forced to analyze various possibilities and draw logical inferences. (See Figure 1 for an example of one of the scale trials.) They discovered the key to the activity was in realizing how the coins could be grouped into sets (i.e., left pan on scale is heavier, pans balance on scale, or right pan on scale is heavier) and deducing relationships between those sets. Efforts of the teachers reflected their desire to show how the problem could be represented and solved symbolically rather than by experimentation. An excerpt of a pair of teachers’ conversation about the problem follows:
| Teacher A: | Let’s begin by restating the problem in our own words.… Or should we try to figure out what’s the point of the whole problem before we start? Where’s the math … I mean algebra? [This is an example of the teacher’s PCK. She explores how to link the problem statement to the teaching or learning of algebra.] |
| Teacher B: | No. Let’s start and then reflect. So from a group of coins that all look alike, find which coin weighs the most. Right? |
| Teacher A: | OK, but we need a plan on how to do that. Let’s just play around with the manipulative first and see if we notice anything. Try separate first and then we’ll compare. [This is an example of the teacher’s TCK. She attempts to understand the technological content through exploration.] |
Participants worked at separate computer stations for about 25 minutes. Each experimented with the virtual manipulative and wrote down questions and discoveries.
| Teacher A: | I started with a small number of coins. I did 8. I put 4 coins on each side. I knew the counterfeit coin would be on the heavier side. I started removing pairs of coins, looking for cases where the scale would not be equal. This is a lot like balancing an algebraic equation. It justifies how changing one side of the scale changes the whole thing. [This is an example of the teacher’s TPCK. She considers how to organize an instructional strategy so that the manipulative provides possible opportunities for students to discover the meaning of balancing an equation.] |
| Teacher B: | Did you come to any conclusions? |
| Teacher A: | I used the same strategy several times and always found the counterfeit coin. I checked to see if the scale was balanced or not. I wish I knew how to find it quicker. It always took me several tries and it gets harder with more coins. [Although the teacher does not clarify her statement here, in a later discussion, she explained that the tool would sponsor serious classroom mathematical discourse (i.e. discussions about what happens if the two sets balance). This suggests the teacher’s TPCK.] |
| Teacher B: | But that’s the nice thing about this manipulative. You can continue to change values and immediately see the outcome. Every time I tried a new strategy, I was able to check it and then change my thinking to match what happened.… I always ruled out wrong solutions in order to find the counterfeit coin. [This is an example of the teacher’s TPCK. She explains how the tool helped her understand the content. She also implies the idealness of the manipulative as a teaching tool with an option of modifying degrees of complexity of the problem.] |
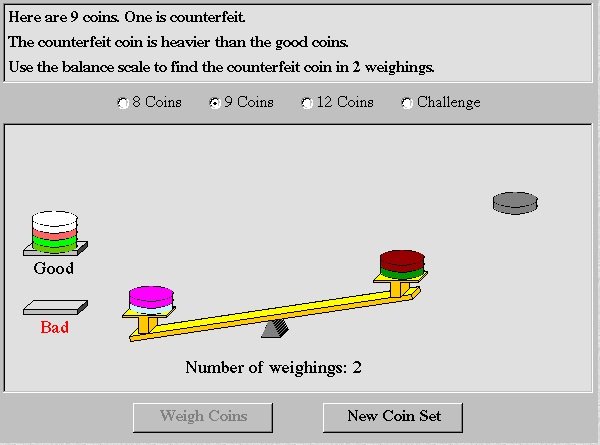
Figure 1. Counterfeit coin trial (http://nlvm.usu.edu/en/nav/category_g_3_t_2.html).
Analysis of teacher discussions and actions during this task revealed multiple examples of the teachers’ exploration and development of TCK, TPK, PCK, and TPCK. Although not categorized in the data, many teachers also developed pedagogical knowledge as a result of work on the counterfeit coin problem. They constantly considered how the tool would effect or enhance instructional strategies. One teacher from a different group wrote “I also think this coin problem would help students develop their problem solving skills, particularly developing skills like developing an initial strategy, testing the strategy, and adapting the strategy if it does not work.”
Activity 3: Analysis of GeoGebra
Participating teachers were introduced to the free Web-based software program GeoGebra (http://www.geogebra.com) during the final professional development sessions. GeoGebra, a dynamic mathematics software program that links secondary and postsecondary school geometry, algebra, and calculus, was created to help students gain a better understanding of mathematics. The software can be used both as a teaching tool to explore and discover mathematical properties and as a tool for the creation of interactive teaching materials. GeoGebra provides two representations of each mathematical object in its algebra and graphics windows, where changing an object in one of the windows results in its immediate representation in the other window.
Because GeoGebra provides multiple representations of mathematical objects, it helps users discover connections between equations and their graphical representation. Teachers were able to influence both the algebraic and the graphical representation of an object (see Figure 2). They explored transitions from graphical to algebraic representations and algebraic to graphical representations. They also used Geogebra to create electronic, interactive applets focusing on various algebraic concepts and constructions, including plotting functions, creating animated worksheets, and graphing specific equations.
One veteran teacher wrote of her delight with using the program as a teaching tool. In a journal entry she said, “I really enjoyed the software’s ability to create active and problem-oriented teaching.… Also, students would be able to make immediate discoveries that explain the algebra behind the process.” This statement reveals her shift to developing TPCK. During earlier project sessions, her emphasis was primarily on technological knowledge. Initially, she rarely made a connection between the technology, pedagogy, and content. As part of a separate assignment, another teacher chose to investigate linear equations and their corresponding graphs in a GeoGebra applet. Her entry reflected primarily TCK. In short, she stated, “I spent most of the time investigating how changing the slope of the line in one window affected the other window.”
Conclusions
This paper presented components of a professional development project that offered new experiences in creative work for in-service Algebra I teachers. A primary goal of this professional development project was to develop and advance teachers’ TPCK. Analysis of the data under the TPCK framework was useful in diagnosing in-service mathematics teachers’ need to intersect, rather than isolate, these three knowledge bases. Participating teachers were not labeled as a content expert, technology expert, or pedagogical expert but instead classified as developing professionalism simultaneously in all three components.
Analysis of the professional development sessions revealed the need for more professional development focused on enhancing teachers’ ability to connect mathematical ideas using technology and on their pedagogical and content skills to work with multiple representations of mathematical ideas. This trend was noted in instances of data analysis, where teachers focused more on developing TCK in comparison to TPCK or PCK. Another important finding from the data analysis is that teachers need opportunities to explore how to integrate nontraditional forms of technology effectively into both routine and nonroutine algebraic classroom instruction. More specifically, teachers need help in making the transition from using technology-based manipulatives for illustrating mathematical concepts (TCK) to utilizing these tools as means for exploration and discovery leading to students’ deep conceptual understanding of mathematics (TPCK).
In an informal exit discussion, all 20 participating teachers answered yes to the question “Did the professional development sessions provide you with valuable insights of how to use technology to explore, investigate, and verify new mathematical situations?” Responses to this question showed clear evidence of the teachers’ TPCK advancement. Challenges encountered in the professional development sessions included getting teachers to focus on technology, issues, and pedagogy collectively in lieu of focusing simply on technology and the teachers’ disposition toward new technology. In addition, no emphasis was placed on considering possible limitations of integrating technology in the teaching and learning of algebra. The sessions primarily focused on identifying the benefits of developing, exploring, and advancing the teachers’ TPCK.
References
Ball, D. L., &. McDiarmid, G.W. (1990). The subject matter preparation of teachers. In R. Houston (Ed.), Handbook of research on teacher education (pp. 437-449). New York: Macmillan.
Ball, L., & Stacey, K. (2005). Teaching strategies for developing judicious technology use. In W. J. Masalski & P. C. Elliott (Eds.), Technology-supported mathematics learning environments: Sixty-seventh yearbook (pp. 3-15). Reston, VA: National Council of Teachers of Mathematics.
Bolyard, J. J. (2006). A comparison of the impact of two virtual manipulatives on student achievement and conceptual understanding of integer addition and subtraction. Dissertation Abstracts International, 66(11), 3960A.
Cunningham, R. (2005). Algebra teachers’ utilization of problems requiring transfer between algebraic, numeric, and graphic representations. School Science and Mathematics, 105(2), 73-82.
Drickey, N. A. (2000). A comparison of virtual and physical manipulatives in teaching visualization and spatial reasoning to middle school mathematics students. Dissertation Abstracts International, 62(02), 499A.
Goldin, G. A. (2003). Representation in school mathematics: A unifying research perspective. In J. Kilpatrick, W. G. Martin, & D. Schifter (Eds.), A research companion to principles and standards for school mathematics (pp. 275-285). Reston, VA: National Council of Teachers of Mathematics.
Kastberg, S., & Leatham, K. (2005). Research on graphing calculators at the secondary level: Implication for mathematics teacher education. Contemporary Issues in Technology and Teacher Education, 5(1), 25-37.
Knuth, E. (2005). Student understanding of the Cartesian coordinate connection: An exploratory study. Journal for Research in Mathematics Education, 31(4), 500-508.
Mergendoller, J. R. (1994). The Curry School of Education, University of Virginia. In Exemplary approaches to training teachers to use technology, vol. 1: Case studies (pp. 4.1-4.24). Novato, CA: Beryl Buck Institute for Education.
Mishra, P., & Koehler, M.J. (2006). Technological pedagogical content knowledge: A new framework for teacher knowledge. Teachers College Record, 108(6), 1017-1054.
Moyer, P.S., Bolyard, J., & Spikell, M.A. (2002). What are virtual manipulatives? Teaching Children Mathematics, 8(6), 372-377.
Moyer, P. S., Niezgoda, D., & Stanley, J. (2005). Young children’s use of virtual manipulatives and other forms of mathematical representations. In W. J. Masalski & P.C. Elliott (Eds.), Technology-supported mathematics learning environments: Sixty-seventh yearbook (pp. 17-34). Reston, VA: National Council of Teachers of Mathematics.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
Newby, T. J., Stepich, D. A., Lehman, J.D., & Russell, J. D. (2000). Instructional technology for teaching and learning: Designing instruction, integrating computers and using media. Columbus, OH: Prentice Hall.
Niess, M. L. (2005). Preparing teachers to teach science and mathematics with technology: Developing a technology pedagogical content knowledge. Teaching and Teacher Education, 21, 509-523.
Reimer, K., & Moyer, P.S. (2005). Third graders learn about fractions using virtual manipulatives: A classroom study. Journal of Computers in Mathematics and Science Teaching, 24(1), 5-25.
Roblyer, M.D., & Edwards, J. (2000). Integrating educational technology into teaching. Columbus, OH: Prentice Hall.
Shulman, L. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4-14.
Shulman, L. (1987). Knowledge and teaching: Foundations of the new reform. Harvard Educational Review, 57, 1-22.
Suh, J. M., & Moyer, P. S. (2007). Developing students’ representational fluency using virtual and physical algebra balances. Journal of Computers in Mathematics and Science Teaching, 26(2), 155-173.
Author Note:
Sandra Richardson
Lamar University
[email protected]
Outline of Summer Professional Development Sessions
All sessions began with a Teachers Helping Teachers component, where each participant shared (in small groups) progresses and challenges from the week and reflected on how the last session changed either an action or thought in their teaching or learning. All activities and tasks required more than one solution strategy. Most activities also required paired-work.
Session | Topic |
1 | Identifying Patterns |
2 | Independent and Dependent Functions Changing Perimeter |
3 | Parent Function Formalizing Slope and y-intercept |
4 | Slope-Intercept Formula Graphing Software Demo/Exhibit |
5 | Stack of Cups Introduction/Distribution of Graphing Calculators |
6 | Applications of Slope and Intercept Changes in M and B Graphical, Tabular and Symbolic |
7 | Reflections Solving Equations Using Concrete Models Graphing Calculator Skills |
8 | Building with Blocks Systems of Equations |
9 | Scavenger Hunt Classroom Connections Revisited |
10 | Classroom Connections Pythagorean Theorem |
11 | Graphing Skills with Technology |
12 | Quadratics and Solutions |
13 | Exponential Relationships |
14 | Inverse Variations |
15 | Curves Ahead Classroom Connections Revisited |
Appendix B
Outline of Academic Professional Development Sessions
All sessions began with a Teachers Helping Teachers component, where each participant shared (in small groups) progresses and challenges from the week and reflected on how the last session changed either an action or thought in their teaching or learning. All activities and tasks required more than one solution strategy. Most activities also required paired-work.
Session | Topic |
1 | What is Algebra? |
2 | Investigation of Slope, Linear Equations, and Inequalities |
3 | Hands-on Equations |
4 | Hands-on Equations |
5 | Algebra Tiles & Algebra Blocks |
6 | Algebra Tiles & Algebra Blocks |
7 | Graphing Calculator Skills TI-Nspire Technology |
8 | Virtual Manipulatives |
9 | Virtual Manipulatives |
10 | Pythagorean Theorem |
11 | Graphing Calculator Skills TI-Nspire Technology |
12 | TI-Nspire Technology |
13 | GeoGebra |
14 | GeoGebra |
15 | Exit Interview |
![]()