With rapid and recent advances in electronic technology, it is not surprising and, perhaps, is even expected that veteran teachers of mathematics received little to no instruction on how to use such technologies for teaching and learning mathematics. Some forms of technology have only recently been developed, while others that have been in existence for some time may not have been a part of a teacher’s precollege or teacher preparation experience. As technology evolves, so do the materials used for preparing teachers in the current era.
This article presents an overview of how electronic technology is presented in textbooks written for mathematics content courses for prospective elementary teachers (i.e., those teaching students in kindergarten through Grade 8). The commonalities present across a sample of popular textbooks, as well as the features unique to individual textbooks, are discussed. Specific attention is given to the examples in which a textbook may influence the development of technological pedagogical content knowledge (TPCK; Mishra & Koehler, 2006; Niess, 2005) in prospective teachers. For the purposes of this paper, electronic technologies are defined to be calculators (either four-function, scientific, or graphing), tablets, and computers, which include the use of Web and social media resources, along with computer software such as spreadsheets and dynamic geometry software.
Background
Professional organizations such as the International Society for Technology in Education (ISTE, 2007, 2008), the National Council of Teachers of Mathematics (NCTM, 2000, 2011), and the Conference Board of the Mathematical Sciences (2012) have advocated for the use of electronic technologies in the teaching and learning of mathematics. An ever-growing number of technological resources are available to both students and teachers. Some of these resources are content-generic (e.g., computers, tablets, SMARTBoards), while others are mathematics-specific, and can be designed for use in specific content strands of mathematics.
In statistics, for example, handheld calculators may be utilized or preprogrammed to compute measures of center, spreadsheets have capabilities to quickly produce graphical displays, and some specially designed software programs allow the user to design and run simulations. Other tools (and functions of these same tools) allow for learning and teaching within other content strands, such as arithmetic, geometry, and algebra.
Prospective teachers need experiences with these various types of technologies in order be prepared to teach mathematics in the digital age (Association of Mathematics Teacher Educators, 2006; ISTE, 2008; NCTM, 2011). In the United States, such experiences may occur within a mathematics content course. While a multitude of factors influence what actually occurs in the classroom, the textbook is a common feature in such courses.
In this article, we use this common feature – the textbook – as a lens to see how prospective teachers may use technology in learning and preparing to teach mathematics. To that end, we will address the following research questions:
- How is technology presented within textbooks for mathematics content courses for prospective elementary teachers in the United States?
- In what ways may such textbooks influence the development of technological pedagogical content knowledge?
Role of Technology
In the mathematics classroom, different types of technology may be used for various purposes. Dick and Hollebrands (2011) provided a helpful distinction between two different roles that technology may play: conveyance and mathematical action. “Conveyance technologies are those used to convey, that is, to transmit and/or receive information” (p. xi, emphasis in original), and include technology used for presentation, communication, sharing/collaboration, and assessment/monitoring/distribution. Furthermore, conveyance technologies may be used for both mathematical tasks and nonmathematical tasks; one may use presentation software or the Internet in the same way for mathematics, science, literature, or history. “Conveyance technologies are not mathematics specific,” the authors said (p. xii). Examples of conveyance technologies include presentation software, the Internet, and clickers.
By way of contrast, “Mathematical action technologies are those that can perform mathematical tasks and/or respond to the user’s actions in mathematically defined ways” (Dick & Hollebrands, 2011, p. xii). Mathematical action technologies include computational and representational tools such as calculators and spreadsheets, dynamic geometry environments, microworlds such as those found in virtual manipulatives for mathematics, and computer simulations. Additionally, while the Internet, writ large, is a conveyance technology, it does provide access to many different mathematical action technologies.
In this study, we identified the technology referenced in textbooks. When possible, we classified each reference as one pointing to a conveyance technology or a mathematical action technology. The following section connects our present study with the existing literature of mathematics textbook research.
Previous Textbook Analyses
Little research has been published on textbooks used in mathematics content courses for prospective elementary teachers in the U.S. Three notable examples are found in McCrory (2006), the National Council on Teacher Quality (NCTQ, 2008), and McCrory and Stylianides (2014). In each of these studies, the authors examined between 16 and 20 textbooks intended for use in mathematics content courses for elementary teachers – nearly the entire population of such textbooks. While these studies did not specifically address technology, they did provide grounding for the selection and examination of textbooks.
McCrory (2006) presented an analysis of 20 textbooks for prospective elementary teachers. She stated, “Most of the books are encyclopedic, including every topic that might be covered in K-8 classrooms, and treating each topic as a separate entity” (p. 21), while others were more focused on a few big ideas and presented with a narrative approach. She found that the four textbooks in her sample written by research mathematicians were more narrative in style. These four textbooks also had a higher quality of mathematical coherence and rigor than the subset of 16 textbooks not written by research mathematicians.
In a study of U.S. teacher preparation programs, the NCTQ (2008) examined the syllabi of 118 mathematics courses at 77 institutions. A total of 19 different textbooks were identified across these syllabi, and an expert panel was asked to rate the books according the adequacy of coverage of the content areas of numbers and operations, algebra, geometry and measurement, and data analysis and probability. According to the panel’s ratings, about two thirds of the courses they examined used textbooks that did not adequately cover all four of these areas. The criteria for rating was based on the presentation of 36 mathematical topics; the report gives no indication as to how references to technology may influence the quality of the presentation.
In a study of reasoning-and-proving in textbooks, McCrory and Stylianides (2014) analyzed 16 mathematics textbooks for prospective elementary teachers. Because reasoning-and-proving may be related to various topics in mathematics, they first examined the table of contents and index for references to reasoning-and-proving, such as generalizing or conjecturing. Next, they examined the pages containing the references to characterize the nature of reasoning-and-proving. Their methodology provided insight about how an instructor or student may use the textbook to gain insight on this particular mathematical activity.
As with reasoning-and-proving, technology may be applied to various topics in mathematics. However, we chose to examine each page of every chapter for technology references, instead of limiting our search to those pages referenced in the table of contents or index. Additionally, we viewed these textbooks as instruments that may impact a prospective teacher’s knowledge. In the next section, we summarize the research literature regarding various types of knowledge.
Types of Knowledge
Pedagogical content knowledge (PCK) is the unique blending of content expertise and skill in pedagogy to create a knowledge base that allows teachers to make robust instructional decisions. Shulman (1986) defined PCK as “a second kind of content knowledge…which goes beyond knowledge of subject matter per se to the dimension of subject matter knowledge for teaching” (p. 9). Since the time of Shulman’s initial work, electronic technologies have been developed at an ever-increasing rate, and it is difficult to overestimate the impact of technology on teaching and learning, particularly in the area of mathematics.
To investigate teachers’ knowledge for teaching with technology, Niess (2005) expanded on the concept of PCK and described the construct of technological pedagogical content knowledge (TPCK; later referred to in the literature as technology, pedagogy, and content knowledge, or TPACK) as “the integration of development of knowledge of subject matter with the development of technology and of knowledge of teaching and learning” (p. 510). This characterization has been so useful that, in their editorial, Bull and Bell (2009) specifically suggested using TPACK as a framework for the research of technology in mathematics teacher education.
Mishra and Koehler (2006) distinguished TPCK from the related areas technological pedagogical knowledge (TPK) and technological content knowledge (TCK). Briefly, TPK is the knowledge of using technology for teaching, using tools that may be content-neutral, such as using social media or online surveys for real-time feedback and formative assessment. On the other hand, TCK is the knowledge of how technology may be used to teach particular content, such as using dynamic statistics software to conduct a large number of trials of a simulation and, thus, provide students with an understanding of the central limit theorem. According to McBroom (2012), “Students who use technology in learning are likely to possess TCK, but they are not likely to possess TPACK. Teachers, who teach with technology, should have TCK, but they also should have TPACK in order to teach effectively” (p. 18).
In this study, we sought to identify activities within textbooks that had the potential to influence the development of a prospective teacher’s TPACK. In the next section, we provide details of our research methodology.
Research Design
Sample Selection
We analyze textbooks used in mathematics content courses for prospective elementary teachers in the United States, using existing studies of mathematics textbooks for elementary teachers (McCrory, 2006; McCrory & Stylianides, 2014; NCTQ, 2008) to assist in the identification of the most commonly used titles. Six textbooks comprised the sample for this study and are listed in Appendix A along with abbreviated names used in this paper.
All six of these textbooks (or other editions) were analyzed by McCrory and Stylianides (2014) and NCTQ (2008). The first five textbooks listed were identified as the most commonly used textbooks in the NCTQ study, and were also analyzed by McCrory (2006). The sixth textbook, SSN, was also analyzed by the NCTQ, although it was relatively new at the time. It was selected for this study, in part, because of its use at the authors’ institution.
A limitation of our sample lies in the nature of textbook publication. It is common practice for publishers to print a new edition every 3 or 4 years. In fact, two of the textbooks in our sample (BLL and MBP) have now published newer editions than those in the sample. This limitation has particular implications addressed in the Recommendations section of this paper.
Only the student editions of the textbooks were examined for this study. Furthermore, only chapter pages – those pages that were a part of the marked chapters of the textbook were examined. Other portions of the text, such as the table of contents, preface, and index, were not examined. Similarly, activity manuals and ancillary resources were not examined. In particular, the activity manual for Bec is bound with the rest of the textbook, but the manual was not examined. We did not analyze any appendices, except to note the titles of any appendices that referenced technology.
Methodology
In a prior study, Jones (2014) examined the technology references within chapters of mathematics textbooks for prospective elementary teachers that addressed topics in statistics and probability. The study described in this article extended that prior study and included every chapter of each textbook. Each chapter page was examined for references to technology. References were identified when (a) the word “technology” appeared, (b) a specific type of technology was mentioned, or (c) a portion of text was marked with a technology-related icon (e.g., a calculator or computer mouse). Internet addresses (URLs) were included as technology references. On the other hand, instances of the phrases similar to, “without using a calculator,” were not coded as technology references.
Once a reference was identified, it was coded according to the type of technology (e.g., calculator, website, or computer) and the role of technology. We used the categories of conveyance technology and mathematical action technology (Dick & Hollebrands, 2011), as well as the neutral code term for those cases where it was not possible to identify whether the reference referred to technology in a conveyance or mathematical action role. To clarify, consider these three references from MBP:
- “To keep up with the ongoing race to find a bigger prime, visit the Web site www.mersenne.org.” (p. 205)
- “As a computer expert put it, ‘It’s like Mount Everest; why do people climb mountains?’” (p. 205)
- “Using a calculator method, find the following [greatest common factors of pairs of numbers].” (p. 206)
We coded reference (a) as a website in the role of conveyance, because the URL may be used to communicate more information, but not necessarily do any mathematics. The type of technology in reference (b) is clearly a computer, but in this case the computer is not specifically used for mathematics, nor is it necessarily used for conveyance. Hence, this was coded as term for its role. Finally, reference (c) was coded as a calculator in a mathematical action role. Each reference was given a single code for the role of technology.
In terms of the location within the textbook, each reference was coded in three ways: by chapter, by page number, and by a location code. Three types of location codes were used: main text, auxiliary text, or activity. References within the main text were a part of the chapter prior to exercises, but not in a specially marked section; this included worked examples and chapter summaries. Auxiliary text was contained within a sidebar or specially marked section, usually within a box labeled with a special title such as “Technology Corner” or “Mathematical Morsel.” References within sections labeled as activities, investigations, discussions, problems, or exercises were coded as activity. Each reference was coded with exactly one location code.
Each activity reference was further coded as to whether the use of technology was required, implied, optional, or referenced only within the activity, problem, or exercise. Only one of these codes was assigned to each activity reference. Appendix B contains descriptions of these codes and example references from the textbooks in the sample.
Interrater Reliability
At the beginning of the coding process, the three coauthors each independently examined the first chapter of each textbook by identifying all of the references to technology and coding them according to aforementioned categories. These codes were compared, and any discrepancies in coding were resolved through discussion. At times, the coding framework was revised due to this discussion. The role code of term was incorporated into the framework in this manner.
Following this process, each author examined three sections (one from BasM, one from Bec, and one from BLL) and identified all of the technology references. Across the 51 pages that were examined, we agreed about the presence (or absence) of technology references on 44 pages (86%). A total of 28 references were identified; 20 of the 28 references (71%) were identified by all three authors, four were identified by two authors, and four were identified by a single author. The authors then discussed all references that were not identified until complete agreement was reached.
Next, each author coded a set of 30 references (six from LDM, 13 from MBP, and 11 from SSN) according to type of technology, role of technology, and location. There was complete agreement on 28 references (93%) for the type of technology, 24 references (80%) for role of technology, and 19 references (63%) for location. While discussing the references, we realized the need for further clarification in the definitions of codes within the role of technology and location categories. The rubric was then revised to what appears earlier in this paper, and we proceeded to code textbooks independently.
We each coded all of the chapters within two textbooks. After coding was completed, 24 references were selected from Jones’s (2014) analysis of technology references in statistics chapters. The codes for role of technology and location were compared with those collected for this study. We found all 24 references (100%) agreed for role of technology, and 22 (92%) agreed for location code.
Results
Location of References to Technology
A total of 4,879 pages, located across 103 chapters in six textbooks, were examined. Overall, 696 of those pages, within 93 chapters, contained references to technology. A total of 1,055 references were coded. Table 1 displays these statistics for each textbook in the sample.
Table 1
Location of References to Technology by Book, Chapter, and Page
| Category | Book | |||||
| BasM | Bec | BLL | LDM | MBP | SSN | |
| Total number of chapters | 10 | 16 | 14 | 14 | 16 | 33 |
| Number (percentage) of chapters with technology references | 10 (100%) | 15 (94%) | 14 (100%) | 14 (100%) | 16 (100%) | 24 (73%) |
| Total number of chapter pages | 619 | 729 | 1006 | 825 | 922 | 778 |
| Number (percentage) of pages with technology references | 79 (13%) | 68 (9%) | 138 (14%) | 88 (11%) | 252 (27%) | 71 (9%) |
| Total number of technology references | 93 | 71 | 169 | 152 | 451 | 119 |
Within each textbook in the sample, more than half of the chapters contained references to technology. In four textbooks, technology references were present in every chapter; Bec contained technology references in every chapter except for the final chapter (focused on probability), and nine chapters in SSN did not reference technology. SSN has more than twice as many chapters as any of the other textbooks, so a smaller proportion of chapters may not actually mean that fewer mathematical topics incorporate technology.
In terms of the proportion of pages that contained technology references, both Bec and SSN were at the lower end, with approximately 9% of pages containing technology references. At the other extreme, more than one fourth of the pages in MBP contained technology references, more than twice that of BLL, which had the second-greatest number of references.
The chapters containing more than 10% of the references for a particular textbook are listed in Table 2. By way of contrast, there were chapters in Bec and SSN that contained no references to technology. In Bec, the chapter with no technology references was titled “Probability.” In SSN, these chapter titles were “Computing with Fractions,” “Integers and Other Number Systems,” “Polygons,” “Symmetry,” “Tessellations,” “Area, Surface Area, and Volume,” “Counting Units Fast: Measurement Formulas,” “Determining More Complicated Probabilities,” and “Special Topics in Probability.”
Table 2
Chapters Containing Relatively Many References to Technology
Book | Chapters with More Than 10% of the Technology References for a Textbook (Number of References) |
| BasM | Uncertainty: Data and Chance (19) The Four Fundamental Operations of Arithmetic (18) Extending the Number System (10) |
| Bec | Number Theory (10) Geometry of Motion and Change (10) |
| BLL | Decimals and Real Numbers (44) Integers and Number Theory (21) Whole Numbers and Their Operations (18) |
| LDM | Numeration and Computation (21) Decimals, Real Numbers, and Proportional Reasoning (21) Measurement: Length, Area, and Volume (16) |
| MBP | Whole-Number Computation–Mental, Electronic, and Written (80) Rational Numbers, Real Numbers, and Algebra (64) |
| SSN | Representing and Interpreting Data with One Variable (32) Understanding Change: Relationships among Time, Distance, and Rate (12) |
The six textbooks varied in their presentation of technology as it relates to mathematical topics, yet some patterns we noted are described in Table 2. The three textbooks with the largest number of references (MBP, BLL, and LDM) all emphasized the use of technology within chapters related to computation with decimals and real numbers. These references primarily appeared in the textbook with instructions for how to use a calculator to perform a certain task, followed later by activities requesting the use of a calculator for a similar task. Use of technology in other content areas, such as probability and statistics, varied from book to book. Probability and Statistics was the primary location for technology references in SSN, but the topic received less attention in the other textbooks. Within SSN, chapters focusing on topics in geometry had no technology references at all, while all of the geometry chapters in LDM and MBP had at least one technology reference. All six books in the sample contained multiple chapters related to geometry, and at least one technology reference was related to geometry in each textbook.
Some textbooks contained appendices that referenced technology in their titles. Specifically, both LDM and SSN contained an appendix with instructions for using calculators and Geometer’s Sketchpad. SSN also contained appendices for using Fathom (Finzer, 2002), Excel, or the NCTM Illuminations website. We did not examine the content of these appendices. Additionally, each of these textbooks has a companion website, available to the purchaser. We did identify and code references to these companion websites, but we did not analyze the contents of the website.
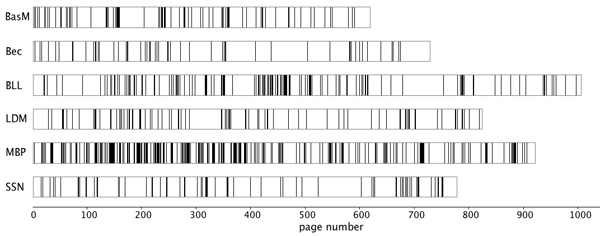
The location of each technology reference within each textbook was coded using page numbers. The first page of each textbook was numbered 1, but each textbook contained a different number of pages. Figure 1 provides a display of the distribution of pages that contained technology references within the six textbooks in our sample. The length of each rectangle represents the set of chapter pages in each book, and the vertical line segments are aligned with page number for each reference.
Nearly three fourths of the technology references occurred in activities, problem sets, or exercises and were coded as activity; over half of these required the use of technology. About one seventh of the tasks were coded as main, and about one ninth of them were coded as auxiliary. These results are displayed by textbook in Figure 2.

As shown in Figure 2, the locations of technology references varied considerably across the textbooks. Five of the six textbooks included sidebars or specially-marked sections, and technology references in these locations were coded as Auxiliary. While SSN did not utilize this feature, almost half of the technology references in BLL were located in sections titled “Technology Corner,” and both Bec and MBP frequently referred to websites within sidebars.
The majority of technology references were contained in activities in each textbook, with the exception of BLL. Within the set of references coded as activity, we found considerable variation of the level to which technology was required. In BasM, for example, technology references in activities were most often coded as reference only, meaning that technology was mentioned within the activity but was not necessarily used. This code was commonly used when a URL was used to cite the source of a dataset.
Within Bec and SSN, a similar numbers of references were found within activities where technology was required and activities where technology was mentioned as an option. The LDM and MBP textbooks sometimes used icons to imply the use of technology; within LDM, nearly as many activities implied the use of technology as required technology. Finally, within MBP, nearly two thirds of the references that occurred within activities required the use of technology.
Role of Technology
We coded each reference according to the role of technology: mathematical action technologies, conveyance technologies (Dick & Hollebrands, 2011), and term. Figure 3 contains the counts of tasks coded within each category. The majority of references in each book were mathematical action technologies, ranging from 51% in BasM to 97% of the references in LDM. The textbooks with fewer numbers of references overall (Bec, BasM, and SSN) had larger proportions of conveyance technologies.
In Bec, over one third of the references were coded as conveyance technologies; these were primarily websites that contained videos of children doing mathematics. BasM had the largest proportion of technology references coded as term. In some cases, the authors were speaking about technology, such as, “We also use metric prefixes when we describe the memory on our computers…” (BasM, p. 511). In other cases, technology was included in the context of a problem, as in “Julie is working out on a computerized ski machine…” (BasM, p. 155). In these cases, it was difficult to clearly determine whether the particular technology (such as computer) had a role of mathematical action or conveyance. Hence, all such references were coded as terms.

Types of Technology
Twelve types of technology were identified within these references and are listed and described in Table 3. The first 10 types are listed in order of relative frequency for the entire set of 1,055 references across the six textbooks; the final two categories are “unspecified technology” and “other technology.” In Table 4 the number of references of each type of technology is listed for each textbook in the sample.
Table 3
Description of Types of Technology Referenced in Textbooks
| Type of Technology | Description |
| Calculator | A generic description for a handheld device that can perform operations with whole numbers, fractions, decimals, integers, and real numbers |
| Website | An electronic resource available online, which may include content provided by the publisher, or links to other sites, such as the National Library of Virtual Manipulatives, NCTM Illuminations website, and IMAP videos |
| E-manipulative | An electronic manipulative provided by the textbook publisher for a specific activity or set of activities |
| Dynamic geometry software | Computer software that allows for the construction and measurement of geometric objects; such as Geometer’s Sketchpad and GeoGebra |
| Computer | An electronic device used to run programs or software, conduct simulations, and access the internet |
| Spreadsheet | Computer software designed to facilitate the organizing and representing data, conduct simulations, or use formulas to create and investigate patterns; such as Excel |
| Graphing calculator | A handheld device that can perform the functions of a calculator and also allow the user to construct graphs, write programs, and organize and represent data |
| Internet | A label utilized when the reference mentioned the internet (or “the web”), but did not provide a specific website or URL |
| Motion detector | A device that uses sound waves and software to produce graphical representations of distance, velocity, and acceleration vs. time |
| Dynamic statistics software | Computer software used to represent data, simulate experiments, and calculate measures of center and variation; such as Fathom |
| Unspecified technology | A label utilized when the reference included phrasing similar to “use some sort of technology” or “ use appropriate technology” |
| Other technology | Specified technologies that were mentioned once, including adding machine, cathode ray tube, computerized ski machine, database, e-mail, e-textbook, electronic financial transaction, and video; iPods (mentioned four times) were also included here |
Table 4
Number (and Percentage) of Types of Technology Referenced in Textbooks
| Type of Technology | Book | |||||
| BasM | Bec | BLL | LDM | MBP | SSN | |
| Calculator | 25 (27%) | 25 (35%) | 81 (48%) | 101 (66%) | 199 (44%) | 22 (18%) |
| Website | 37 (40%) | 35 (49%) | 12 (7%) | 0 | 51 (11%) | 42 (35%) |
| E-manipulative | 0 | 0 | 14 (8%) | 0 | 140 (31%) | 0 |
| Dynamic geometry software | 4 (4%) | 10 (14%) | 23 (14%) | 28 (18%) | 20 (4%) | 0 |
| Computer | 12 (13%) | 0 | 10 (6%) | 5 (3%) | 22 (5%) | 16 (13%) |
| Spreadsheet | 3 (3%) | 0 | 21 (12%) | 4 (3%) | 3 (1%) | 4 (3%) |
| Graphing calculator | 0 | 0 | 3 (2%) | 12 (8%) | 11 (2%) | 1 (1%) |
| Internet | 8 (9%) | 1 (1%) | 2 (1%) | 0 | 0 | 1 (1%) |
| Motion detector | 0 | 0 | 0 | 0 | 0 | 9 (8%) |
| Dynamic statistics software | 0 | 0 | 0 | 0 | 0 | 4 (3%) |
| Unspecified technology | 1 (1%) | 0 | 3 (2%) | 1 (1%) | 2 (1%) | 15 (13%) |
| Other technology | 3 (3%) | 0 | 0 | 1 (1%) | 3 (1%) | 5 (4%) |
| Note: Percentages for a single book (i.e., for each column) may not sum to 100 due to rounding. | ||||||
Table 4 shows the variation within the primary the types of technology contained within the textbooks. Calculators were the most common type referenced in LDM, BLL, and MBP, while websites were most frequent within Bec, BasM, and SSN. MBP contained a large number of e-manipulatives, which are similar to some of the websites referenced in other textbooks, but are housed on the publisher’s website. With this approach, the authors of MBP did not need to rely on the stability of external websites. Finally, all of the textbooks except for SSN made explicit references to dynamic geometry software, which is particularly intriguing because SSN contained an appendix focusing on using Geometer’s Sketchpad.
Summary of the Treatment of Technology Within Each Textbook
This section includes a brief summary of the treatment of technology within each textbook and a table with the total number of references to mathematical action technologies according to type of technology. These references are then further refined to the number of mathematical action technologies contained in activities that were required, implied, or optional.
BasM. At multiple points within each section, the authors of BasM encouraged the reader to stop and think about a situation, as prospective teachers will “learn those ideas more deeply than if they are simply presented with the concepts via lecture and then are given problems for practice.” (p. xii). In addition to Investigations laced throughout the main text, this book has a companion Explorations Manual. We analyzed the sixth edition of this textbook, which included, “more technology, including references to virtual manipulatives, Geogebra [sic] investigations, and several other websites” (p. viii) compared to the previous edition.
We identified 93 references to technology, with 47 classified as mathematical action technologies. Table 5 shows that calculators were a prominent technology referenced within BasM. Most of the calculator references occurred within the main section of the text, although five references were within activities that required calculator use. Websites were the most common type of technology required within activities. Typically, these websites provided virtual manipulatives and activities, such as the National Library of Virtual Manipulatives (http://nlvm.usu.edu), NCTM Illuminations (http://illuminations.nctm.org), and Shodor Interactiviate (http://www.shodor.org/interactivate).
Table 5
Counts of Technology References Within BasM, Bec, and BLL
Type of Technology | Mathematical Action Total | Mathematical Action and Activity-Required | Mathematical Action and Activity-Optional |
| BasM | |||
| Calculator | 25 | 5 | 0 |
| Website | 14 | 11 | 1 |
| Dynamic geometry software | 4 | 1 | 1 |
| Spreadsheet | 3 | 0 | 0 |
| Computer | 1 | 0 | 0 |
| Bec | |||
| Calculator | 25 | 12 | 0 |
| Dynamic geometry software | 10 | 0 | 3 |
| Website | 9 | 4 | 5 |
| BLL | |||
| Calculator | 68 | 17 | 4 |
| Dynamic geometry software | 23 | 0 | 5 |
| Spreadsheet | 21 | 1 | 0 |
| E-manipulative | 14 | 0 | 0 |
| Graphing calculator | 3 | 0 | 0 |
| Internet | 1 | 1 | 0 |
| Unspecified technology | 3 | 0 | 2 |
BasM included references to GeoGebra and spreadsheets, but they primarily occurred within discussion in the main section of the text. Like many calculator references, the authors discussed how and when such technology could be used but provided relatively few activities where the use of technology was required or explicitly presented as an option.
Bec. In the preface, the author stated her overarching goal, “To teach mathematics well teachers must know more than how to carry out basic mathematical procedures; they must be able to explain why mathematics works the way it does.” (Bec, p. xii, emphasis in original). To that end, she wove class activities and links to the Integrating Mathematics and Pedagogy (IMAP) videos (http://www.sci.sdsu.edu/CRMSE/IMAP/video.html) designed to do just that. While the book contained the standard exposition of mathematical ideas, it also included places where students (and the instructor) should stop and think about the material being presented.
Of the 71 references to technology in Bec, 44 referred to mathematical action technologies. As show in Table 5, these references related to calculators, dynamic geometry software, and websites. Almost half of the calculator references were within Activities, and the use of a calculator was required.
In chapters related to geometry were references to dynamic geometry software; in sections involving transformations, three activities provided an option for using dynamic geometry software. As with BasM, the website references coded as mathematical action technologies referred to virtual manipulatives (e.g., NCTM Illuminations).
One notable and unique feature of the Bec textbook is that the class activities were included as part of the textbook in a section that follows the main section. Many textbooks of this type come with a student activity manual under a separate cover. References to specific class activities were contained in the main flow of the chapter or section, as opposed to a sidebar comment. The author clearly intended these activities to be a significant part of material covered in class.
BLL. In the preface of this textbook, the authors wrote, “This [10th] edition continues to be heavily concept- and skill-based, with new emphasis on active and collaborative learning.” (p. vii). Thus, the authors attempted to interlace active and collaborative learning activities on top of the previously existing main content. Student activities were added to each section, but references to the activities usually occurred in a sidebar and assumed students also had the activity manual. The material can be covered without using the activities, however.
We found 169 references to technology in this text, and 133 were mathematical action technologies. There was a strong emphasis on calculators, but also multiple references to dynamic geometry software and spreadsheets (see Table 5). Calculator references tended to appear in the sections on number and operation, dynamic geometry software in sections involving transformations, and spreadsheet references spread among statistics and number and operations. Most of the references were not located within activities. Instead, the references appeared within the main text or text boxes with the title, “Technology Corner.” This book referenced some e-manipulatives available in a companion CD, but none of these manipulatives were required for activities.
The single Internet reference coded as mathematical action required the reader to use Internet search engines and experiment with the use of Boolean operators “and” and “or.” The two references coded as “unspecified technology” occurred when readers were encouraged to use some method of generating random numbers.
The book maintained a heavy focus on skill development, especially in the numerous exercise problems at the end of each section. However, problem sets included sections on communication, cooperative learning, classroom questions, open-ended questions, and review questions from previous sections.
LDM. Within the preface, the authors note that they stress problem-solving throughout the textbook with an emphasis placed on the mathematical knowledge prospective teachers need for teaching. Further, problem solving “continues not only in the discussion of the various topics, but, perhaps even more importantly, in virtually all sections of the problem sets.” (LDM, p. xiii). Designed to engage the student in thoughtful mathematics, the text has an abundance of activities, investigations, and problems that may require multiple steps and reflection.
We identified 152 technology references, and nearly all of them (148) were mathematical action technologies. The majority of these referred to calculators; however, there were also references to dynamic geometry software and spreadsheets. Table 6 lists all of the mathematical action technologies referenced in LDM.
Some activities within this textbook were marked with a special icon to imply the use of technology. Almost half of the calculator references (48 of 99) were of this type. When dynamic geometry software is mentioned, it is often required to complete a mathematical activity. The textbook often refers to geometry software in a generic sense, but does contain an appendix with instructions for using Geometer’s Sketchpad. There is also an appendix with instructions for using spreadsheets.
Table 6
Counts of Technology References Within LDM and MBP
Type of Technology | Mathematical Action Total | Mathematical Action and Activity-Required | Mathematical Action and Activity- Implied | Mathematical Action and Activity-Optional |
| LDM | ||||
| Calculator | 99 | 31 | 48 | 1 |
| Dynamic geometry software | 28 | 22 | 4 | 0 |
| Graphing calculator | 12 | 5 | 1 | 0 |
| Computer | 4 | 0 | 0 | 0 |
| Spreadsheet | 4 | 0 | 0 | 2 |
| Unspecified technology | 1 | 0 | 0 | 0 |
| MBP | ||||
| Calculator | 199 | 77 | 38 | 20 |
| E-manipulative | 140 | 103 | 1 | 36 |
| Dynamic geometry software | 20 | 20 | 0 | 0 |
| Computer | 18 | 0 | 0 | 0 |
| Graphing calculator | 11 | 1 | 0 | 9 |
| Spreadsheet | 3 | 3 | 0 | 0 |
| Unspecified technology | 1 | 0 | 0 | 0 |
| Other technology | 1 | 0 | 0 | 0 |
The reference classified as “unspecified technology” in LDM occurred at the introduction to the statistics chapter, where statistical software is mentioned as one of several technologies that are used in data analysis.
MBP. In the preface of MBP, the authors list three underlying themes for the book: problem solving, deductive reasoning, and technology. Referring to this third theme, “Various forms of technology are an integral part of society and can enrich the mathematical understanding of students when used appropriately” (MBP, p. xii). These references to technology are located in many parts of the book: within both the main text and activities, and at times optional or implied, but most frequently required.
We identified 451 technology references in MBP, and 393 were coded as mathematical action technologies. Of these, over half (199) referred to calculators (see Table 6). As with LDM, certain activities in MBP were marked with an icon that implied the use of technology. A unique feature of this book was the inclusion of a large number of e-manipulatives; these were available on the book’s companion website and often required when they were mentioned within activities. These e-manipulatives were integrated within various content areas: number and operation, geometry, and statistics and probability.
The reference coded as “unspecified technology” was located in a sidebar and mentioned the role of technology in the workplace to perform lower order tasks such as computation. The “other technology” referred to an adding machine, contained in a historical discussion of computational devices.
SSN. In the preface, the authors posit that “mathematics is not just about getting answers to questions but rather about developing insight into mathematical relationships and structures” (SSN, p. xiii). From this perspective, the authors sequence activities, discussions, and questions throughout the main portion of the text. The book is divided into four major parts. The greatest number of technology references were found in the final part, which focused on statistics and probability.
We identified 119 technology references, with 96 of them coded as mathematical action technologies. As shown in Table 7, the most common type of technology was in the form of a website, such as the NCTM Illuminations. Almost all of these website references were located within activities; half of these required the use of a website, and in the other half the use was optional. Calculators were mentioned in the main text, but occurred less frequently in activities.
Table 7
Counts of Technology References Within SSN
Type of Technology | Mathematical Action Total | Mathematical Action and Activity-Required | Mathematical Action and Activity-Optional |
| Website | 26 | 12 | 12 |
| Calculator | 22 | 2 | 5 |
| Computer | 13 | 1 | 1 |
| Motion detector | 9 | 3 | 0 |
| Spreadsheet | 4 | 0 | 0 |
| Dynamic statistics software | 4 | 1 | 3 |
| Unspecified technology | 15 | 6 | 3 |
This textbook was unique within our sample, in that it used motion detectors; these references occurred exclusively within a single chapter, entitled “Understanding Change: Relationships Among Time, Distance, and Rate.” This text also incorporated dynamic statistics software, namely Fathom. Most of the “unspecified technology” references required the reader to select a form of technology, with instructions similar to, “Use appropriate technology to complete this task.”
This book also includes appendices with technology content: links to videos of students doing mathematics, instructions for using technology such Geometer’s Sketchpad, the TI-73 calculator, Fathom, Excel, or the NCTM Illuminations website.
References That Impact TPACK
In order to develop TPACK within prospective elementary teachers, textbooks may provide multiple opportunities that utilize different types of technology across all areas of mathematics. Some tools, such as calculators, graphing calculators, and spreadsheets, are widely available and can be used for a number of diverse mathematical topics. Other types of technology are more specialized, such as dynamic geometry software or online resources. These, along with customized e-manipulatives like dynamic geoboards, can be used for specific tasks.
When technology is incorporated in a mathematics content course, prospective teachers’ technological content knowledge (TCK) and technological pedagogical knowledge (TPK) may be impacted. Koehler and Mishra (2008) define TCK as, “an understanding of the manner in which technology and content influence and constrain one another” (p. 16), while TPK is, “an understanding of how teaching and learning changes when particular technologies are used” (p. 16). Prospective teachers may also develop TPACK, which is, “an understanding that emerges from the interaction of content, pedagogy, and technology knowledge” (p. 17, emphasis in original). We searched the literature on TPACK development, but found no studies or recommendations related to the content of textbooks. On the other hand, there were abundant examples of activities and experiences designed to impact the development of TPACK (e.g., AACTE Committee on Innovation and Technology, 2008; Niess et al., 2009). After reviewing these, we created a list of features of technology references within mathematics textbooks that have the potential to impact a prospective elementary teacher’s TPACK. This list is not exhaustive, but provides a few examples that may be present in technology references. Namely, these references:
- Highlight the inclusion and use of technology within mathematics curriculum materials;
- Describe or discuss the reason(s) for choosing to use, or not use, particular types of technology within the context of teaching mathematics;
- Require prospective teachers to explain, in a manner that a student could understand, the output of various types of technology;
- Illustrate students’ use of technology, using video or descriptions of student work;
- Make explicit statements about, or provide examples of, how technology may be used in the school classroom.
These examples, while not prevalent within the textbooks, were nonetheless present in some of the references to technology. If the goal is to prepare teachers to use technology in their future classrooms, such features should be emphasized on an even greater scale. In the following section are some examples from each textbook that contain some of these features and, thus, have the potential to impact the development of TPACK in a prospective elementary teacher.
Highlight Technology in Curriculum Materials. Most of the textbooks in our sample included pictures of pages from textbooks used in elementary schools. For example, MBP includes a picture of a page from a fourth-grade textbook (MBP, p. 155). On this page, there is a “Math Online” sidebar that lists the publisher’s website and the resources that are available, such as extra examples, activities, and video tutorials. Within BLL, the authors included a “School Book Page: Learning with Technology” subsection containing a portion of a sixth-grade textbook (BLL, p. 202). Within this page, sixth-grade students are introduced to the Fibonacci sequence and required to use a spreadsheet to investigate the sequence.
Describe Reasons for Selecting Technology. In a chapter on statistics in SSN, after discussing simulations and sampling methods, the authors stated,
When statisticians want to find a random sample, they do not usually draw names from a hat, spin a spinner, or toss a die, although these are legitimate ways to sample randomly. To obtain a large sample, these methods would be very time-consuming. Instead, statisticians might use computer simulation software, a table of random numbers, or a computer or calculator with the capability of providing random numbers. (SSN, p. 667)
Therefore, one reason for choosing to use technology is because of the speed at which technology can perform complex or repetitive tasks. On the other hand, in a chapter on operations, the authors of BasM provide a rationale for choosing to not use technology for certain tasks:
Our first work with addition in base ten will be doing some addition problems mentally, for a couple of reasons. First, this will require you to think carefully about how your knowledge of place value applies to adding numbers. Second, much of our use of arithmetic does not involve pencil and paper or calculators, but rather mental computation—when estimating or when it is quicker to do a computation or part of a computation in our head than with a pencil or calculators (BasM, p. 81).
With this statement, the authors indicated that there are good reasons to choose to use – or not to use – technology in certain situations. Later, in a section on operations with decimals, they made the following statement in support of using calculators.
With the widespread use of calculators, most people no longer do most decimal computations longhand. However, it is crucial to understand why the basic algorithms work because it is often necessary to interpret what the calculator displays. (p. 231)
Thus, the authors of BasM recommended the use of calculators be coupled with a conceptual understanding of number and operations.
We found some technology references in which prospective teachers were asked to compare the merits of different types of technology. For example, the authors of BLL included this prompt within an exercise set: “A student questions whether a spreadsheet or a graphing calculator is more useful to teach algebra concepts. How do you respond?” (BLL, p. 471).
Require Explanations of the Output of Technology. Some tasks placed the prospective teachers in situations that they will likely face when using technology in the classroom. For example, consider the situation presented in Bec:
Ron used a calculator to determine that 0.35 × 2.4 = 0.84. Ron wants to know why the rule about adding up the number of places to the right of the decimal doesn’t work in this case. Why aren’t there 2 + 1 = 3 digits to the right of the decimal point in the answer? Is Ron correct that the rule about adding the number of places to the right of the decimal points is not correct in this case? Explain. (Bec, p. 207)
A similar activity in SSN also referenced calculators:
A student says, “My calculator shows that [the square root of 2] is 1.4142136. And 1.4142136 = [14,142,136/10,000,000], which is a rational number. But you said [the square root of 2] is an irrational number. Which is it, rational or irrational?” How would you respond to the student? (SSN, p. 119)
Specifically, these activities require an understanding of how one must thoughtfully interpret the output of a calculator and explain that output to a student.
Illustrate Students’ Use of Technology. Each of the textbooks in our sample provided instructions for using technology in various mathematical tasks, but the examples were primarily instructive to the reader as a user of technology. We did not identify any descriptions of elementary students’ interactions with technology beyond instances similar to the examples given in the previous section. Although some textbooks included references to videos of students doing mathematics, none of the videos incorporated technology.
Explicitly Describe the Use of Technology in Schools. The authors of LDM illustrated the benefits of using dynamic geometry software for making a geometric constructions more enjoyable and less tedious:
Constructions made with tangible materials – paper, dowels, rubber bands, and so on – continue to have an important role to play in teaching and learning the principles of geometry. However, increasingly, classrooms are also taking advantage of the computer. Geometry software…allows figures to be constructed on the screen, colored, manipulated, explored with measurement tools, and printed out for display and further investigation. (LDM, p. 684)
In a section entitled, “Mental Math, Estimation, and Calculators,” the authors of MBP described a specific calculator:
The TI-34 II, which is designed especially for elementary and middle schools, performs fraction as well as the usual decimal calculations, can perform long division with remainders directly, and has the functions of a scientific calculator. One nice feature of the TI-34 II is that it has two lines of display, which allows the student to see the input and output at the same time. (MBP, p. 141)
Adjacent to this paragraph on the page, there is a sidebar citing Reys and Reys (1987), who listed benefits of calculator use in the classroom, such as a more positive attitude toward mathematics.
These examples are provided to demonstrate how textbooks may provide opportunities for prospective teachers to develop TPACK. However, the instructor has a great influence on how a textbook is used within a course. In the next section are recommendations for textbook selection, curriculum development, and future research directions based on our research.
Recommendations
Textbook Selection
Not all mathematics textbooks for prospective elementary teachers are the same. This study highlights the variation in the extent and nature of the use of technology in teaching and learning mathematics. It is important to note that these findings provide a description, but not an evaluation, of the textbooks in the sample. The goals of the course, the role of technology, and the availability of technological resources must be considered when selecting and implementing a textbook.
Any content analysis of a textbook should also be viewed in light of the fact that textbooks are not self-implementing. In any course, the instructor will naturally choose to implement some portions of a textbook, omit others, and possibly use other resources that are not in the textbook. In this paper, we have provided an overview of how an instructor can make informed decisions about the amount and type of technology to be used in a course. The instructor should find our categorization of technology by its location, type, and role a useful starting point when considering how to implement the content of the textbook. Beyond knowing the types of technology that can be found in a textbook, information related to the location and role of the technology can affect the instructor’s choice of how to impact students’ learning and, in some cases (such as the example from p. 471 of BLL earlier in this paper) impact students’ understanding of the role of technology in the learning of mathematics.
The textbook is a potentially influential component of a mathematics content course for prospective teachers, but the presence or absence of technology references within a textbook does not necessarily indicate the presence or absence of technology within the course. With respect to a mathematics teacher education program, it is beneficial to have technology represented within content courses. Content courses that include, highlight, and discuss technology fit with the characteristics of mathematics teacher preparation programs that strive to develop a strong TPACK foundation within their teacher candidates. “A successful program would probably not overly separate technology, content, and pedagogy across the coursework of teachers. In other words, the required courses within the mathematics department would include strong technology use and effective pedagogy of presentation,” (Grandgenett, 2008, p. 161). As Niess and colleagues (2009) noted, individuals progress through a series of levels as they develop TPACK. By selecting a textbook that incorporates technology within a content course, instructors may help prospective teachers progress through the initial stages of Recognizing and Accepting, particularly in the themes of Curriculum and Assessment, Learning, and Access.
One limitation of our work lies in the challenge to identify all of the references to technology within each textbook of our sample. While we were diligent in examining every page, each textbook in our sample contained hundreds of pages of content. Therefore, it is possible that we missed some references. Another limitation arises because the use of technology within an activity was not necessarily clear cut. For example, while an author and instructor may intend for a student to use a calculator to compute 76 with a calculator, we did not include such an activity in our analysis unless a calculator was specifically mentioned or a special icon was present. Therefore, in some sense, our counts provide a floor for the level of technology integration for each of these books.
As we mentioned earlier, another limitation of our study is that two textbooks in our sample (BLL and MBP) are not the most current editions available. In fact, according to the publisher’s website for MBP (John Wiley & Sons, Inc., 2016), the latest edition includes QR codes and new videos of children solving mathematics problems. This new content would have been included in our analysis, had we examined this edition. Therefore, instructors of mathematics courses for prospective elementary teachers should regularly review new editions of textbooks, as a review of new features will provide useful information for the textbook selection process.
Curriculum Development
Textbook authors must naturally wrestle with the question, “What technologies may we assume students and instructors may access and use?” In academic institutions in the U.S., it may be the case that all students have access to computer labs and the internet. Furthermore, the low cost of calculators, or their availability inside the classroom, (or their automatic inclusion among the apps of a smartphone) may allow textbook authors to design tasks that utilize such resources without worries that not all students may have access. Even as technology advances, this question must be addressed.
Within a teacher preparation program, prospective elementary teachers need opportunities to (1) learn how to use specific types of technology for learning mathematics (ISTE, 2008), (2) observe how technology is used to teach mathematics (AMTE, 2006), (3) practice teaching mathematics with technology (NCTM, 2011), and (4) develop an inclination towards teaching and learning mathematics with technology, including technologies that have not yet been developed (AMTE, 2006; ISTE, 2008; NCTM, 2011). This is quite a tall order for teacher preparation programs, and cooperation must exist alongside content courses, methods courses, and practical field-based experiences.
There are textbooks that emphasize the use of technology for teaching mathematics at the middle and secondary levels, such as those that emerged from the Preparing to Teach Mathematics with Technology Project (Hollebrands & Lee, 2012; Lee, Hollebrands, & Wilson, 2010). Future curriculum development efforts may need to focus on teaching and learning mathematics content from the elementary level. Furthermore, recent developments in online curriculum materials and e-textbooks may lead the way for the seamless integration of technology tools and mathematics tasks.
Overall, we recommend that new textbooks, and new editions of existing textbooks, attend to the features of tasks that potentially impact a prospective teacher’s TPACK. In particular, we encourage authors to utilize videos that illustrate students’ use of technology in the elementary classroom. The authors of MBP have shown that adding videos to a new edition of the textbook is feasible (John Wiley & Sons, Inc., 2016); we recommend that some of these videos include students interacting with electronic technology to solve mathematics problems.
Future Research Directions
Several avenues exist for future research along these lines. First of all, while this study examined many of the popular textbooks for this type of course, other textbooks exist. It would be interesting to see if other textbooks are similar to those in our sample, or if even more variation exists. One interesting branch of research in this vein involves comparing U.S. textbooks to textbooks used in courses for prospective elementary teachers in other countries.
Second, many current textbooks have been through multiple revisions. It may be interesting to look at previous editions of these textbooks and see how they have evolved along with technology. For example, what types of technology were mentioned in the first editions of such textbooks, and how do those correspond with the advent of various types of technology? A quick glance at an earlier edition of LDM revealed a section titled, “Getting the Most Out of Your Calculator,” that has since been eliminated. Perhaps the reasons for such changes would be best gathered by interviewing the authors.
A third direction for future study focuses on the implementation of such textbooks within content courses. That is, if you know an instructor is using a certain textbook, how does the technology mentioned in the textbook actually get used in the class? This would be particularly fascinating in relation to e-textbooks.
Conclusion
This study has revealed that textbooks for mathematics content courses for prospective elementary teachers do contain references to technology, but the presentation of technology varies with the textbook. While it may be the case that teacher preparation programs in the past did not utilize technology, current textbooks do provide some opportunities to learn and teach mathematics with technology, particularly with calculators and online resources. At the same time, mathematics teacher educators must be diligent in effort to prepare teachers to effectively use technology in the mathematics classroom. Taking the perceived problem up a level, mathematics teacher educators may not have learned to teach mathematics with technology during their preparation, either. Further research on the development and implementation of curriculum and its relationship to technology will help steer us toward the goal of teaching mathematics effectively in the digital age.
References
AACTE Committee on Innovation and Technology (Ed.). (2008). Handbook of technological pedagogical content knowledge (TPCK) for educators. New York, NY: Routledge.
Association of Mathematics Teacher Educators. (2006). Preparing teachers to use technology to enhance the learning of mathematics: A position of the Association of Mathematics Teacher Educators. Retrieved from http://amte.net/sites/default/files/amtetechnologypositionstatement.pdf
Bassarear, T., & Moss, M. (2014). Mathematics for elementary school teachers (6th ed.). Boston, MA: Cengage Learning.
Beckmann, S. (2014). Mathematics for elementary teachers with activities (4th ed.). Boston, MA: Pearson.
Bull, G., & Bell, L. (2009). TPACK: A framework for the CITE Journal. Contemporary Issues in Technology and Teacher Education, 9(1). Retrieved from https://citejournal.org/vol9/iss1/editorial/article1.cfm
Billstein, R., Libeskind, S., & Lott, J. W. (2010). A problem solving approach to mathematics for elementary school teachers (10th ed.). Boston, MA: Addison Wesley.
Dick, T. P., & Hollebrands, K. F. (2011). Focus in high school mathematics: Technology to support reasoning and sense making. Reston, VA: National Council of Teachers of Mathematics.
Conference Board of the Mathematical Sciences. (2012). The mathematical education of teachers II. Washington, DC: American Mathematical Society and Mathematical Association of America.
Finzer, W. (2002). Fathom dynamic data software (Version 2.1) [computer software]. Emeryville, CA: Key Curriculum Press.
Grandgenett, N. F. (2008). Perhaps a matter of imagination: TPCK in mathematics education. In AACTE Committee on Innovation and Technology (Ed.), Handbook of technological pedagogical content knowledge (TPCK) for educators (pp. 145-165). New York, NY: Routledge.
Hollebrands, K. F., & Lee, H. S. (2012). Preparing to teach mathematics with technology: An integrated approach to geometry. Dubuque, IA: Kendall Hunt Publishing Company.
International Society for Technology in Education. (2007). ISTE standards for students. Eugene, OR: Author.
International Society for Technology in Education. (2008). ISTE standards for teachers. Eugene, OR: Author.
Jones, D. L. (2014). The role of technology for learning stochastics in U.S. textbooks for prospective teachers. Paper presented at the International Conference on Mathematics Textbook Research and Development, Southampton, United Kingdom.
Koehler, M. J., & Mishra, P. (2008). Introducing TPCK. In AACTE Committee on Innovation and Technology (Ed.), Handbook of technological pedagogical content knowledge (TPCK) for educators (pp. 3-29). New York, NY: Routledge.
Lee, H. S., Hollebrands, K. F., & Wilson, P. H. (2010). Preparing to teach mathematics with technology: An integrated approach to data analysis and probability. Dubuque, IA: Kendall Hunt Publishing Company.
Long, C. T., DeTemple, D. W., & Millman R. S. (2012). Mathematical reasoning for elementary teachers (6th ed.). Boston, MA: Addison Wesley.
McBroom, E. S. (2012). Teaching with dynamic geometry software: A multiple case study of teachers’ technological pedagogical content knowledge (Unpublished doctoral dissertation). Texas State University, San Marcos, TX.
McCrory, R. (2006). Mathematicians and mathematics textbooks for prospective elementary teachers. Notices of the AMS, 53(1), 20-29.
McCrory, R., & Stylianides, A. J. (2014). Reasoning-and-proving in mathematics textbooks for prospective elementary teachers. International Journal of Educational Research, 64, 119-131.
Mishra, P. & Koehler, M. (2006). Technological pedagogical content knowledge: A framework for teacher knowledge. Teachers College Record, 108(6), 1017-1054.
Musser, G. L., Burger, W. F., & Peterson, B. E. (2011). Mathematics for elementary teachers: A contemporary approach (9th ed.). Hoboken, NJ: John Wiley & Sons.
Musser, G. L., Peterson, B.E., & Burger, W.F. (2013). Mathematics for elementary teachers: A contemporary approach (10th ed.). Hoboken, NJ: Wiley & Sons
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. (2011). Technology in teaching and learning mathematics: A position of the National Council of Teachers of Mathematics. Retrieved from http://www.nctm.org/Standards-and-Positions/Position-Statements/Technology-in-Teaching-and-Learning-Mathematics/
National Council on Teacher Quality. (2008). No common denominator: The preparation of elementary teachers in mathematics by America’s education schools. Retrieved from http://www.nctq.org/p/publications/docs/nctq_ttmath_fullreport.pdf
Niess, M. L. (2005). Preparing teachers to teach science and mathematics with technology: Developing a technology pedagogical content knowledge. Teaching and Teacher Education, 21(5), 509-523.
Niess, M. L., Ronau, R. N., Shafer, K. G., Driskell, S. O., Harper S. R., Johnston, C., … & Kersaint, G. (2009). Mathematics teacher TPACK standards and development model. Contemporary Issues in Technology and Teacher Education, 9(1), 4-24. Retrieved from https://citejournal.org/volume-9/issue-1-09/mathematics/mathematics-teacher-tpack-standards-and-development-model
Reys, B. J., & Reys, R. E. (1987). Calculators in the classroom: How can we make it happen? Arithmetic Teacher, 34(6), 12-14.
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4-14.
Sowder, J., Sowder, L., & Nickerson, S. (2014). Reconceptualizing mathematics for elementary school teachers (2nd ed.). New York, NY: W. H. Freeman and Company.
Appendix A
List of Textbooks Examined and Abbreviations
BasM – Bassarear and Moss (2014). Mathematics for Elementary School Teachers, 6th edition
Bec – Beckmann (2014). Mathematics for Elementary Teachers with Activities, 4th edition
BLL – Billstein, Libeskind, and Lott (2010). A Problem Solving Approach to Mathematics for Elementary School Teachers, 10th edition
LDM – Long, DeTemple, and Millman (2012). Mathematical Reasoning for Elementary Teachers, 6th edition
MBP – Musser, Burger, and Peterson (2011). Mathematics for Elementary Teachers: A Contemporary Approach, 9th edition
SSN – Sowder, Sowder, and Nickerson (2014). Reconceptualizing Mathematics for Elementary School Teachers, 2nd edition
Appendix B
Codes and Example References
| Code | Definition | Example |
| Required | The textbook explicitly indicates that the use of a particular type of technology should be used to complete the activity. | Go to www.shodor.org/interactivate/ activities/Coin and simulate tossing a coin 1000 times. (BasM, p. 410) |
| Implied | There is no mention of a type of technology, but a special technology icon is present beside the activity, or the preceding chapter indicates that technology should be used to complete the activity. | [A calculator icon precedes this text.] Determine whether the following equation is true for n = 1, 2, or 3. 1n + 6n +8n = 2n +4n +9n (MBP, p. 145) |
| Optional | The textbook suggests the use of technology to complete the activity, along with an option of not using technology. | Investigate the following questions, either with Geometer’s Sketchpad or by making drawings on (graph) paper. (Bec, p. 605) |
| Referenced only | The activity contains a reference to technology, but no technology is needed to complete the activity. This includes citing the source of a dataset with a URL. | Using a calculator, Ralph multiplied by 10 when he should have divided by 10. The display read 300. What should the correct answer be? (BLL, p. 173) |
![]()